跳表是一个随机化的数据结构,可以被看做二叉树的一个变种,它在性能上和红黑树,AVL树不相上下,但是跳表的原理非常简单,目前在Redis和LeveIDB中都有用到。
它采用随机技术决定链表中哪些节点应增加向前指针以及在该节点中应增加多少个指针。跳表结构的头节点需有足够的指针域,以满足可能构造最大级数的需要,而尾节点不需要指针域。
采用这种随机技术,跳表中的搜索、插入、删除操作的时间均为O(logn),然而,最坏情况下时间复杂性却变成O(n)。相比之下,在一个有序数组或链表中进行插入/删除操作的时间为O(n),最坏情况下为O(n)。
跳表的原理非常简单,跳表其实就是一种可以进行二分查找的有序链表。跳表的数据结构模型如图
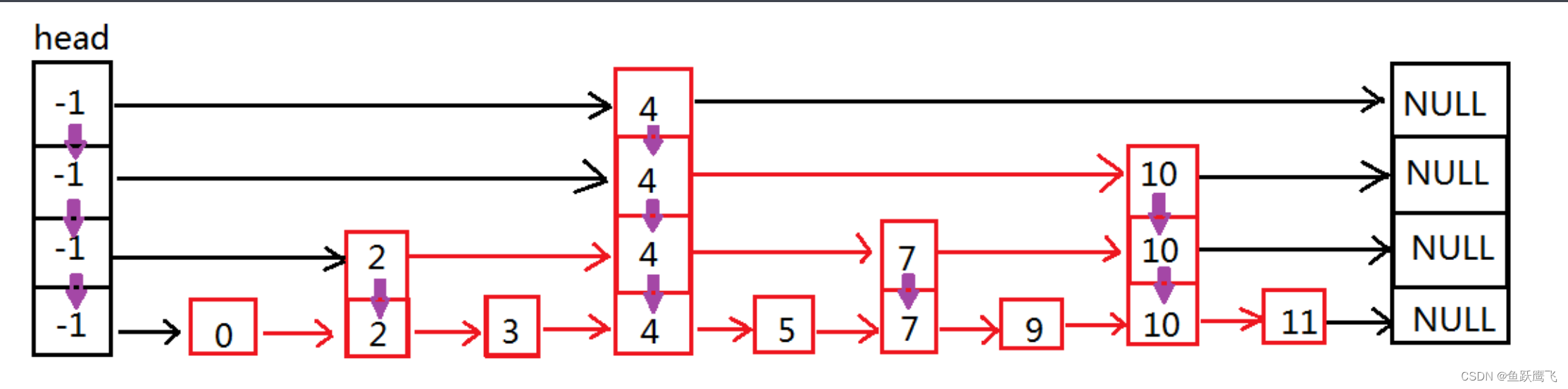
可以看到,跳表在原有的有序链表上面增加了多级索引,通过索引来实现快速查找。首先在最高级索引上查找最后一个小于当前查找元素的位置,然后再跳到次高级索引继续查找,直到跳到最底层为止,这时候以及十分接近要查找的元素的位置了(如果查找元素存在的话)。由于根据索引可以一次跳过多个元素,所以跳查找的查找速度也就变快了。
说了这么多,你可能觉得也不知道跳表到底有啥重要性,我这么说吧:如果面试考redis,问到底层数据结构,跳表是必须要问的,几乎100%的概率,想想你要是能当场给面试官写一个出来,是不是能给他干懵了
那我们就手写一个出来吧:
1.表头元素是一个key和value都为空的节点,不参与任何计算的过程,只用于从开始进行查找
2.让所有的节点的加入所拥有的层次都是随机的,我们这里使用类似于抛硬币的方法,如果Math.random()<0.5就+1,一直到不再小于0.5为止
3.不管什么时候查找某个key(不确定层数的情况下)都从最高层往0层进行查找,每次查当前层比它小的最右边的元素,如果这个元素在当前层的next是它则找到,不然继续查找下一层。
4.删除的时候如果当前的层删除之后只剩head了,那没必要留着了。
package dataStructure.TreeMap;
import java.util.ArrayList;
//跳表节点类
class SkipListNode<K extends Comparable<K>, V> {
public K key;
public V value;
//当前节点的next节点组成的arrayList,有多少层就有多少个节点
public ArrayList<SkipListNode<K, V>> nextNodes;
public SkipListNode(K key, V value) {
this.key = key;
this.value = value;
this.nextNodes = new ArrayList<>();
}
public boolean isKeyLessThan(K otherKey) {
return key != null && otherKey != null && key.compareTo(otherKey) < 0;
}
public boolean isKeyEqualsTo(K otherKey) {
return (key == null && otherKey == null) || (key != null && otherKey != null && key.compareTo(otherKey) == 0);
}
}
public class SkipListMap<K extends Comparable<K>, V > {
//调表的最大层数
private int maxLevel;
//跳表中节点的个数
private int size;
//跳表的头节点,key和value都是null,head的层数和最大层数相同
private SkipListNode<K, V> head;
//随机概率,类似抛硬币
private static final double PROBABILITY = 0.5;
public SkipListMap() {
//初始化一个key和value都为空的节点作为头节点,个人觉得也可以直接放在head声明的地方
head = new SkipListNode<>(null, null);
//最大的层级,我们这里的层级从0开始
maxLevel = 0;
//头节点的nextNodes增加一个空的执行
head.nextNodes.add(null);
size = 0;
}
/**
* 最最高层maxLevel开始一直找到最底层
* 最后一定是在第0层的小于key的最右边的节点
* @param key
* @return
*/
public SkipListNode mostRightLessNodeInTree(K key) {
if(key == null) return null;
int level = maxLevel;
SkipListNode<K, V> node = head;
while(level >= 0) {
node = mostRightLessNodeInLevel(key, node, level --);
}
return node;
}
/**
* 获得curLevel层中小于cur节点的最右边的节点
* @param key 目标节点的key(我们要找比他小的最右边的节点)
* @param cur 这一层中从cur开始找
* @param curLevel 当前所在的层
* @return
*/
private SkipListNode<K ,V> mostRightLessNodeInLevel(K key, SkipListNode<K,V> cur, int curLevel) {
//因为可能右很多层,nextNodes.get(i)代表第i层中next的后继节点
SkipListNode<K, V> next = cur.nextNodes.get(curLevel);
//如果next不为空并且next小于目标key的值就一直继续
//退出条件1:next为空,代表本层最后一个节点,本层所有节点都小于目标节点的key
//推出条件2:next不再小于目标节点的key
while(next != null && next.isKeyLessThan(key)) {
cur = next;
next = cur.nextNodes.get(curLevel);
}
//根据退出条件我们知道cur是当前层中小于目标的key的最右边的节点
//因为next为null的时候没有null已经不是节点了,而next不再小于目标节点的时候,cur是最后一个小于目标key的节点
return cur;
}
/**
* 是否包含某个key为key的节点
* @param key
* @return
*/
public boolean containsKey(K key) {
//要查找的是null,就别找了,没有
if(key == null) return false;
//从最高层依次查找找到第0层的小于key的最右边的节点
SkipListNode<K,V> less = mostRightLessNodeInTree(key);
//如果key是存在于这个跳表里的,那less在第0行的下一个节点肯定是以key为key的
return less.nextNodes.get(0) == null? false : less.nextNodes.get(0).isKeyEqualsTo(key);
}
public K firstKey() {
return head.nextNodes.get(0) == null? null : head.nextNodes.get(0).key;
}
/**
* 获取整个跳表中的最后一个节点,这里一定要从最高层遍历
* 这样的时间复杂度是logN,如果从第0层开始依次往后遍历着找最后一个的话就是O(N)的时间复杂度了
* @return
*/
public K lastKey() {
int level = maxLevel;
SkipListNode<K, V> cur = head;
//从最高层开始每次找到最后的节点
while(level >= 0) {
SkipListNode<K, V> next = cur.nextNodes.get(level);
//本层直到找到next为null为止,cur就是本层最后一个节点
while(next != null) {
cur = next;
next = cur.nextNodes.get(level);
}
//找下一层
level--;
}
//出这个循环的时候level是-1,cur是0层最后一个节点
return cur.key;
}
/**
* 根据key在跳表中查询值
* @param key
* @return
*/
public V get(K key) {
if(key == null) return null;
//最高层maxLevel开始一直找到最底层找到0层小于key的最后一个节点
SkipListNode<K, V> less = mostRightLessNodeInTree(key);
return less.nextNodes.get(0) == null? null : less.nextNodes.get(0).isKeyEqualsTo(key)? less.nextNodes.get(0).value : null;
}
public void put(K key, V value) {
//跳表不接受空值的key
if(key == null) return;
SkipListNode<K, V> pre = mostRightLessNodeInTree(key);
SkipListNode<K, V> preNext = pre.nextNodes.get(0);
//如果元素已经存在,更新元素的值
if(preNext != null && preNext.isKeyEqualsTo(key)) {
preNext.value = value;
} else {
//如果不存在增加这个元素
//首先size++
size ++;
//新的节点的层数
int newNodeLevel = 0;
//相当于抛硬币,随机得到的值小于PROBABILITY就增加1继续抛,直到大于等于PROBABILITY
while(Math.random() < PROBABILITY) {
newNodeLevel ++;
}
SkipListNode<K, V> newNode = new SkipListNode<>(key, value);
while(maxLevel < newNodeLevel) {
maxLevel ++;
head.nextNodes.add(null);
}
for(int i = 0; i <= newNodeLevel; i++) {
newNode.nextNodes.add(null);
}
int level = maxLevel;
SkipListNode<K, V> preNode = head;
while(level >= 0) {
preNode = mostRightLessNodeInLevel(key, preNode, level);
if(level <= newNodeLevel) {
newNode.nextNodes.set(level, preNode.nextNodes.get(level));
preNode.nextNodes.set(level, newNode);
}
level --;
}
}
}
public void remove(K key) {
if(containsKey(key)) {
//删除的时候整个跳表的size需要-1
size --;
//从最高层的head节点开始找,找到每一个都删除
SkipListNode<K, V> pre = head;
int level = maxLevel;
while(level >= 0) {
//查找当前层的小于key的最右边的节点
pre = mostRightLessNodeInLevel(key, pre, level);
//next是pre在当前层的下一个节点,如果key在当前层存在,那next就应该是key所代表的元素
SkipListNode<K, V> next = pre.nextNodes.get(level);
//如果next就是key所代表的元素,那把pre的next指向next的下一个
if(pre.nextNodes.get(level) != null && pre.nextNodes.get(level).isKeyEqualsTo(key)) {
pre.nextNodes.set(level, next.nextNodes.get(level));
//如果当前节点在当前层的前一个节点是head而且当前节点后面没有其他的了,那这一层删除
if(pre == head && next.nextNodes.get(level) == null) {
head.nextNodes.remove(level);
//删了一层,maxLevel也要减1
maxLevel --;
}
}
level --;
}
}
}
// for test
public static void printAll(SkipListMap<String, String> obj) {
for (int i = obj.maxLevel; i >= 0; i--) {
System.out.print("Level " + i + " : ");
SkipListNode<String, String> cur = obj.head;
while (cur.nextNodes.get(i) != null) {
SkipListNode<String, String> next = cur.nextNodes.get(i);
System.out.print("(" + next.key + " , " + next.value + ") ");
cur = next;
}
System.out.println();
}
}
public static void main(String[] args) {
SkipListMap<String, String> test = new SkipListMap<>();
printAll(test);
System.out.println("======================");
test.put("A", "10");
/*printAll(test);
System.out.println("======================");
test.remove("A");
printAll(test);
System.out.println("======================");*/
test.put("E", "E");
test.put("B", "B");
test.put("A", "A");
test.put("F", "F");
test.put("C", "C");
test.put("D", "D");
printAll(test);
System.out.println("======================");
System.out.println(test.containsKey("B"));
System.out.println(test.containsKey("Z"));
System.out.println(test.firstKey());
System.out.println(test.lastKey());
//System.out.println(test.floorKey("D"));
//System.out.println(test.ceilingKey("D"));
System.out.println("======================");
test.remove("D");
printAll(test);
System.out.println("======================");
//System.out.println(test.floorKey("D"));
//System.out.println(test.ceilingKey("D"));
}
}
整体来说,跳表不难,但是你需要注意边界的判断以及时时刻刻想着跳表是为了实现O(logN)的时间复杂度,而不是O(N),所以类似于从head开始沿着第0层来查找的方法肯定不是跳表的主流方法。