减少预测模型的输入变量数称为降维。
较少的输入变量可以产生更简单的预测模型,该模型在对新数据进行预测时可能具有更好的性能。
也许机器学习中最流行的降维技术是主成分分析,简称PCA。这是一种来自线性代数领域的技术,可用作数据准备技术,在拟合模型之前创建数据集的投影。
在本教程中,您将了解如何在开发预测模型时使用 PCA 进行降维。
- 降维涉及减少建模数据中输入变量或列的数量。
- PCA是线性代数中的一种技术,可用于自动执行降维。
- 如何评估使用 PCA 投影作为输入并使用新的原始数据进行预测的预测模型。
教程概述
本教程分为三个部分;它们是:
- 降维和 PCA
- PCA Scikit-Learn API
- 用于降维的PCA工作示例
降维和 PCA
降维是指减少数据集的输入变量数量。
如果数据是使用行和列表示的,例如在电子表格中,则输入变量是作为输入提供给模型以预测目标变量的列。输入变量也称为要素。
我们可以将表示n 维特征空间上维度的数据列和数据行视为该空间中的点。这是对数据集的有用几何解释。
在具有 k 个数值属性的数据集中,您可以将数据可视化为 k 维空间中的点云......
在特征空间中具有大量维度可能意味着该空间的体积非常大,反过来,我们在该空间中的点(数据行)通常代表一个小且不具代表性的样本。
这可能会极大地影响机器学习算法的性能,这些算法适合具有许多输入特征的数据,通常被称为“维度的诅咒”。
因此,通常需要减少输入要素的数量。这减少了特征空间的维数,因此称为“降维”。
降维的一种流行方法是使用线性代数领域的技术。这通常称为“特征投影”,使用的算法称为“投影方法”。
投影方法旨在减少特征空间中的维度数量,同时保留数据中观察到的变量之间最重要的结构或关系。
在处理高维数据时,通过将数据投影到捕获数据“本质”的低维子空间来降低维数通常是有用的。这称为降维。
然后,可以将生成的数据集(投影)用作训练机器学习模型的输入。
从本质上讲,原始特征不再存在,新特征是从与原始数据不直接可比的可用数据构建的,例如没有列名。
将来在进行预测时提供给模型的任何新数据(例如测试数据集和新数据集)也必须使用相同的技术进行投影。
主成分分析(PCA)可能是最流行的降维技术。
最常见的降维方法称为主成分分析或 PCA。
它可以被认为是一种投影方法,其中具有 m 列(特征)的数据投影到具有m 列或更少列的子空间中,同时保留原始数据的本质。
PCA方法可以使用线性代数工具进行描述和实现,特别是矩阵分解,如特征分解或SVD。
PCA 可以定义为将数据正交投影到低维线性空间(称为主子空间)上,使得投影数据的方差最大化
现在我们已经熟悉了用于降维的PCA,让我们看看如何将这种方法与scikit-learn库一起使用。
PCA Scikit-Learn API
我们可以使用 PCA 来计算数据集的投影,并选择投影的多个维度或主成分作为模型的输入。
scikit-learn库提供了PCA类,该类可以适应数据集,并用于转换训练数据集和将来的任何其他数据集。
例如:
|
1
2
3
4
5
6
7
8
|
...
data = ...
# define transform
pca = PCA()
# prepare transform on dataset
pca.fit(data)
# apply transform to dataset
transformed = pca.transform(data)
|
PCA 的输出可用作训练模型的输入。
最好的方法是使用管道,其中第一步是 PCA 转换,下一步是将转换后的数据作为输入的学习算法。
|
1
2
3
4
|
...
# define the pipeline
steps = [('pca', PCA()), ('m', LogisticRegression())]
model = Pipeline(steps=steps)
|
如果输入变量具有不同的单位或比例,则在执行 PCA 转换之前规范化数据也是一个好主意;例如:
|
1
2
3
4
|
...
# define the pipeline
steps = [('norm', MinMaxScaler()), ('pca', PCA()), ('m', LogisticRegression())]
model = Pipeline(steps=steps)
|
现在我们已经熟悉了 API,让我们看一个示例。
用于降维的PCA工作示例
首先,我们可以使用make_classification() 函数创建一个包含 1,000 个示例和 20 个输入特征的合成二元分类问题,其中 15 个输入是有意义的。
下面列出了完整的示例。
|
1
2
3
4
5
6
|
# test classification dataset
from sklearn.datasets import make_classification
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=7)
# summarize the dataset
print(X.shape, y.shape)
|
运行该示例将创建数据集并汇总输入和输出组件的形状。
|
1
|
(1000, 20) (1000,)
|
接下来,我们可以在此数据集上使用降维,同时拟合逻辑回归模型。
我们将使用管道,其中第一步执行 PCA 转换并选择 10 个最重要的维度或组件,然后针对这些特征拟合逻辑回归模型。我们不需要对此数据集上的变量进行规范化,因为根据设计,所有变量都具有相同的比例。
将使用重复分层交叉验证对管道进行评估,每次重复 3 次,每次重复 10 次。性能表示为平均分类准确度。
下面列出了完整的示例。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
# evaluate pca with logistic regression algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.pipeline import Pipeline
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=7)
# define the pipeline
steps = [('pca', PCA(n_components=10)), ('m', LogisticRegression())]
model = Pipeline(steps=steps)
# evaluate model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
|
运行该示例将评估模型并报告分类准确性。
注意:根据算法或评估过程的随机性质或数值精度的差异,您的结果可能会有所不同。请考虑运行几次示例并比较平均结果。
在本例中,我们可以看到具有逻辑回归的 PCA 转换实现了大约 81.8% 的性能。
|
1
|
Accuracy: 0.816 (0.034)
|
我们怎么知道将 20 个维度的输入减少到 10 个是好的还是我们能做的最好的?
我们没有;10 是一个任意的选择。
更好的方法是评估具有不同输入特征数的相同变换和模型,并选择可获得最佳平均性能的特征数(降维量)。
下面的示例执行此实验,并汇总了每个配置的平均分类准确性。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
# compare pca number of components with logistic regression algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.pipeline import Pipeline
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from matplotlib import pyplot
# get the dataset
def get_dataset():
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=7)
return X, y
# get a list of models to evaluate
def get_models():
models = dict()
for i in range(1,21):
steps = [('pca', PCA(n_components=i)), ('m', LogisticRegression())]
models[str(i)] = Pipeline(steps=steps)
return models
# evaluate a given model using cross-validation
def evaluate_model(model, X, y):
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
return scores
# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
scores = evaluate_model(model, X, y)
results.append(scores)
names.append(name)
print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.xticks(rotation=45)
pyplot.show()
|
首先运行示例将报告所选每个组件或特征数的分类精度。
注意:根据算法或评估过程的随机性质或数值精度的差异,您的结果可能会有所不同。请考虑运行几次示例并比较平均结果。
随着维度数量的增加,我们看到性能提高的总体趋势。在此数据集上,结果表明在维度数与模型的分类准确性之间进行权衡。
有趣的是,除了 15 个组件之外,我们没有看到任何改进。这符合我们对问题的定义,其中只有前 15 个组件包含有关类的信息,其余五个组件是冗余的。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
>1 0.542 (0.048)
>2 0.713 (0.048)
>3 0.720 (0.053)
>4 0.723 (0.051)
>5 0.725 (0.052)
>6 0.730 (0.046)
>7 0.805 (0.036)
>8 0.800 (0.037)
>9 0.814 (0.036)
>10 0.816 (0.034)
>11 0.819 (0.035)
>12 0.819 (0.038)
>13 0.819 (0.035)
>14 0.853 (0.029)
>15 0.865 (0.027)
>16 0.865 (0.027)
>17 0.865 (0.027)
>18 0.865 (0.027)
>19 0.865 (0.027)
>20 0.865 (0.027)
|
将创建箱须图,用于分布每个配置的维度数的精度分数。
我们可以看到分类精度随着组件数量的增加而增加的趋势,限制为 15。
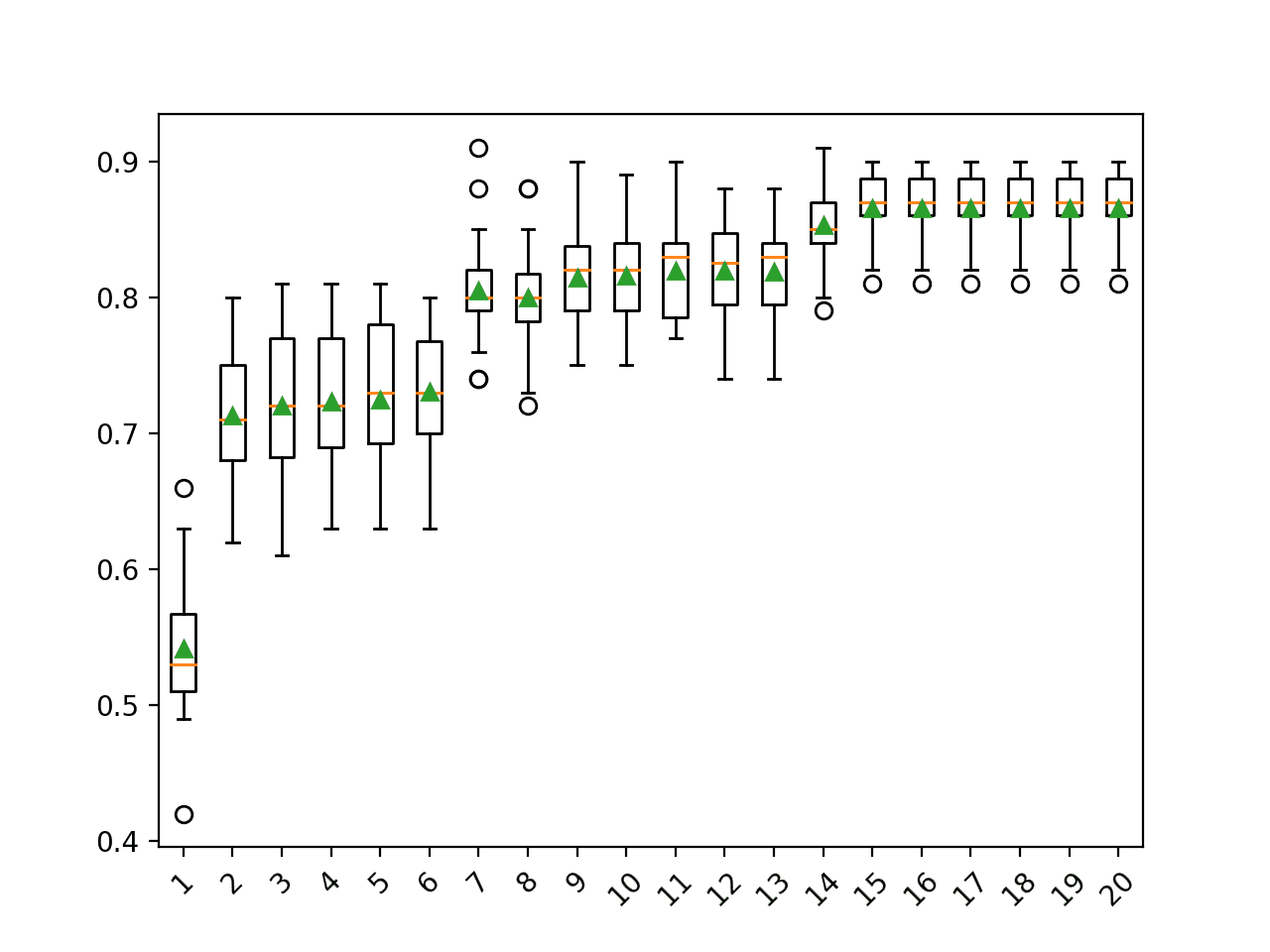
PCA 分量数与分类精度的箱形图
我们可以选择使用 PCA 变换和逻辑回归模型组合作为最终模型。
这涉及在所有可用数据上拟合管道,并使用管道对新数据进行预测。重要的是,必须对此新数据执行相同的转换,这些数据通过管道自动处理。
下面的示例提供了对新数据进行拟合和使用具有 PCA 转换的最终模型的示例。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
# make predictions using pca with logistic regression
from sklearn.datasets import make_classification
from sklearn.pipeline import Pipeline
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=7)
# define the model
steps = [('pca', PCA(n_components=15)), ('m', LogisticRegression())]
model = Pipeline(steps=steps)
# fit the model on the whole dataset
model.fit(X, y)
# make a single prediction
row = [[0.2929949,-4.21223056,-1.288332,-2.17849815,-0.64527665,2.58097719,0.28422388,-7.1827928,-1.91211104,2.73729512,0.81395695,3.96973717,-2.66939799,3.34692332,4.19791821,0.99990998,-0.30201875,-4.43170633,-2.82646737,0.44916808]]
yhat = model.predict(row)
print('Predicted Class: %d' % yhat[0])
|
运行该示例会针对所有可用数据拟合管道,并对新数据进行预测。
在这里,转换使用了 PCA 转换中最重要的 15 个组件,正如我们从上面的测试中发现的那样。
提供一行包含 20 列的新数据,并自动转换为 15 个分量并馈送到逻辑回归模型,以预测类标签。
|
1
|
Predicted Class: 1
|



![[附源码]计算机毕业设计JAVA血库管理系统](https://img-blog.csdnimg.cn/3925942d292a48c895353ca9bece4430.png)