引言
数理统计笔记的第10篇介绍了回归分析,从相关关系开始介绍,然后介绍回归分析,主要介绍了一元回归模型和多元回归模型,并对其中的原理和检验进行了叙述,最后简单介绍了一下可以化为线性回归模型的非线性回归模型。
- 引言
- 变量间的相关关系
- 相关系数的计算
- 相关系数的显著性检验
- 回归分析
- 1.一元回归模型原理
- 最小二乘法
- 回归模型
- 判定系数 r 2 r^2 r2
- 估计标准误差
- 线性关系显著性检验
- 回归系数的显著性检验
- 回归方程估计和预测
- 点估计
- 平均值点估计
- 个别值点估计
- 区间估计
- 平均值置信区间估计
- 个别值预测区间估计
- 影响区间宽度的因素
- 残差分析
- 例子
- 2.多元线性回归
- 最小二乘法
- 多重判定系数 R 2 R^2 R2
- 线性关系显著性检验
- 回归系数显著性检验
- 例子
- 3.非线性回归
- 可化为线性回归的非线性回归
- 例子
变量间的相关关系

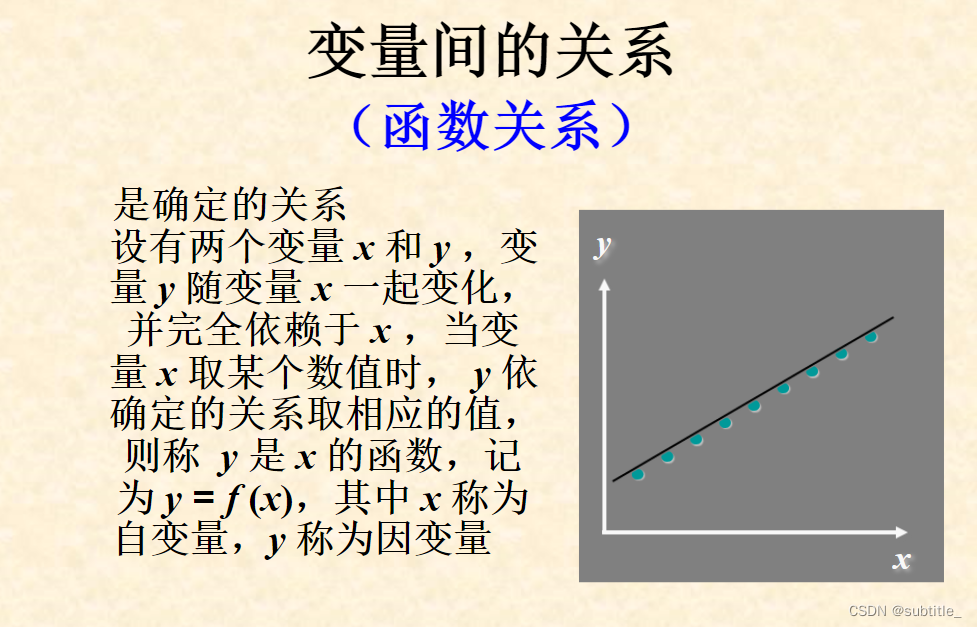
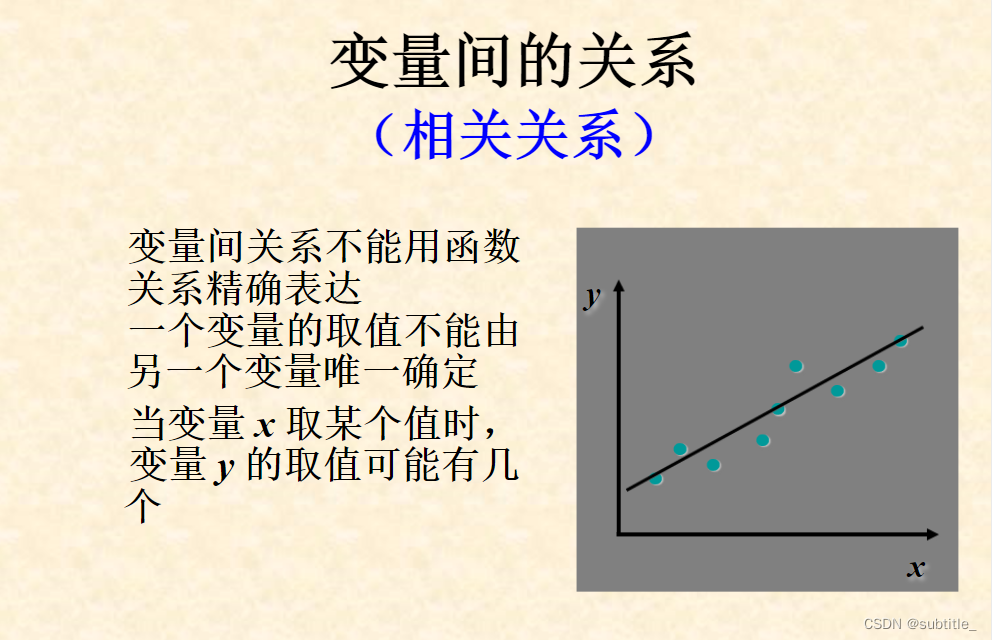
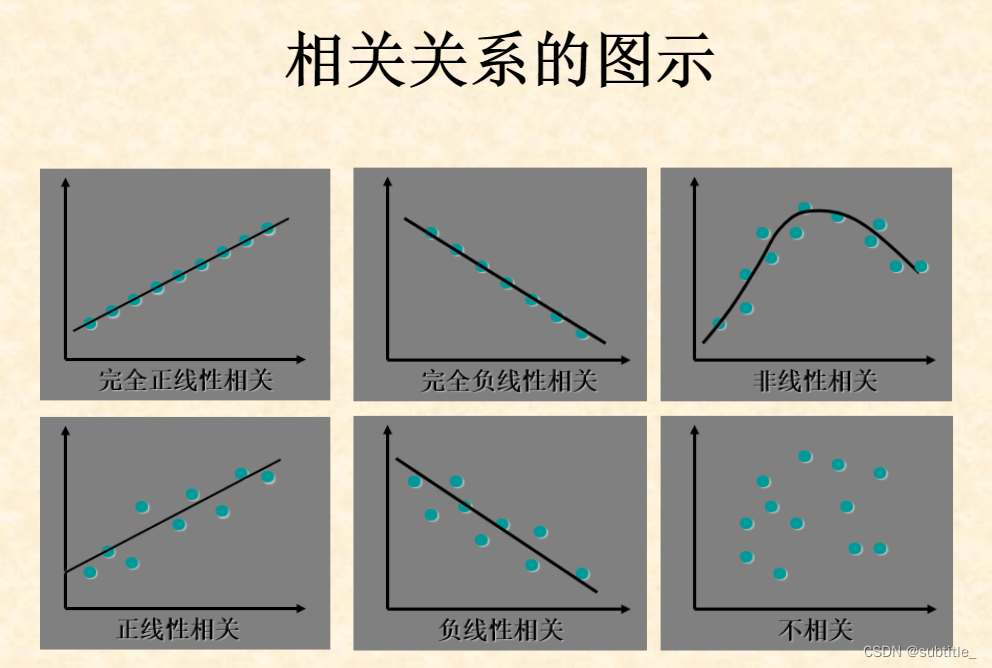
相关系数的计算



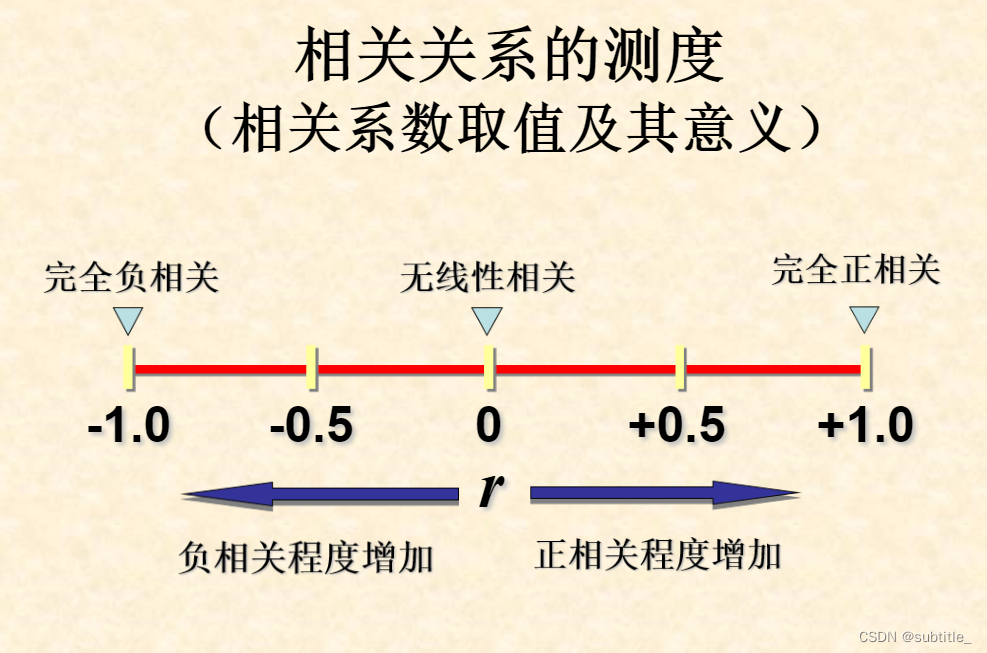
相关系数的显著性检验

回归分析


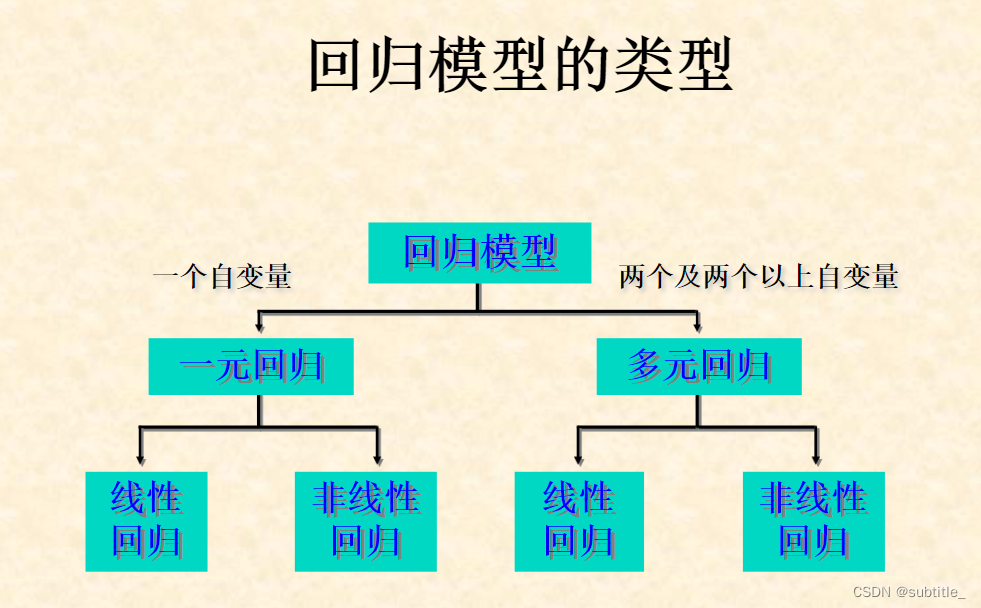

1.一元回归模型原理




最小二乘法

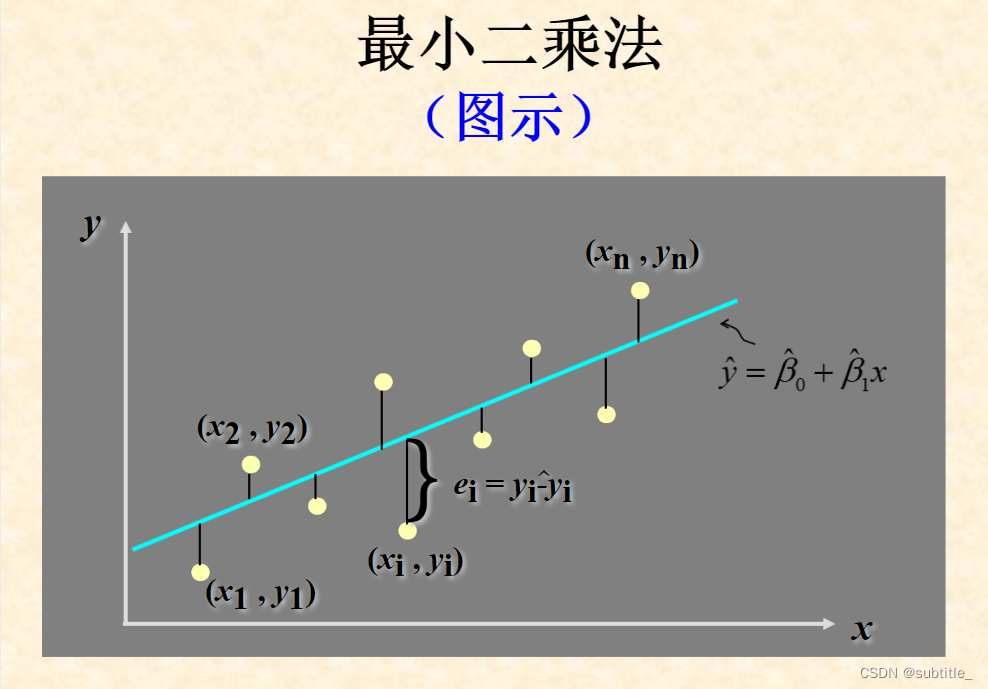

回归模型

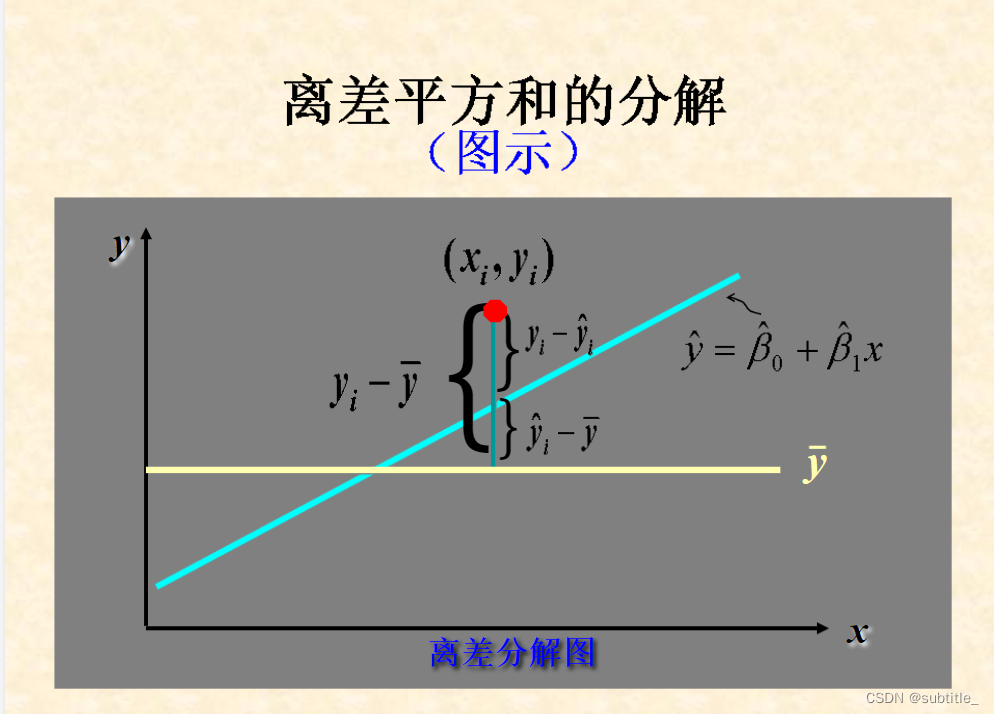

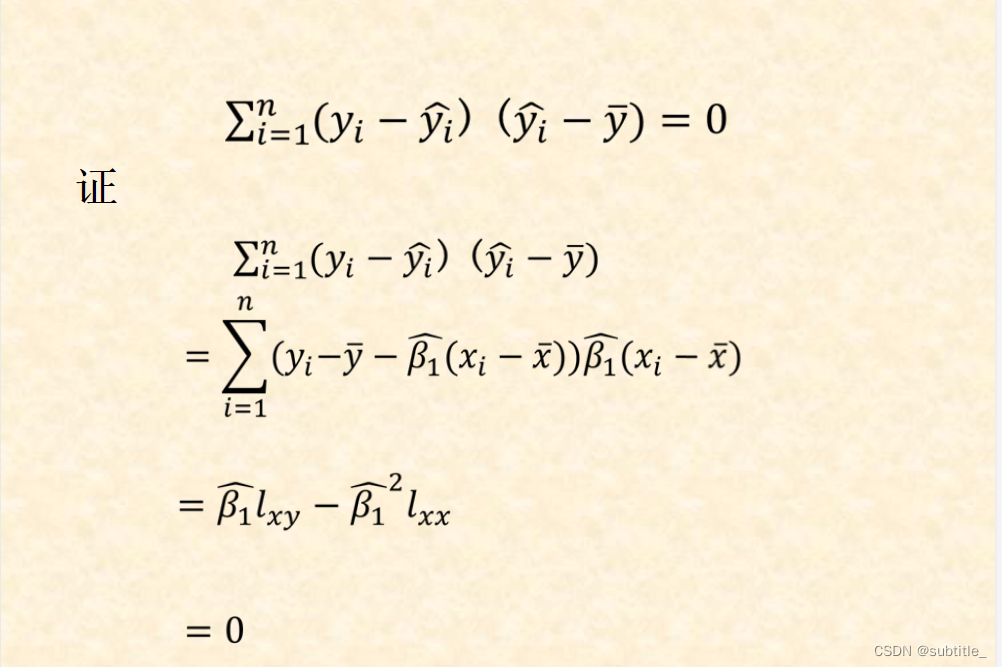
判定系数 r 2 r^2 r2
判定系数反映回归直线的拟合程度。不能说明是否具有很好的线性关系,要看是否具有线性关系需要用到下面的显著性检验的方法。

估计标准误差
实际观察值在回归直线周围的分散程度。除以
n
−
2
n-2
n−2是因为SSE的自由度是
n
−
2
n-2
n−2。

线性关系显著性检验
检验的是线性关系是否显著。使用的是F检验量。


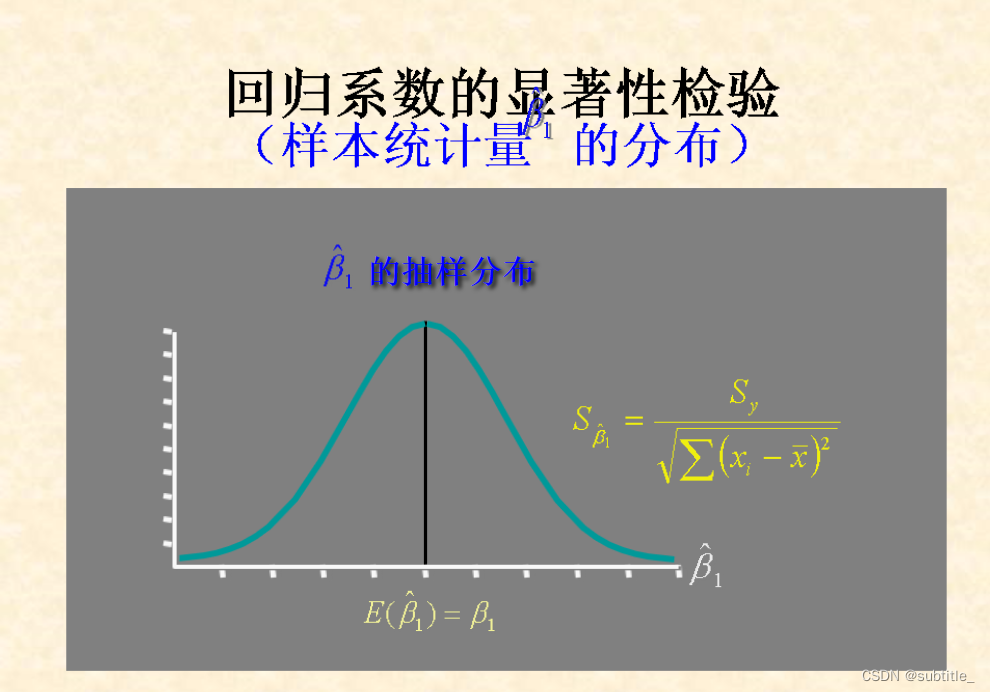
回归系数的显著性检验
检验的是是否具有线性关系。使用的是t检验量。



回归方程估计和预测

点估计

平均值点估计

个别值点估计

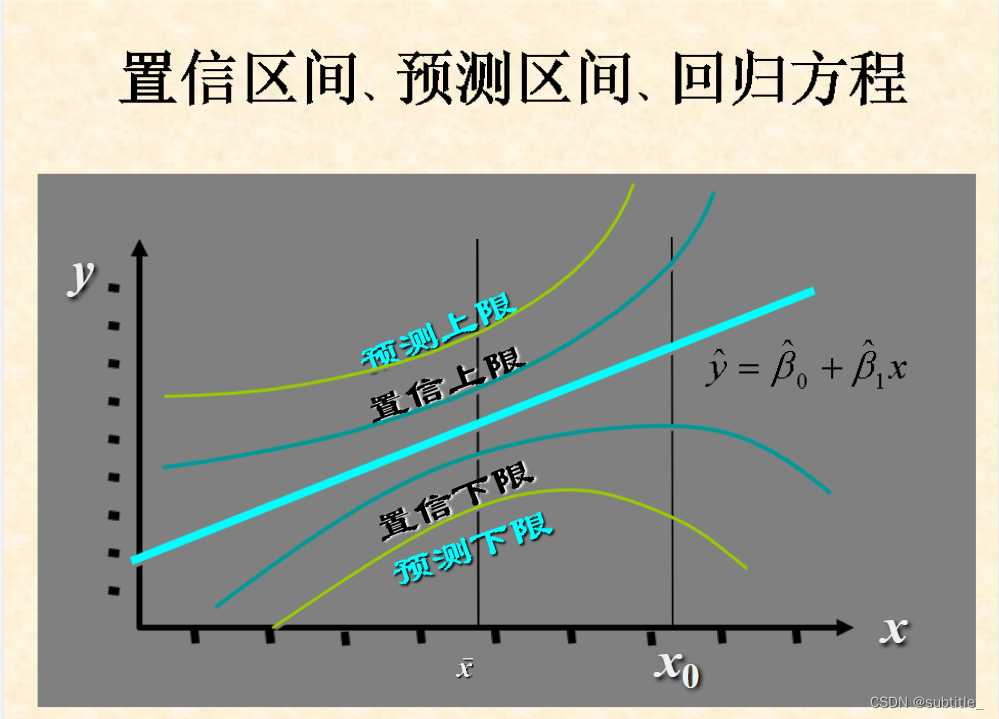
区间估计

平均值置信区间估计

个别值预测区间估计

影响区间宽度的因素

残差分析

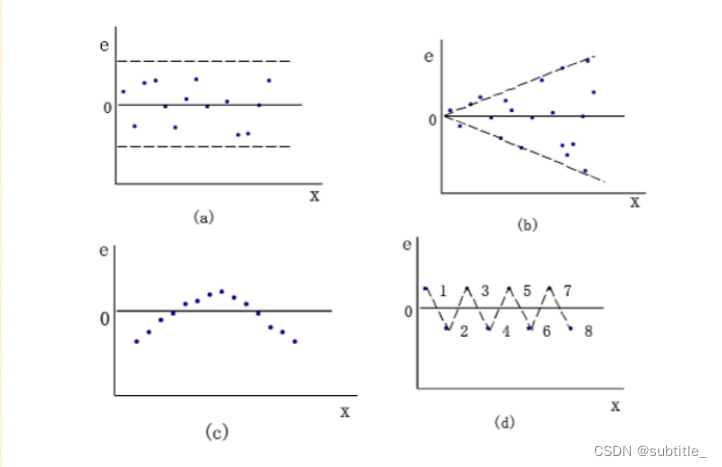

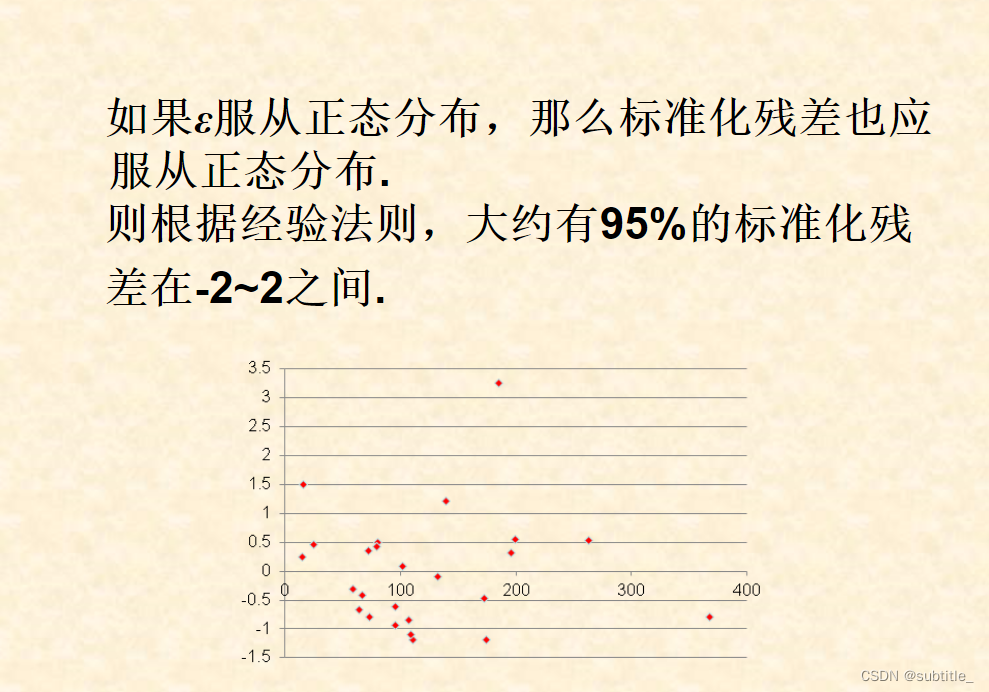
例子
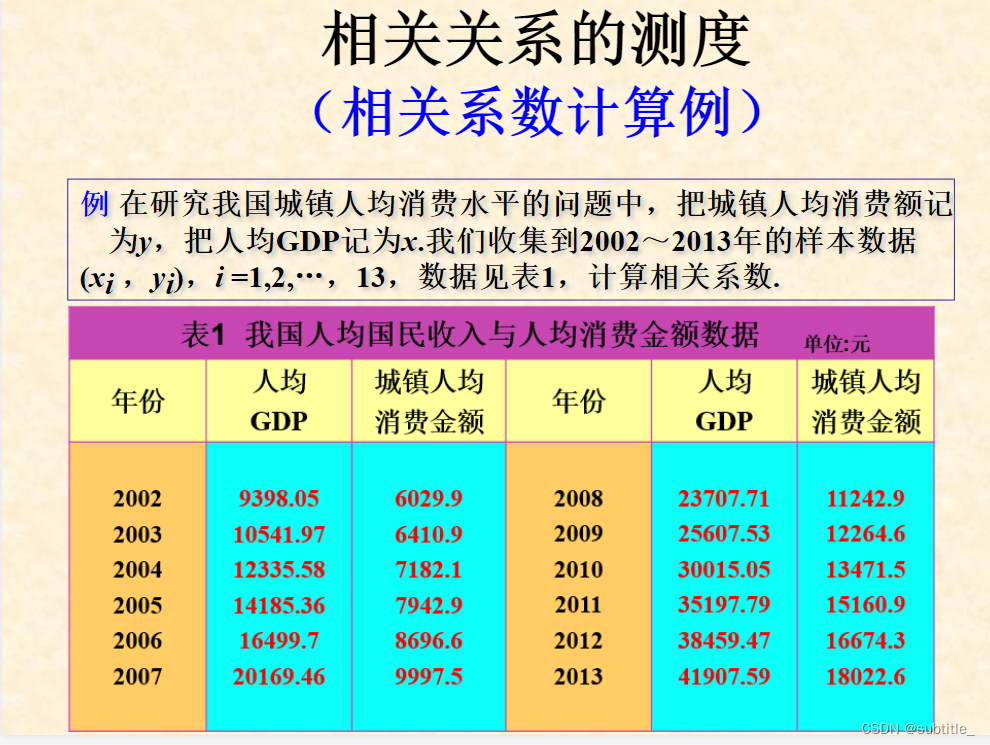

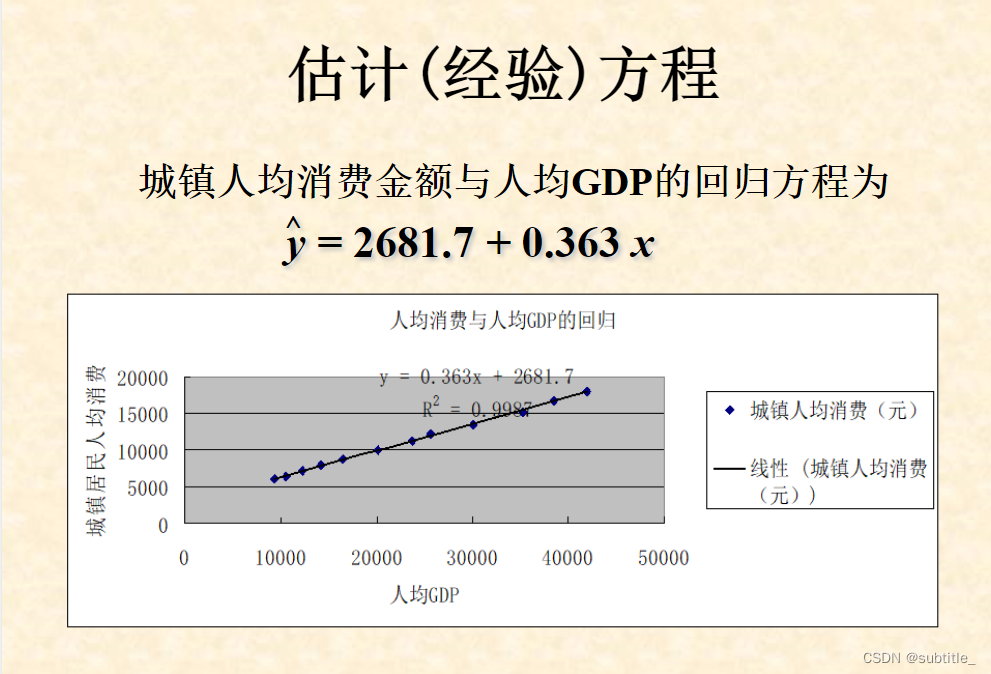


2.多元线性回归




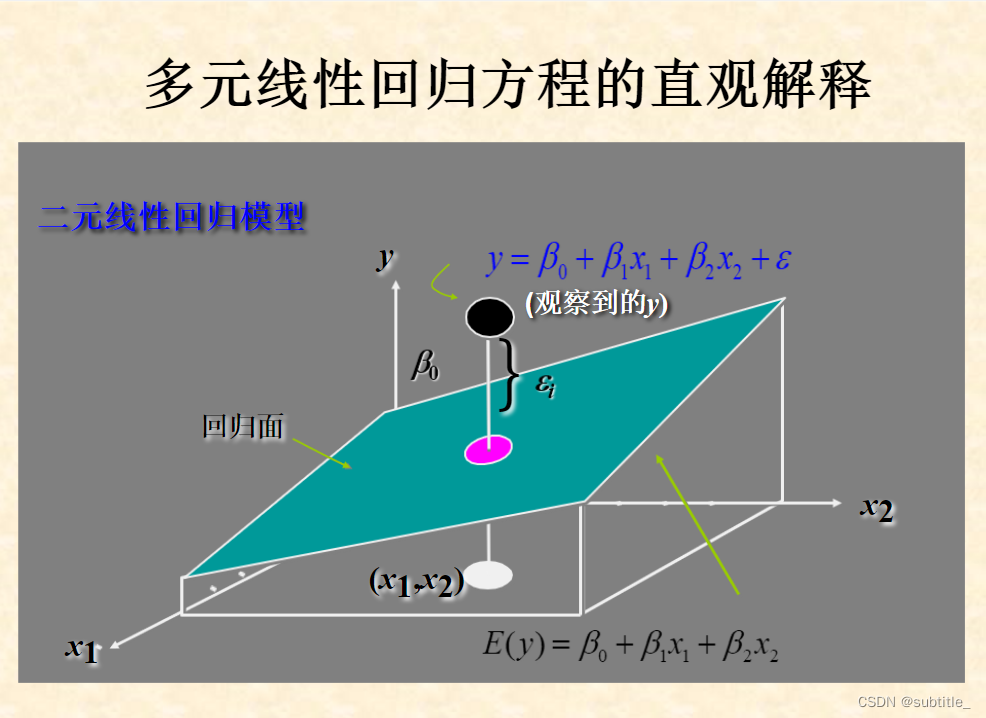

最小二乘法

多重判定系数 R 2 R^2 R2

需要进行修正。

线性关系显著性检验


回归系数显著性检验


例子
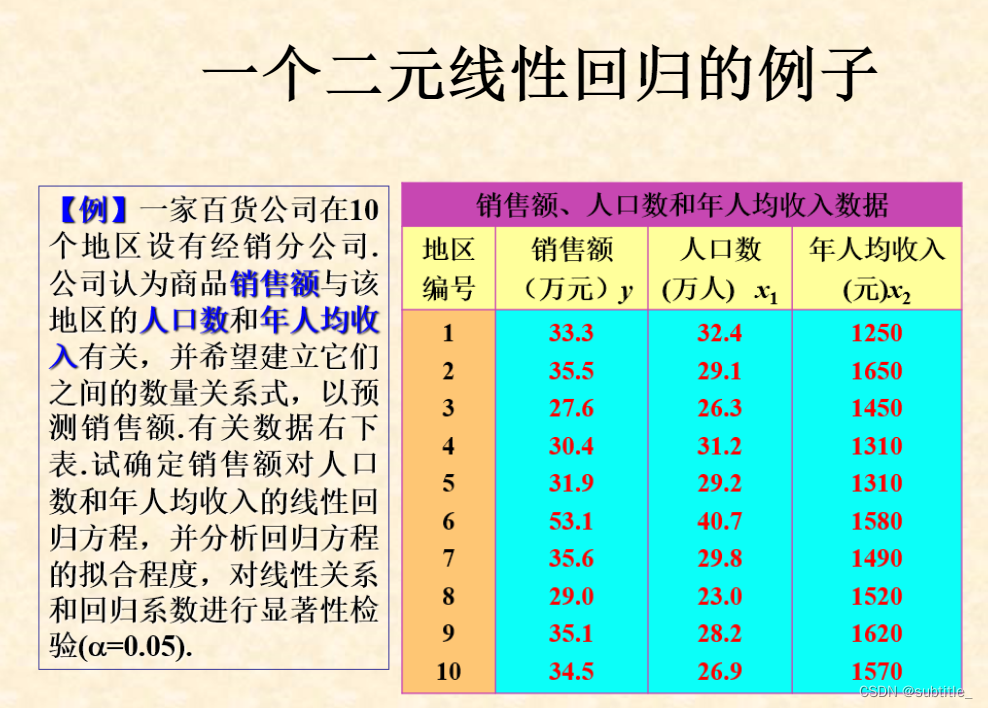


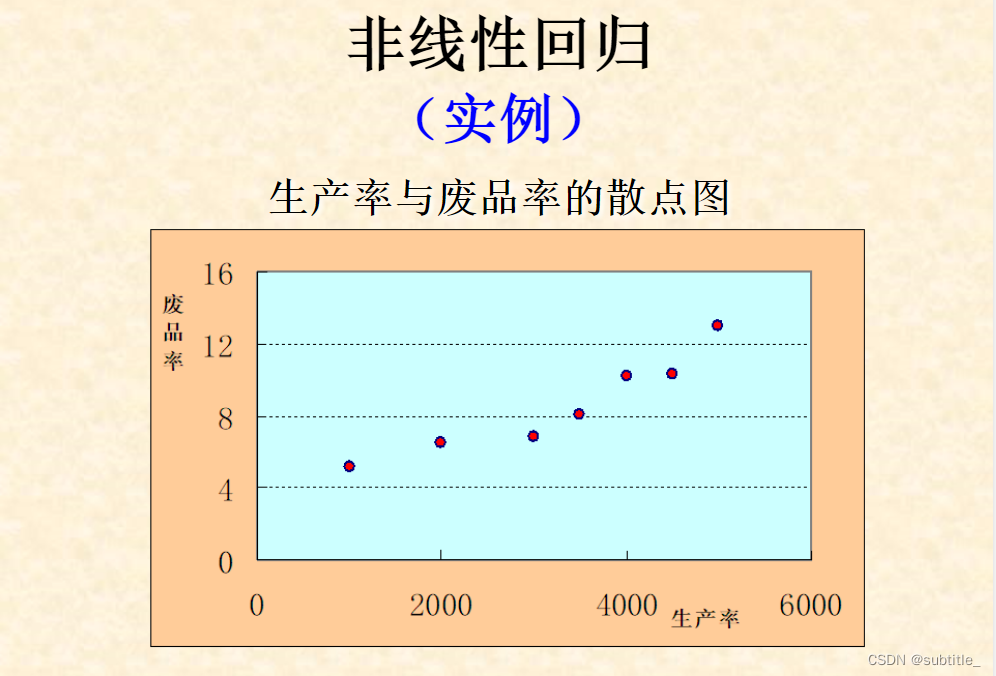
3.非线性回归
可化为线性回归的非线性回归

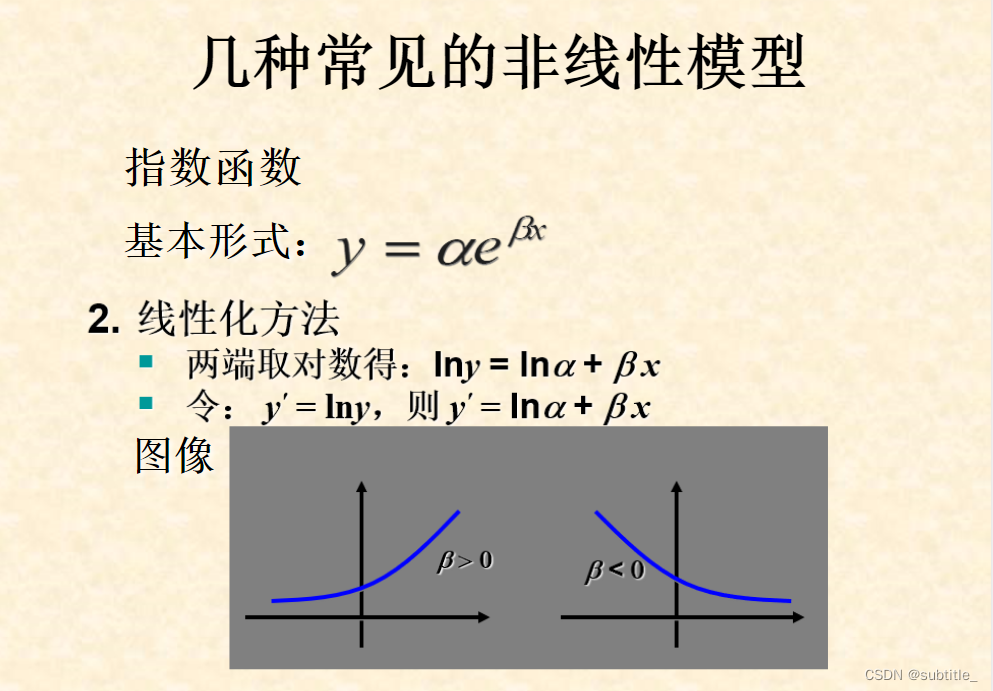
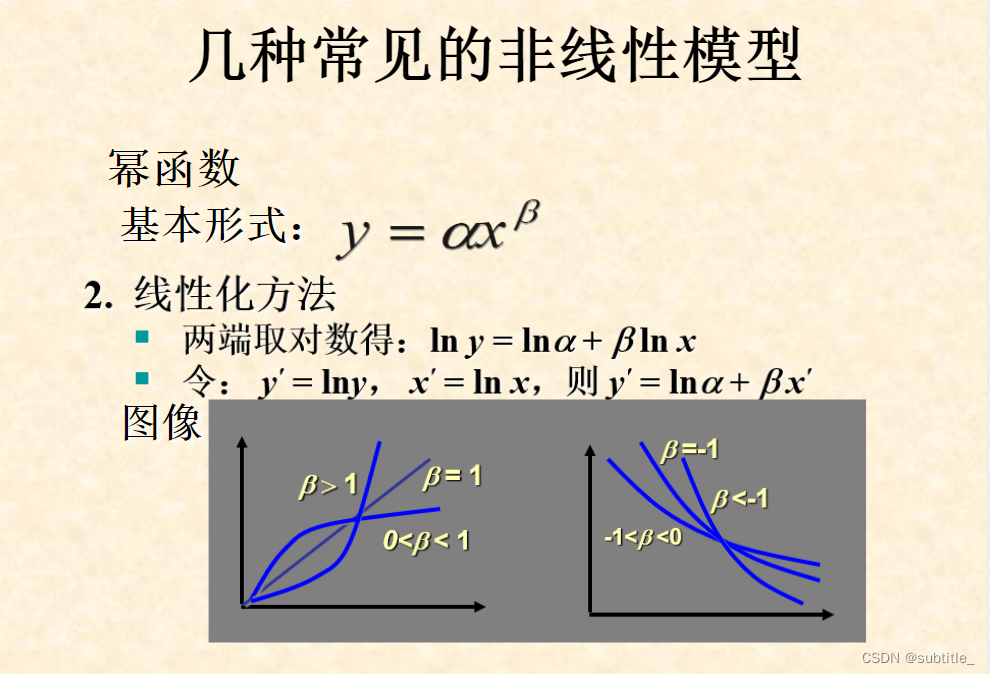
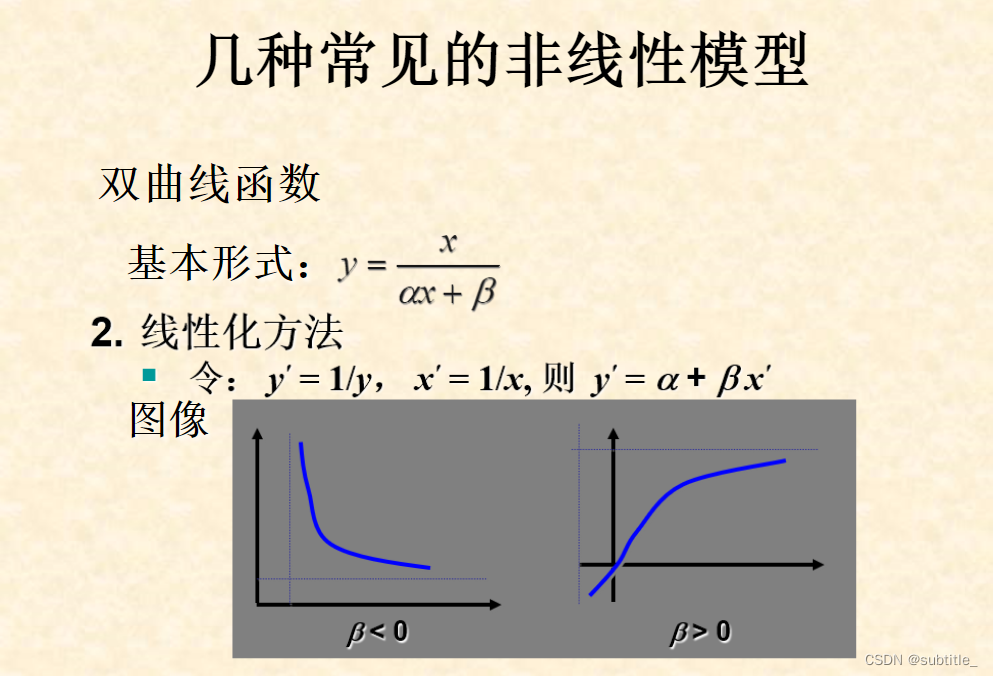
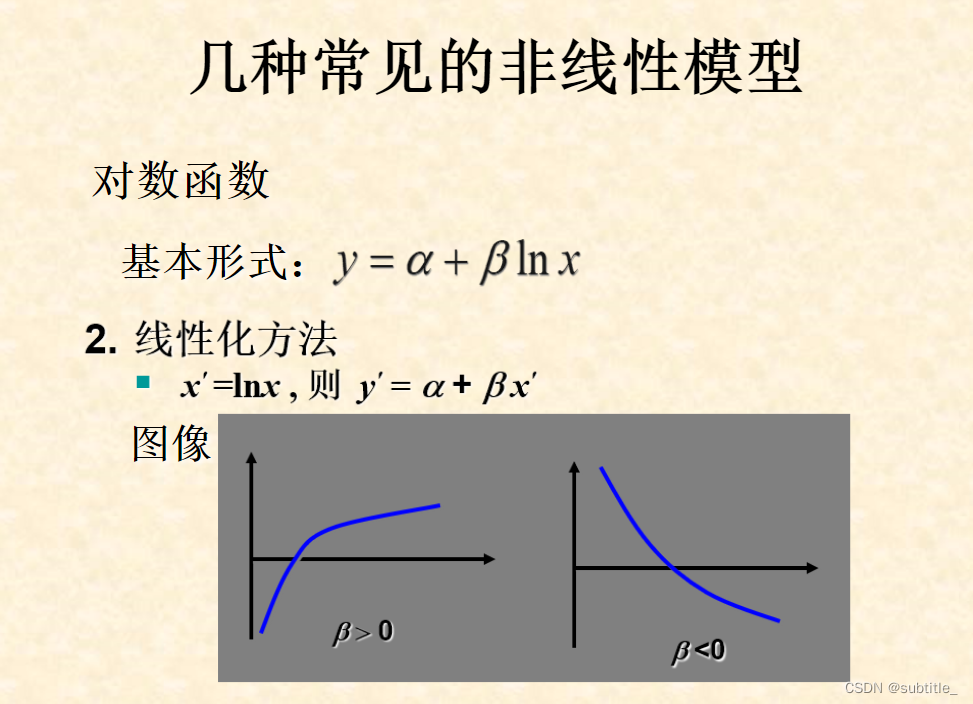
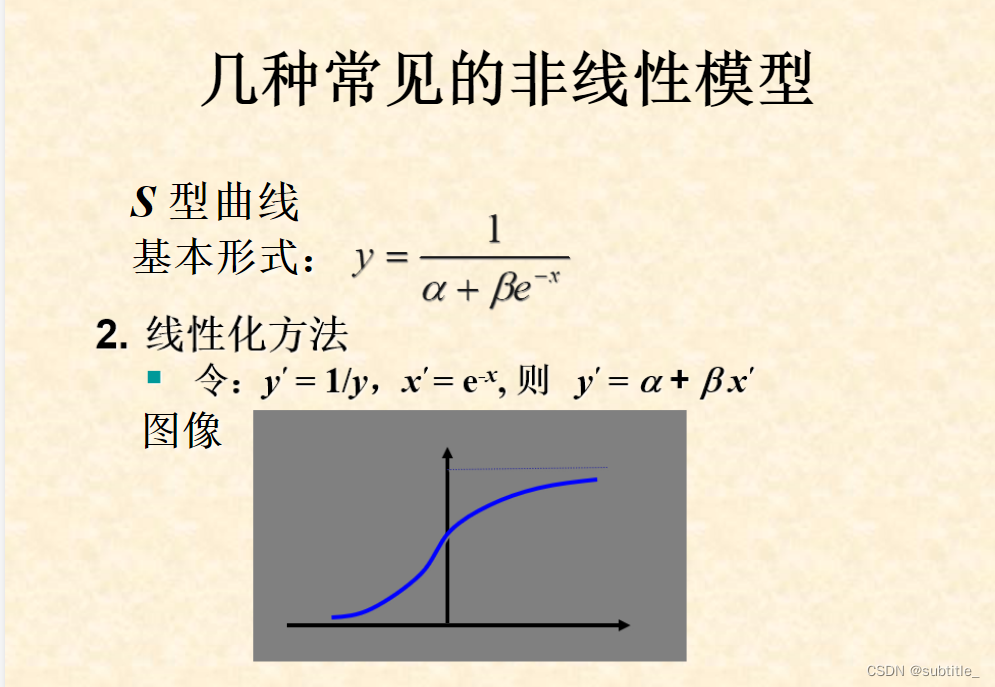
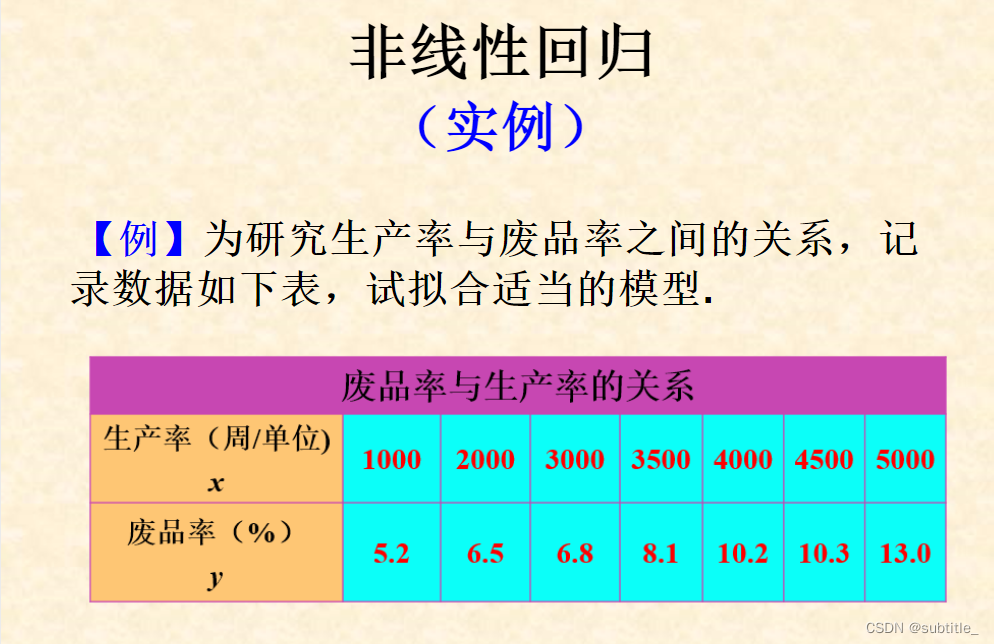
例子










![[附源码]计算机毕业设计springboot自行车租赁管理系统](https://img-blog.csdnimg.cn/80b8c104b5cc44aa92b48d2429eba31d.png)