小伙伴们好久不见，我又来了，这次我分享的内容是如何理解牛顿迭代法及如何使用牛顿迭代法求数的平方根

什么是牛顿迭代法？

官方话术：牛顿迭代法又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
简而言之，就是用来模拟近似值的一种算法。

牛顿迭代法产生背景

多数方程不存在求根公式，因此求精确根非常困难，甚至不可解，从而寻找方程的近似根就显得特别重要。

牛顿迭代法有什么用？

牛顿迭代法可以用于求解算术平方根等函数具有二阶导的场景。

牛顿迭代法的基本思想？（以求算术平方根为例）

概述：通过不断做切线求x轴交点，无限逼近

1. 构造函数 y=x^2 - n
   
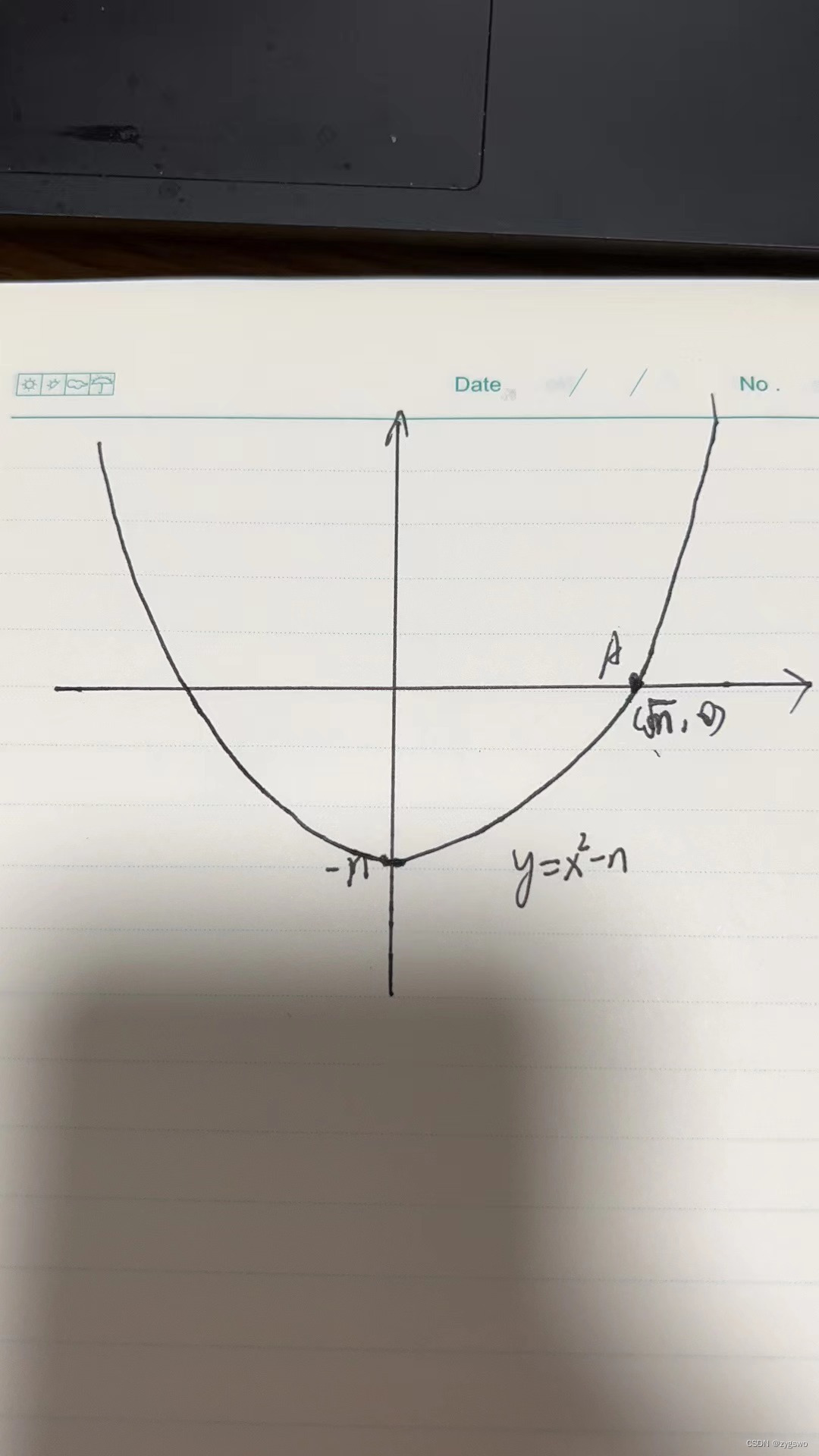
   在这里解释一下这么构造的原因，当x = 0时y的值为要求的平方数，并且该函数可以二次求导，因此可以通过牛顿迭代法求出根号n的近似值
2. 之后取靠近0的点C(1, 1-n)然后过该点作函数的切线交x轴于点B(k’, 0), 求出x=k’时函数上的点B‘(k’,k’^2 - n)
   
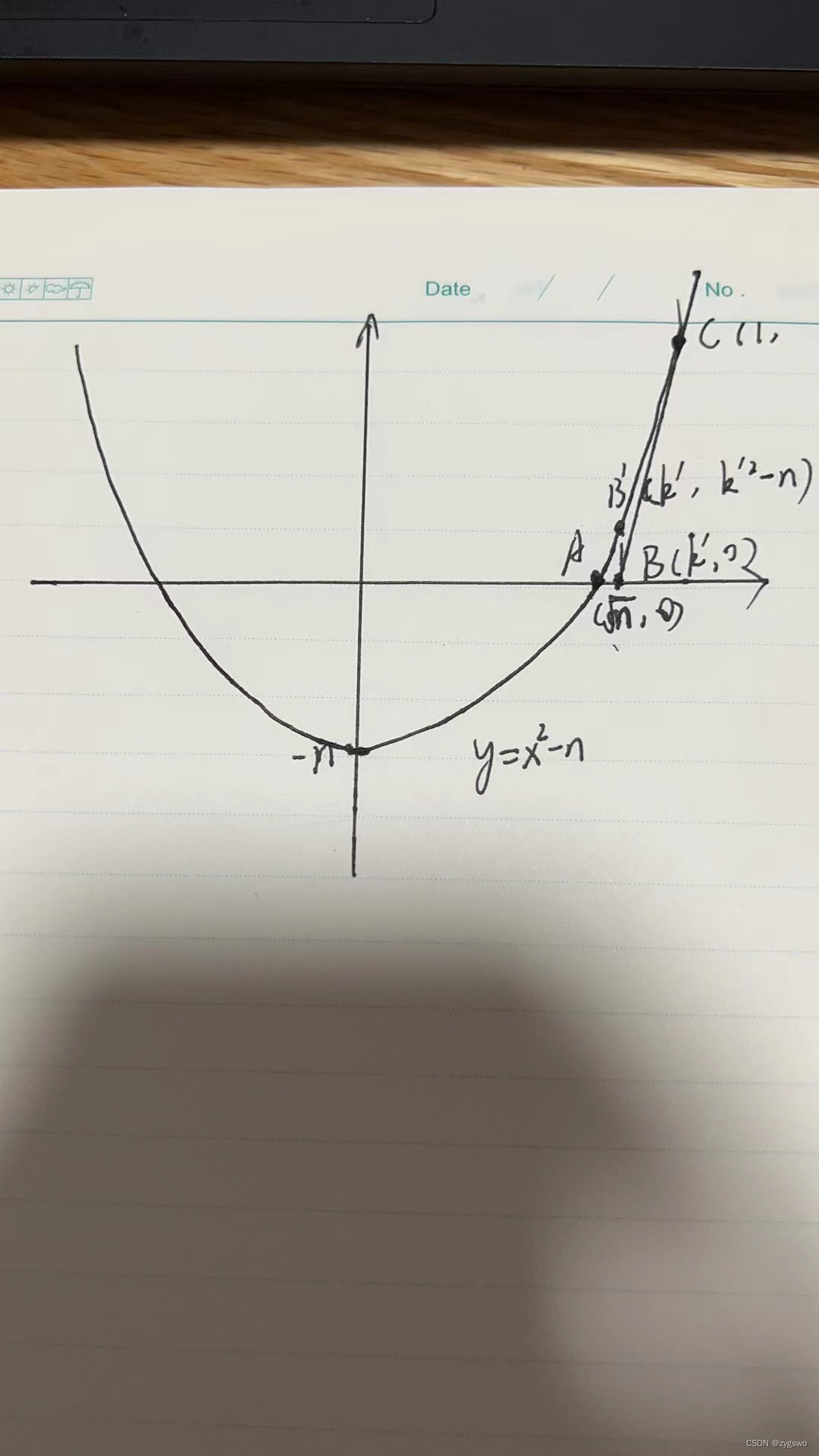
3. 之后无限迭代，经过多次迭代我们发现这个值会越来越接近A(根号n,0)
4. 取极限的值即为根号n的值

牛顿迭代法的求平方根的代码

public static double sqrt(double n) {
    double threshold= 1e-15;
    double k = 1.0;
    while (Math.abs(k*k - n) > threshold) {
        k = (k + n/k) / 2.0;
    }
    return k;
}

牛顿迭代法的求平方根的证明

1. 已知构造的函数为y = x^2 - n
2. 设C为函数上的一点，且C的横坐标值设为k，即x = k, 有 y = k^2 - n, 即C(k,k^2-n)
3. C点切线斜率设为m = (x^2 - n)’ = 2x = 2k
4. 则有切线与横坐标的交点B(k’,0), 又有m = Δy/Δx, 则有Δx = Δy/m = (k^2 - n)/ 2k,因此有k’ = k - Δx = k - (k^2 - n)/ 2k = (k^2 + n)/2k = (k + n/k) / 2，之后将x=k’ 在函数上的点作为C点重复步骤2、3、4
5. 当Δy -> 0时，即k^2 - n -> 0时，即C点无限趋近于零点时，k 即为所求的解，即根号n
6. 证毕

—————————————有任何问题欢迎在评论区留言———————————