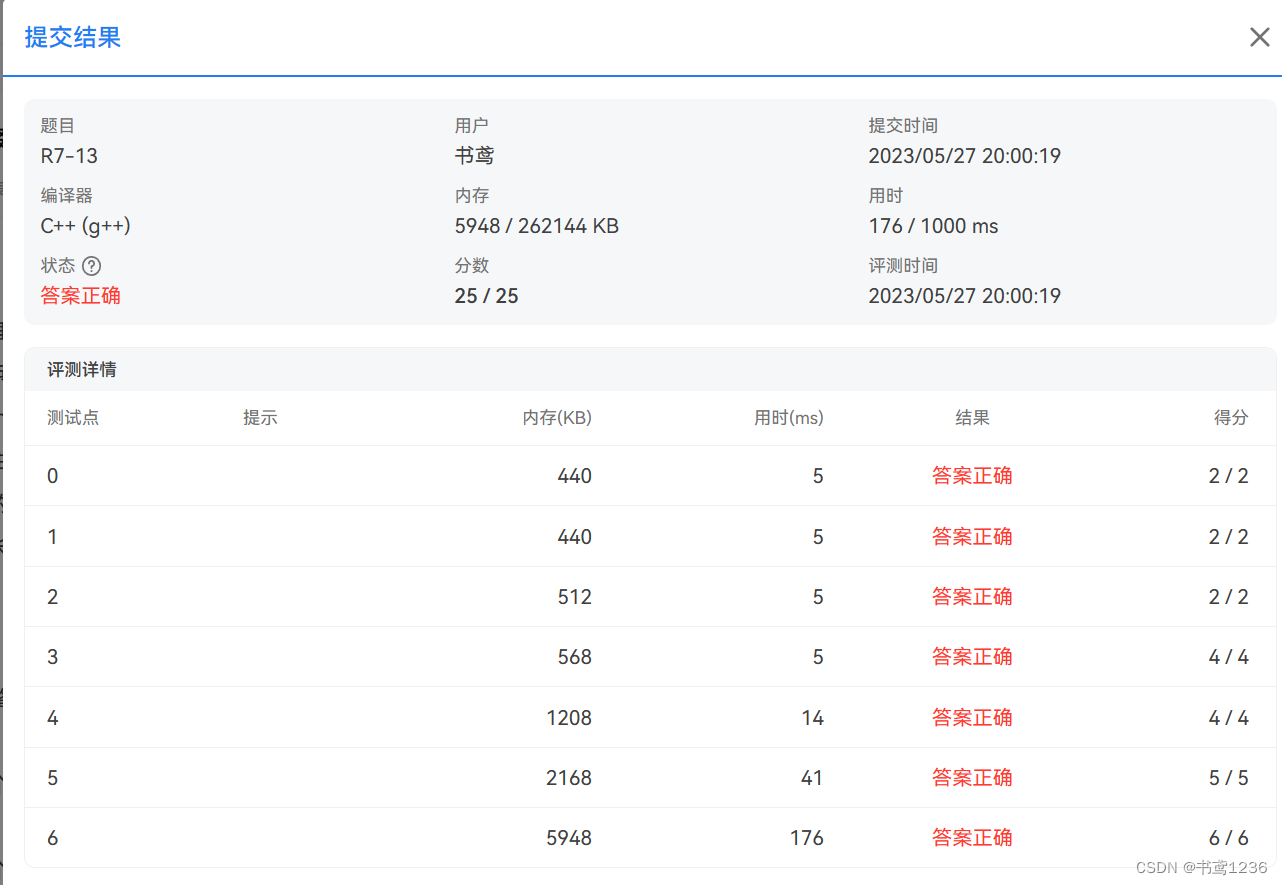
融合改进Sine混沌映射的新型粒子群优化算法(NIPSO)
文章目录
- 融合改进Sine混沌映射的新型粒子群优化算法(NIPSO)
- 1.粒子群优化算法
- 2. 改进粒子群优化算法
- 2.1 改进的 Sine 混沌映射
- 2.2 粒子群改进
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.Python代码
摘要:为了应对传统粒子群算法(PSO)存在的初始位置不均匀、易达到局部最优、搜索精度不高等问题,提出了一种基于改进Sine混沌映射的新型PSO算法。采用一种改进的Sine混沌映射技术代替传统的伪随机数方法生成初始粒子种群,以丰富种群的多样性。在原始基本位置更新公式的基础上增加两种新的位置更新机制,并分别引入一个高斯变异算子实现算法勘探性能和开发性能之间的动态平衡以及在迭代过程中使粒子有效跳出局部最优
1.粒子群优化算法
基础粒子群优化算法的具体原理参考博客
2. 改进粒子群优化算法
2.1 改进的 Sine 混沌映射
鉴于普通混沌映射都存在着不足, 往往都 是选择改进的混沌映射作为群智能优化算法的初始 化。其中改进最多两种便是 Logistic 映射和 Sine 映 射, 鉴于改进后的 Sine 混沌映射空间遍历性好, 种 群多样性丰富, 相平面内分布均匀, 同时结构简单、 效率高, 故本文选取改进 Sine 混沌映射作为改进粒 子群算法的初始化方法。改进 Sine 混沌公式如下:
{
a
i
+
1
=
sin
(
κ
π
a
i
)
b
i
+
1
=
sin
(
κ
π
b
i
)
y
i
+
1
=
(
a
i
+
1
+
b
i
+
1
)
%
1
(5)
\left\{\begin{array}{l} a_{i+1}=\sin \left(\kappa \pi a_i\right) \\ b_{i+1}=\sin \left(\kappa \pi b_i\right) \\ y_{i+1}=\left(a_{i+1}+b_{i+1}\right) \% 1 \end{array}\right.\tag{5}
⎩
⎨
⎧ai+1=sin(κπai)bi+1=sin(κπbi)yi+1=(ai+1+bi+1)%1(5)
式中:
a
i
a_i
ai 和
b
i
b_i
bi 的初始值取值范围为
(
0
,
1
)
(0,1)
(0,1); 控制参数
κ
\kappa
κ 为
1200
;
y
i
+
1
1200 ; y_{i+1}
1200;yi+1 为迭代混沌序列值;
%
\%
% 为取余数运算。
2.2 粒子群改进
为了在优化过程的不同阶段动态协调全局搜索和局部搜索, 提出了如下新的粒子位置更新方程, 以 提高找到最优解的速度和精度, 而不削弱其全局搜 索能力。
X
i
(
t
+
1
)
=
{
X
i
(
t
)
+
V
i
(
t
+
1
)
,
r
3
>
0.5
sin
(
t
π
2
t
max
)
X
i
(
t
)
+
u
(
X
g
b
(
t
)
−
X
i
(
t
)
)
,
λ
i
max
(
t
)
>
α
(
1
+
v
)
X
i
(
t
)
,
λ
i
max
(
t
)
≤
α
}
r
3
≤
0.5
sin
(
t
π
2
t
max
)
(6)
\begin{aligned} & \boldsymbol{X}_i(t+1)= \\ & \left\{\begin{array}{lr} \boldsymbol{X}_i(t)+\boldsymbol{V}_i(t+1), & r_3>0.5 \sin \left(\frac{t \pi}{2 t_{\max }}\right) \\ \boldsymbol{X}_i(t)+u\left(\boldsymbol{X}_{\mathrm{gb}}(t)-\boldsymbol{X}_i(t)\right), \lambda_{i \max }(t)>\alpha \\ (1+v) \boldsymbol{X}_i(t), & \lambda_{i \text { max }}(t) \leq \alpha \end{array}\right\} r_3 \leq 0.5 \sin \left(\frac{t \pi}{2 t_{\max }}\right) \end{aligned}\tag{6}
Xi(t+1)=⎩
⎨
⎧Xi(t)+Vi(t+1),Xi(t)+u(Xgb(t)−Xi(t)),λimax(t)>α(1+v)Xi(t),r3>0.5sin(2tmaxtπ)λi max (t)≤α⎭
⎬
⎫r3≤0.5sin(2tmaxtπ)(6)
式中:
t
max
t_{\max }
tmax 为总迭代次数;
r
3
r_3
r3 为
[
0
,
1
]
[0,1]
[0,1] 之间的随机数;
α
\alpha
α 为变异因子;
v
v
v 和
u
u
u 是服从高斯分布的随机数;
λ
i
max
(
t
)
\lambda_{i \max }(t)
λimax(t) 是所有维度中
X
i
(
t
)
\boldsymbol{X}_i(t)
Xi(t) 和
X
g
b
(
t
)
\boldsymbol{X}_{\mathrm{gb}}(t)
Xgb(t) 之间的最大差值 的权重, 可以描述为
{
λ
imax
(
t
)
=
max
{
λ
i
1
(
t
)
,
λ
i
2
(
t
)
,
…
,
λ
i
k
(
t
)
,
…
,
λ
i
n
(
t
)
}
λ
i
k
(
t
)
=
∣
x
i
k
(
t
)
−
x
g
b
k
(
t
)
∣
∣
x
g
b
k
(
t
)
∣
(7)
\left\{\begin{array}{l} \lambda_{\text {imax }}(t)=\max \left\{\lambda_{i 1}(t), \lambda_{i 2}(t), \ldots, \lambda_{i k}(t), \ldots, \lambda_{i n}(t)\right\} \\ \lambda_{i k}(t)=\frac{\left|x_{i k}(t)-x_{\mathrm{gbk}}(t)\right|}{\left|x_{\mathrm{gbk}}(t)\right|} \end{array}\right.\tag{7}
{λimax (t)=max{λi1(t),λi2(t),…,λik(t),…,λin(t)}λik(t)=∣xgbk(t)∣∣xik(t)−xgbk(t)∣(7)
式中:
x
i
k
(
t
)
x_{i k}(t)
xik(t) 是第
t
t
t 次迭代时第
i
i
i 个粒子位置的第
k
k
k 维 值,
x
g
b
k
(
t
)
x_{\mathrm{gb} k}(t)
xgbk(t) 是第
t
t
t 次迭代时全局最佳位置的第
k
k
k 维值, 而
λ
i
k
(
t
)
\lambda_{i k}(t)
λik(t) 则是
x
i
k
(
t
)
x_{i k}(t)
xik(t) 与
x
g
b
k
(
t
)
x_{\mathrm{gb} k}(t)
xgbk(t) 之间的差值与
x
g
b
k
(
t
)
x_{\mathrm{gb} k}(t)
xgbk(t) 的比值。 应注意, 随机数
u
u
u 和
v
v
v 服从式(8)中的高斯分布。
{
u
∼
N
(
1
,
σ
u
2
)
,
σ
u
=
μ
cos
(
(
t
−
1
)
π
2
t
max
)
v
∼
N
(
r
4
,
σ
v
2
)
,
σ
v
=
r
5
(8)
\left\{\begin{array}{l} u \sim \mathrm{N}\left(1, \sigma_u^2\right), \sigma_u=\sqrt{\mu \cos \left(\frac{(t-1) \pi}{2 t_{\max }}\right)} \\ v \sim \mathrm{N}\left(r_4, \sigma_v^2\right), \sigma_v=r_5 \end{array}\right.\tag{8}
⎩
⎨
⎧u∼N(1,σu2),σu=μcos(2tmax(t−1)π)v∼N(r4,σv2),σv=r5(8)
式中:
r
4
r_4
r4 为
[
−
1.5
,
1.5
]
[-1.5,1.5]
[−1.5,1.5] 之间的随机数,
r
5
r_5
r5 为
[
0
,
1
]
[0,1]
[0,1] 之间的 随机数,
μ
\mu
μ 是由式 (9) 确定的自适应系数。
式中:
r
4
r_4
r4 为
[
−
1.5
,
1.5
]
[-1.5,1.5]
[−1.5,1.5] 之间的随机数,
r
5
r_5
r5 为
[
0
,
1
]
[0,1]
[0,1] 之间的 随机数,
μ
\mu
μ 是由式 (9) 确定的自适应系数。
μ
=
{
20
3
λ
i
max
2
(
t
)
−
7
λ
i
max
(
t
)
+
7
3
,
α
<
λ
i
max
(
t
)
≤
0.5
0.3
,
λ
i
max
(
t
)
>
0.5
(9)
\mu= \begin{cases}\frac{20}{3} \lambda_{i \text { max }}^2(t)-7 \lambda_{i \text { max }}(t)+\frac{7}{3}, & \alpha<\lambda_{i \max }(t) \leq 0.5 \\ 0.3, & \lambda_{i \text { max }}(t)>0.5\end{cases} \tag{9}
μ={320λi max 2(t)−7λi max (t)+37,0.3,α<λimax(t)≤0.5λi max (t)>0.5(9)
根据式 (8) 和 (9), 可以看出, 服从高斯分布 的随机数
u
u
u 的浓度不仅受迭代次数的影响, 还受参 数
λ
max
(
t
)
\lambda_{\text {max }}(t)
λmax (t) 的影响。
考虑到惯性权重和加速度常数系数对寻找全局 最优的影响, , 加入了个体和全局 最优适应度的影响, 使惯性权重自适应调整, 而加速 度系数则直接采用了文献表达方式。因此, 惯 性系数
w
i
w_i
wi 和加速度系数
c
1
、
c
2
c_1 、 c_2
c1、c2 可以分别表示为:
w
i
=
{
∣
w
max
f
(
X
g
b
(
t
)
)
f
(
X
p
b
i
(
t
)
)
−
(
w
max
−
w
min
)
t
t
max
∣
,
f
(
X
p
b
i
(
t
)
)
>
0
w
max
−
(
w
max
−
w
min
)
t
t
max
,
f
(
X
p
b
i
(
t
)
)
=
0
∣
w
max
f
(
X
p
b
i
(
t
)
)
f
(
X
g
b
(
t
)
)
−
(
w
max
−
w
min
)
t
t
max
∣
,
f
(
X
p
b
i
(
t
)
)
<
0
(10)
w_i=\left\{\begin{array}{cc} \left|\frac{w_{\max } f\left(\boldsymbol{X}_{\mathrm{gb}}(t)\right)}{f\left(\boldsymbol{X}_{\mathrm{pbi}}(t)\right)}-\frac{\left(w_{\max }-w_{\min }\right) t}{t_{\max }}\right|, & f\left(\boldsymbol{X}_{\mathrm{pbi}}(t)\right)>0 \\ w_{\max }-\frac{\left(w_{\max }-w_{\min }\right) t}{t_{\max }}, & f\left(\boldsymbol{X}_{\mathrm{pbi}}(t)\right)=0 \\ \left|\frac{w_{\max } f\left(\boldsymbol{X}_{\mathrm{pbi}}(t)\right)}{f\left(\boldsymbol{X}_{\mathrm{gb}}(t)\right)}-\frac{\left(w_{\max }-w_{\min }\right) t}{t_{\max }}\right|, & f\left(\boldsymbol{X}_{\mathrm{pbi}}(t)\right)<0 \end{array}\right.\tag{10}
wi=⎩
⎨
⎧
f(Xpbi(t))wmaxf(Xgb(t))−tmax(wmax−wmin)t
,wmax−tmax(wmax−wmin)t,
f(Xgb(t))wmaxf(Xpbi(t))−tmax(wmax−wmin)t
,f(Xpbi(t))>0f(Xpbi(t))=0f(Xpbi(t))<0(10)
{
c
1
=
2.5
−
2
t
t
max
c
2
=
0.5
+
2
t
t
max
(11)
\left\{\begin{array}{l} c_1=2.5-\frac{2 t}{t_{\max }} \\ c_2=0.5+\frac{2 t}{t_{\max }} \end{array}\right.\tag{11}
{c1=2.5−tmax2tc2=0.5+tmax2t(11)
式中:
w
min
w_{\text {min }}
wmin 为惯性权重的最小值,
w
max
w_{\max }
wmax 为惯性权重的 最大值,
f
p
b
i
f_{\mathrm{pb} i}
fpbi 为粒子的个体最优适应性,
f
g
b
f_{\mathrm{gb}}
fgb 为粒子的 全局最优适应性。
3.实验结果

4.参考文献
[1]刘磊,姜博文,周恒扬等.融合改进Sine混沌映射的新型粒子群优化算法[J/OL].西安交通大学学报:1-11[2023-05-25].http://kns.cnki.net/kcms/detail/61.1069.T.20230512.1619.002.