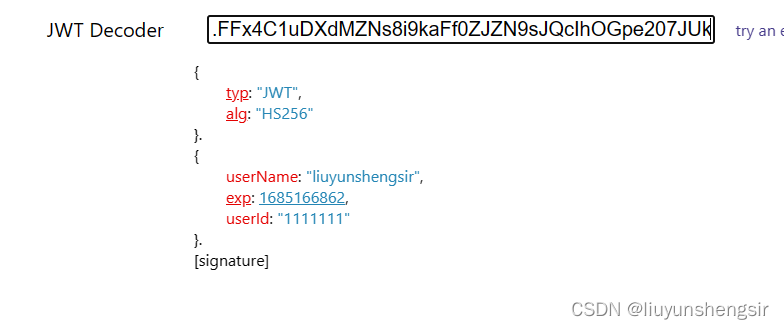
准备入门一下机器学习算法。
今天学习了线性回归，都是理论的东西，没有对于代码的实现，代码也会跟着进度好好搞一下。
对于线性回归的基础概念，我感觉很依靠概率论和线性代数两门课，作为刚准备完数学一考研的我，对内容还是有点熟悉的。

1、拟合平面方程

假如一个事件Y，其受两个变量影响，设两个变量为X1,X2。
通常想要描述变量与结果之间的关系，一般是给两个变量加一个权重
但是生活中很多事件都是受变量影响而呈现出非线性增长，因此用一个确定方程来描述事件十分困难。
例如，在一个三维坐标系中得到一个数据分布空间，手绘图如图

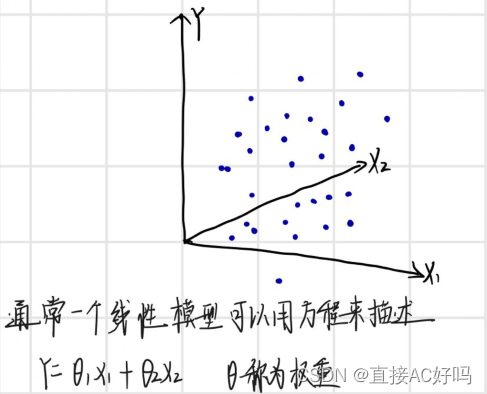
很显然，这是一种非线性分布，不能用一个确定方程来描述Y与X1，X2的关系。
但是对于这一个坐标系我们可以找出一个平面，使得让这些数据距离这个平面的整体来看是比较吻合的。也就是用一个平面来近似描述这些数据的分布。如图

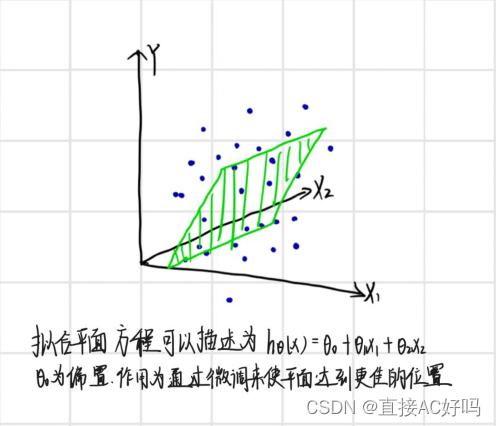
图中绿色的平面即为通过数据的整体分布而拟合出来的平面，
对于每一个数据点投影到平面上，都有一个投影点如图
对于其中的一个数据P，其实际值为P，而我们拟合在平面上的值Q即为我们的预测值。值得注意的是，两点的X1，X2都是相同的，两个点在Y上存在一个误差。

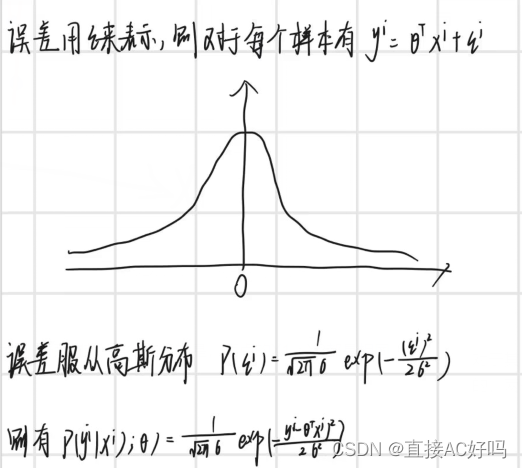
记录到这吧，公式实在打不出来，梯度下降就不更了。csdn只更新代码吧【哭】