K-means是一种经典的无监督学习算法，用于对数据进行聚类。K-means算法将数据集视为具有n个特征的n维空间，并尝试通过最小化簇内平方误差的总和来将数据点划分为簇。本文将介绍K-means算法的原理、实现和应用。

定义

• K-means是一种无监督学习算法，
• 用于对数据进行聚类。该算法将数据集分为K个簇，每个簇包含最接近其质心的数据点。K-means算法将数据集视为具有n个特征的n维空间，并尝试通过最小化簇内平方误差的总和来将数据点划分为簇。
• 它是一种迭代算法，通过将每个数据点分配到最近的质心并计算新的质心来迭代地改进簇的质量，直到质心不再变化或达到最大迭代次数为止。

实现流程（k-means算法原理）

K-means算法是一种迭代算法，其基本思想是通过将每个数据点分配到最近的质心，并计算新的质心来迭代地改进簇的质量，直到质心不再变化或达到最大迭代次数为止。具体步骤如下：

1. 随机选择K个点作为初始质心；
2. 计算每个数据点与K个质心的距离；
3. 将数据点划分到距离最近的质心所在的簇；
4. 对于每个簇，重新计算该簇内所有数据点的均值，将该均值作为新的质心；
5. 如果质心没有变化，则停止迭代。

K-means算法的核心是将数据点分配到最近的质心所在的簇，这是通过计算每个数据点与K个质心的距离来实现的。一般而言，距离可以使用欧氏距离、曼哈顿距离等来计算。而每个簇的质心则是该簇内所有数据点的均值，用于表示该簇的中心位置。

K值的选择

在K-means算法中，簇的数量k是需要事先指定的。选择合适的簇的数量非常重要。

1. 手肘法：在不同的k值下运行K-means算法，计算每个簇的误差平方和（SSE），并将其绘制成折线图。通常会发现，随着k值的增加，SSE会逐渐减小。但是，当k值增加到某个值时，SSE的下降速度会变得更加缓慢，形成一个类似手肘的拐点。该拐点所对应的k值就是比较合适的簇的数量。
2. 轮廓系数法：轮廓系数是一种用于评估聚类结果质量的指标，其取值范围在[-1, 1]之间。对于每个数据点，轮廓系数是其与同簇其他数据点距离的平均值和与最近的不同簇的所有数据点的距离的平均值之差除以两者中的较大值。聚类结果的整体轮廓系数是所有数据点的轮廓系数的平均值。较高的轮廓系数表示聚类效果较好。可以在不同的k值下运行K-means算法，计算聚类结果的整体轮廓系数，选择轮廓系数最大的k值。
3. 经验法则：在实际应用中，可以根据数据的特点、应用场景等因素，采用经验法则来选择k值。例如，对于图像分割等应用，通常选择k值为2，对于客户分类等应用，通常选择k值为3或4。

需要注意的是，K-means算法可能陷入局部最优解，因此，选择k值需要多次运行算法，比较不同的聚类结果。

创建数据

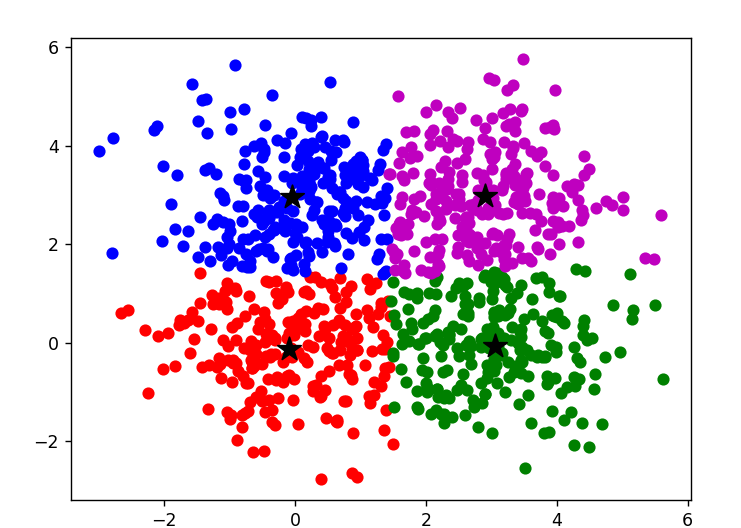
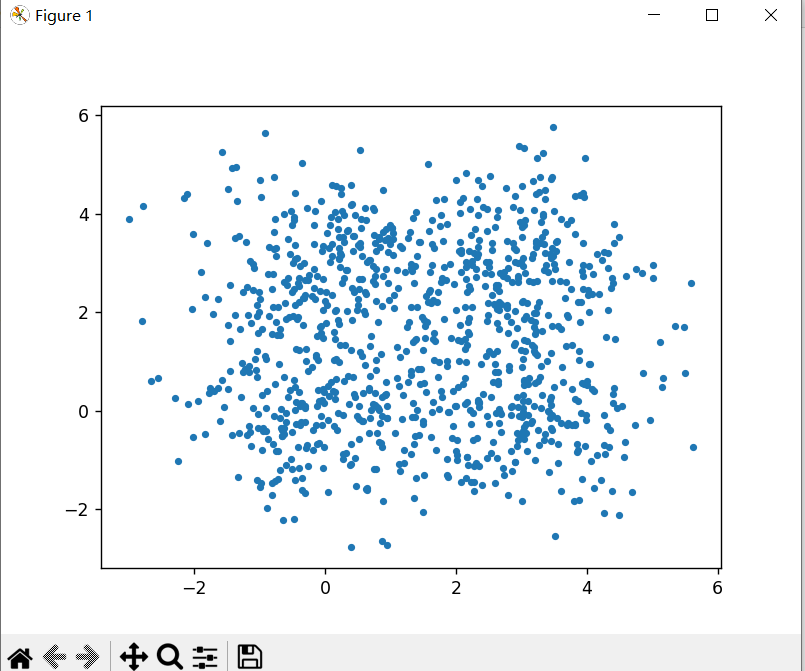
• 该代码生成了一个包含1000个数据点的随机数据集，其中有4个簇，每个簇的中心点分别位于(0,0)、(3,3)、(0,3)和(3,0)。每个簇的数据点服从正态分布。最后，用散点图可视化了数据集。可以根据需要调整数据集的大小、簇的数量、中心点的位置等参数。

	import numpy as np
	import matplotlib.pyplot as plt
	# 创建数据集
	np.random.seed(0)
	n_samples = 1000
	centers = np.array([[0, 0], [3, 3], [0, 3], [3, 0]])
	X = np.zeros((n_samples, 2))
	for i in range(len(centers)):
	X[i * (n_samples // len(centers)): (i + 1) * (n_samples // len(centers)), :] = \
	centers[i] + np.random.randn(n_samples // len(centers), 2)
	# 可视化数据集
	plt.scatter(X[:, 0], X[:, 1], s=10)
	plt.show()

实现k-means

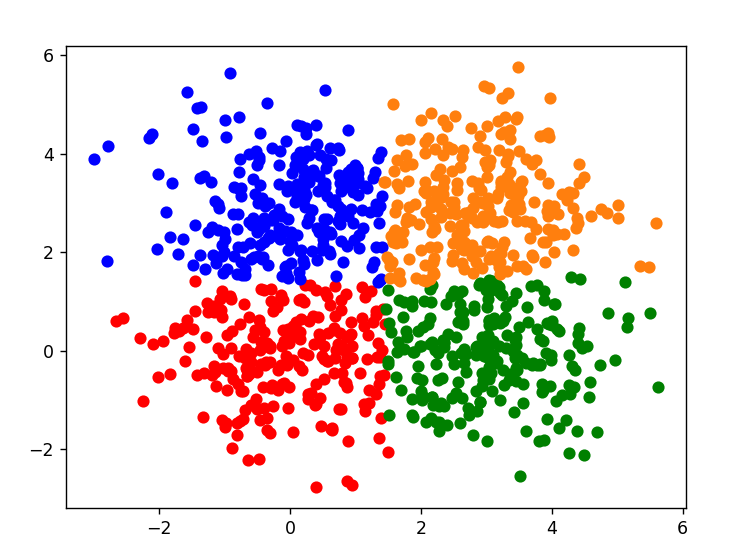
• 该代码接受一个数据矩阵X、簇的数量k和最大迭代次数max_iter作为输入，返回每个数据点的簇标签和最终的质心坐标。在每次迭代中，先计算每个数据点与k个质心的距离，然后将数据点划分到距离最近的质心所在的簇。接着，对于每个簇，重新计算该簇内所有数据点的均值，将该均值作为新的质心。最后，如果质心没有变化，则停止迭代。

	import numpy as np
	def k_means(X, k, max_iter=100):
	# 随机选择k个点作为初始质心
	centroids = X[np.random.choice(len(X), k, replace=False)]
	for i in range(max_iter):
	# 计算每个数据点与k个质心的距离
	distances = np.linalg.norm(X[:, np.newaxis, :] - centroids, axis=-1)
	# 将数据点划分到距离最近的质心所在的簇
	labels = np.argmin(distances, axis=1)
	# 对于每个簇，重新计算该簇内所有数据点的均值，将该均值作为新的质心
	new_centroids = np.array([X[labels == j].mean(axis=0) for j in range(k)])
	# 如果质心没有变化，则停止迭代
	if np.allclose(new_centroids, centroids):
	break
	centroids = new_centroids
	return labels, centroids
	if __name__ == '__main__':
	labels, centroids = k_means(X=X, k=4)
	plt.scatter(X[labels==0, 0], X[labels==0, 1], color='r')
	plt.scatter(X[labels==1, 0], X[labels==1, 1], color='g')
	plt.scatter(X[labels==2, 0], X[labels==2, 1], color='b')
	plt.scatter(X[labels==3, 0], X[labels==3, 1])
	plt.show()

优化后代码

• 在此优化后的代码中，我们使用了两个新函数
• plot_data函数用于绘制划分后的数据集
• plot_centers函数用于绘制中心点
• 在主函数中，我们先调用k_means函数得到簇标签和中心点，然后调用plot_data函数绘制划分后的数据集，最后调用plot_centers函数绘制中心点。这样的代码结构使得代码更易读，更易于调试和维护。

	import numpy as np
	import matplotlib.pyplot as plt
	# 创建数据集
	np.random.seed(0)
	n_samples = 1000
	centers = np.array([[0, 0], [3, 3], [0, 3], [3, 0]])
	X = np.zeros((n_samples, 2))
	for i in range(len(centers)):
	X[i * (n_samples // len(centers)): (i + 1) * (n_samples // len(centers)), :] = \
	centers[i] + np.random.randn(n_samples // len(centers), 2)
	# 可视化数据集
	def plot_data(X, labels):
	plt.scatter(X[labels==0, 0], X[labels==0, 1], color='r')
	plt.scatter(X[labels==1, 0], X[labels==1, 1], color='g')
	plt.scatter(X[labels==2, 0], X[labels==2, 1], color='b')
	plt.scatter(X[labels==3, 0], X[labels==3, 1], color='m')
	plt.show()
	def plot_centers(centroids):
	plt.scatter(centroids[:, 0], centroids[:, 1], s=200, marker='*', color='k')
	plt.show()
	def k_means(X, k, max_iter=100):
	# 随机选择k个点作为初始质心
	centroids = X[np.random.choice(len(X), k, replace=False)]
	for i in range(max_iter):
	# 计算每个数据点与k个质心的距离
	distances = np.linalg.norm(X[:, np.newaxis, :] - centroids, axis=-1)
	# 将数据点划分到距离最近的质心所在的簇
	labels = np.argmin(distances, axis=1)
	# 对于每个簇，重新计算该簇内所有数据点的均值，将该均值作为新的质心
	new_centroids = np.array([X[labels == j].mean(axis=0) for j in range(k)])
	# 如果质心没有变化，则停止迭代
	if np.allclose(new_centroids, centroids):
	break
	centroids = new_centroids
	return labels, centroids
	if __name__ == '__main__':
	labels, centroids = k_means(X=X, k=4)
	plot_data(X, labels)
	plot_centers(centroids)