一、三对角矩阵
1.三对角矩阵概念

2.三对角矩阵元素数量
对于给定n阶方阵M,若其为三对角矩阵,则元素个数N为:
- 若
n=1,此时方阵只有一个元素M[0][0],由定义知该元素也在三对角线上。故N=1。 - 若
n>1,由三对角矩阵特点知,矩阵的第一行和最后一行(第n行)分别有两个非零元素,其余行每行各有三个非零元素。故N = 3*(n-2)+2*2 = 3n-2。
综上,
N
=
{
1
,
n=1
3
n
−
2
,
n>1
N=\left\{ \begin{aligned} & 1 ,&\text{n=1}\\ & 3n-2, &\text{n>1}\\ \end{aligned} \right.
N={1,3n−2,n=1n>1
3.三对角矩阵下标变换推导(行优先和列优先)
对于给定n阶三对角方阵M和存放该方阵的数组A,非零元素M_ij(1≤i,j≤n,|i-j|≤1)同数组元素A[k](0≤k<N)存在一一对应的关系。下面分别推导从下标i,j到k和k到i,j的关系。
3.1行优先
- 从
M_ij到A[k]:即已知i,j要找出对应的k,需要知道,在数组A中,元素M_ij之前存放的元素个数num,则M_ij存放在A的第num+1个位置,对应数组A的下标正好为num(假设数组下标从0开始)。
- 先考虑
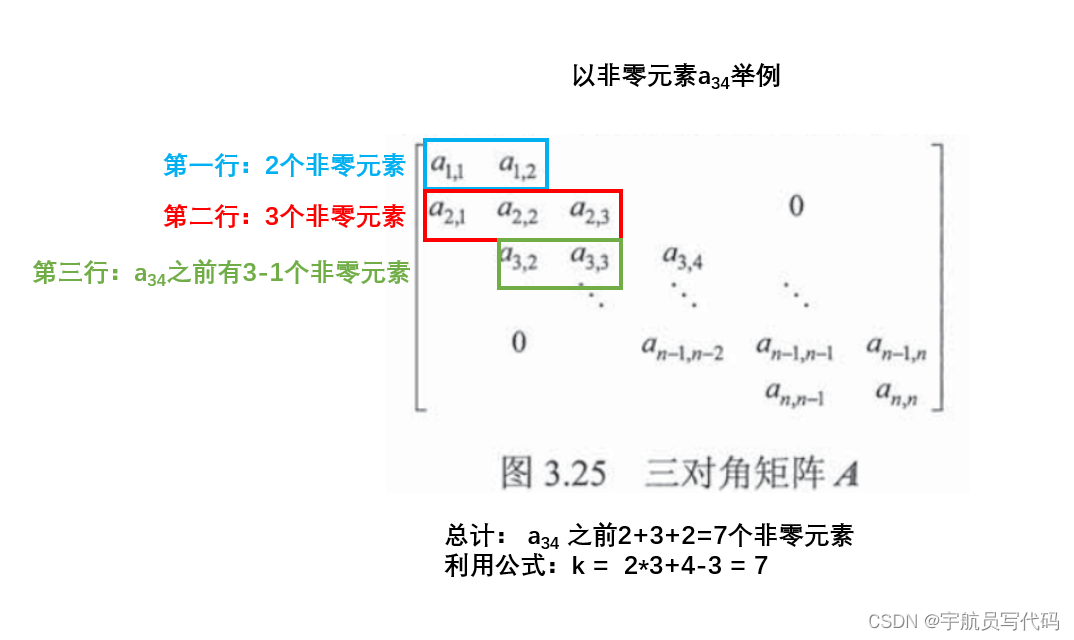
i>1的情况,即寻找第一行以下的非零元素M_ij:-
第一行有
2个非零元素;之后的2~i-1行,每行有三个非零元素。 -
第
i行,在M_ij之前的非零元素有j-(i-1)个。
-
故k = num = 2+3*(i-1-1)+j-(i-1)=2i+j-3。
- 而当
i=1时,有j=1或2。且A[0]=M_11,A[1]=M_12。代入发现也符合上述公式。
- 从
A[k]到M_ij。
首先求出A[k]位于M的第几行:由于M的第一行有两个元素,2~i-1行有三个元素,由此可以得到i关于k的表达式:i = ⌊(k+1)/3+1⌋(下取整)。(i+1为第一行“补”一个元素,加一是因为i从1开始)。
然后可以根据上面得到的k与i,j的关系得到:j = k-2i+3 。
3.列优先
由于三对角矩阵具有良好的对称性,所以只需要对行优先推导得到的关系中i,j互换即可。
即:
k=2j+i-3,j=⌊(k+1)/3+1⌋(下取整),i=k-2j+3。
二、C++实现三对角矩阵代码
//diagonalMatrix.hpp
#pragma once
#include "assert.h"
#include <iostream>
template <typename E>
// 检查下标越界
#define CHECK(i, j) \
assert(i >= 1 && j >= 1 && i <= m_dimension && j <= m_dimension);
// 检查是否是对角阵中的非零元素
#define IS_ZERO(i, j) abs(i - j) > 1
// 根据行/列优先原则获取数组对应下标
#define GET_IDX(i, j) m_priority ? (2 * i + j - 3) : (2 * j + i - 3)
class DiagonalMatrix
{
private:
int m_dimension; // 方阵阶数
int m_capacity; // 数组容量,即方阵中非零元素数量
E *m_array; // 存储方阵的数组
bool m_priority; // 0: 行优先 1:列优先
public:
DiagonalMatrix(int dimension, bool priority = false) : m_dimension(dimension), m_priority(priority)
{
assert(dimension >= 1);
if (dimension == 1)
m_capacity = 1;
else
m_capacity = 3 * dimension - 2; // capacity = (d - 2)*3 + 2*2 = 3d -2
m_array = new E[m_capacity];
}
~DiagonalMatrix()
{
delete m_array;
m_array = nullptr;
}
// 设置元素M_ij
void set(const E &element, int i, int j)
{
CHECK(i, j);
if (IS_ZERO(i, j))
return;
m_array[GET_IDX(i, j)] = element;
}
// 获取元素M_ij
E get(int i, int j)
{
CHECK(i, j);
if (IS_ZERO(i, j))
return 0;
return m_array[GET_IDX(i, j)];
}
// 获取数组元素A[k]对应方阵的下标i和j
void getKIdx(int k, int &i, int &j)
{
assert(k >= 0 && k < m_capacity);
if (!m_priority)
{
i = (k + 1) / 3 + 1;
j = k - 2 * i + 3;
}
else
{
j = (k + 1) / 3 + 1;
i = k - 2 * j + 3;
}
}
// 打印方阵
void printMatrix()
{
for (int i = 1; i <= m_dimension; i++)
{
for (int j = 1; j <= m_dimension; j++)
std::cout << get(i, j) << ' ';
std::cout << '\n';
}
}
int getCapacity()
{
return m_capacity;
}
int getDimension()
{
return m_dimension;
}
};
使用:
#include "diagonalMatrix.hpp"
int main()
{
using namespace std;
DiagonalMatrix<int> d(6);
int matrix[6][6] =
{
{1, 1, 0, 0, 0, 0},
{1, 1, 1, 0, 0, 0},
{0, 1, 1, 1, 0, 0},
{0, 0, 1, 1, 1, 0},
{0, 0, 0, 1, 1, 1},
{0, 0, 0, 0, 1, 1}};
// set value
int i, j, k;
for (i = 0; i < 6; i++)
for (j = 0; j < 6; j++)
if (matrix[i][j] != 0)
d.set(matrix[i][j], i + 1, j + 1);
// get idx and value
for (k = 0; k < d.getCapacity(); k++)
{
d.getKIdx(k, i, j);
printf("k = %d , i = %d, j = %d , matrix[%d][%d] = %d\n", k, i, j, i, j, d.get(i, j));
}
d.printMatrix();
}
结果:
k = 0 , i = 1, j = 1 , matrix[1][1] = 1
k = 1 , i = 1, j = 2 , matrix[1][2] = 1
k = 2 , i = 2, j = 1 , matrix[2][1] = 1
k = 3 , i = 2, j = 2 , matrix[2][2] = 1
k = 4 , i = 2, j = 3 , matrix[2][3] = 1
k = 5 , i = 3, j = 2 , matrix[3][2] = 1
k = 6 , i = 3, j = 3 , matrix[3][3] = 1
k = 7 , i = 3, j = 4 , matrix[3][4] = 1
k = 8 , i = 4, j = 3 , matrix[4][3] = 1
k = 9 , i = 4, j = 4 , matrix[4][4] = 1
k = 10 , i = 4, j = 5 , matrix[4][5] = 1
k = 11 , i = 5, j = 4 , matrix[5][4] = 1
k = 12 , i = 5, j = 5 , matrix[5][5] = 1
k = 13 , i = 5, j = 6 , matrix[5][6] = 1
k = 14 , i = 6, j = 5 , matrix[6][5] = 1
k = 15 , i = 6, j = 6 , matrix[6][6] = 1
1 1 0 0 0 0
1 1 1 0 0 0
0 1 1 1 0 0
0 0 1 1 1 0
0 0 0 1 1 1
0 0 0 0 1 1