联通性检测用途

• 照片中的像素
• 网络中的计算机
• 社交网络中的朋友
• 计算机芯片中的电路元器件
• 数学集合中的元素
• Fortan程序中的变量
• 复合体系中的金属位
  

假定已连接等价于

• 反身的: p与p本身是连接的.
• 对称的: 如果p连接到q,那么q也链接到p
• 传递的: 如果p连接到q并且q连接到r,那么p连接到r.

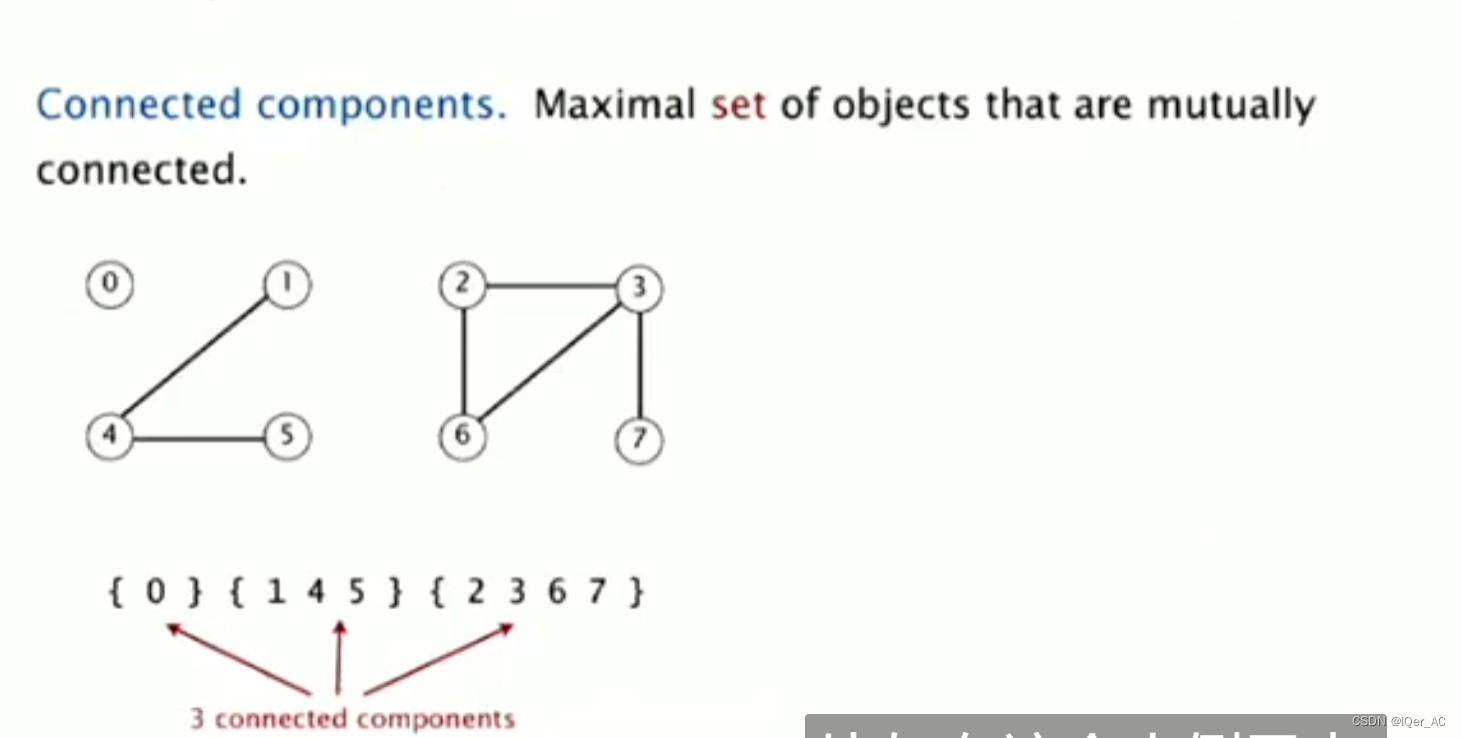
连接的组成

Union-find数据类型(API)

目标:为union-find设计有效的数据结构

• 对象N的数量可能是巨大的
• 操作次数M可能是巨大的
• 查找操作和union链接操作可能是混合在一起的

type UF struct
func (uf UF)NewUF(N int) 使用N个对象(0-N-1)初始化union-find数据结构
func union(p, q int) 在p和q之间添加连接
func connected(p, q int) 判断p和q是否相连

动态连接客户端

• 从标准输入stdin中读取输入
• 重复:
  1.从标准输入获取整数对
  2.如果他们不相连, 连接他们并打印这一对数字

package main

import (
	"bufio"
	"os"
	"strconv"
	"strings"

	"github.com/iqer/algo4_go/algs4"
)

func main() {
	scanner := bufio.NewScanner(os.Stdin)
	scanner.Scan()

	n, _ := strconv.Atoi(scanner.Text())
	uf := algs4.NewUF(n)
	for scanner.Scan() {
		line := scanner.Text()
		values := strings.Split(line, " ")
		p, _ := strconv.Atoi(values[0])
		q, _ := strconv.Atoi(values[1])
		uf.Union(p, q)
	}
}

quick-find 一种贪心算法

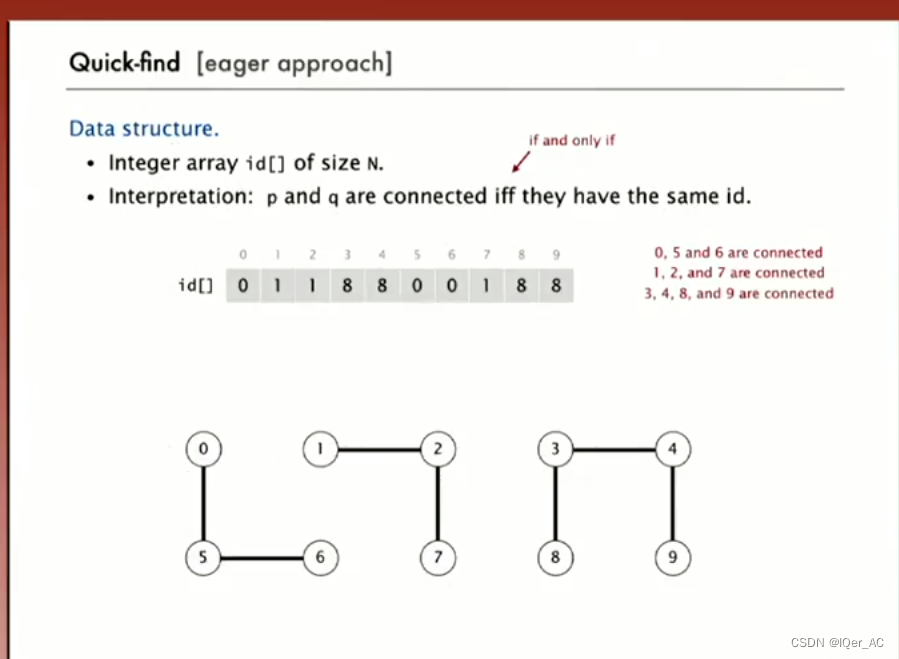
不同的点只有当在数组中的项是一样的时候, 那么他们是连通的.
校验p和q是否有相同的id

quick-find的实现

func NewUF(n int) *UF {
	uf := UF{n: n}
	uf.id = make([]int, n)
	// 将读取到的数字存在于一个数组中
	// 每个索引就代表着一个数
	// 索引对应的值就是连通的点的索引值
	// 之后如果不同索引位置上的值相同, 就代表这些索引位置代表的点是连通的
	for i := 0; i < n; i++ {
		uf.id[i] = i
	}
	return &uf
}

func (uf *UF) connected(p, q int) bool {
	return uf.id[p] == uf.id[q]
}

func (uf *UF) Union(p, q int) {
	pid := uf.id[p]
	qid := uf.id[q]
	for i := 0; i < len(uf.id); i++ {
		if uf.id[i] == pid {
			uf.id[i] = qid
		}
	}
}

分析算法效率

算法	初始化	union操作	find查找操作
快速查找	O(N)	O(N)	1

尝试一种快速合并的算法

一种’懒的方法’, 尽量避免计算直到不得不进行计算

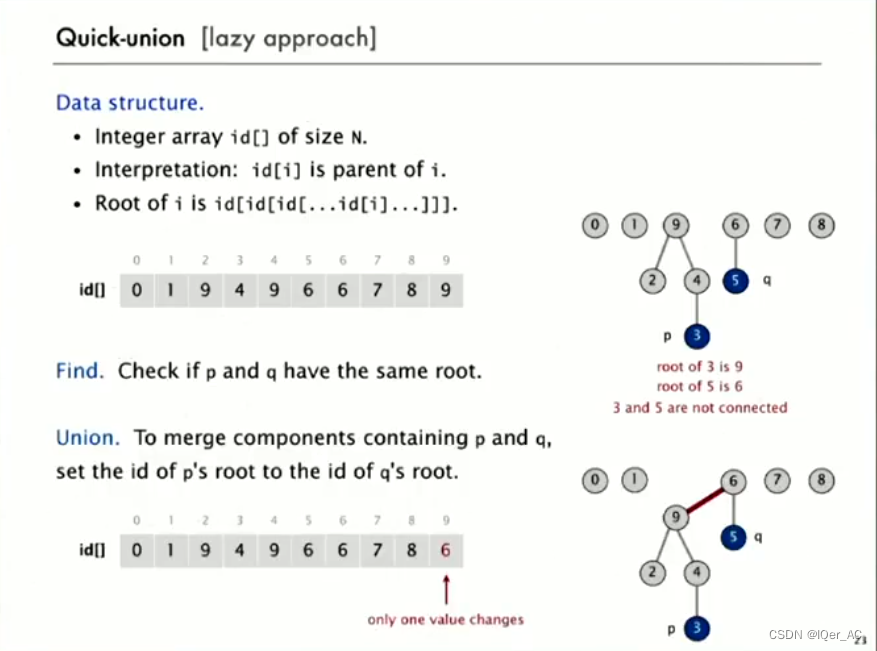
依然使用数组, 不过将其看作一组树即一片森林的表示.
Find查找操作就变成寻找两者是否拥有同样的parent节点, 如果有就是相连的.
这样做调整时, 只需要将p的根节点指向q的根节点, 就可以了.

func (uf *UF) root(i int) int {
	for i != uf.id[i] {
		i = uf.id[i]
	}
	return i
}

func (uf *UF) connected(p, q int) bool {
	return uf.id[p] == uf.id[q]
}

func (uf *UF) Union(p, q int)  {
	i := uf.root(p)
	j := uf.root(q)
	uf.id[i] = j
}

分析对比一下 quick-union还是太慢了

算法	初始化	union操作	find查找操作
quick-find	O(N)	O(N)	1
quick-union	o(N)	O(N)	O(N)

quick-find劣势

• Union操作代价高昂(N维路径)
• 树时平的, 但维持他们保持平的代价很高

quick-union劣势

• 树变高了
• 查找操作复杂度很高(可能是N维操作)

对quick-union的改进

改进方式1: 权重

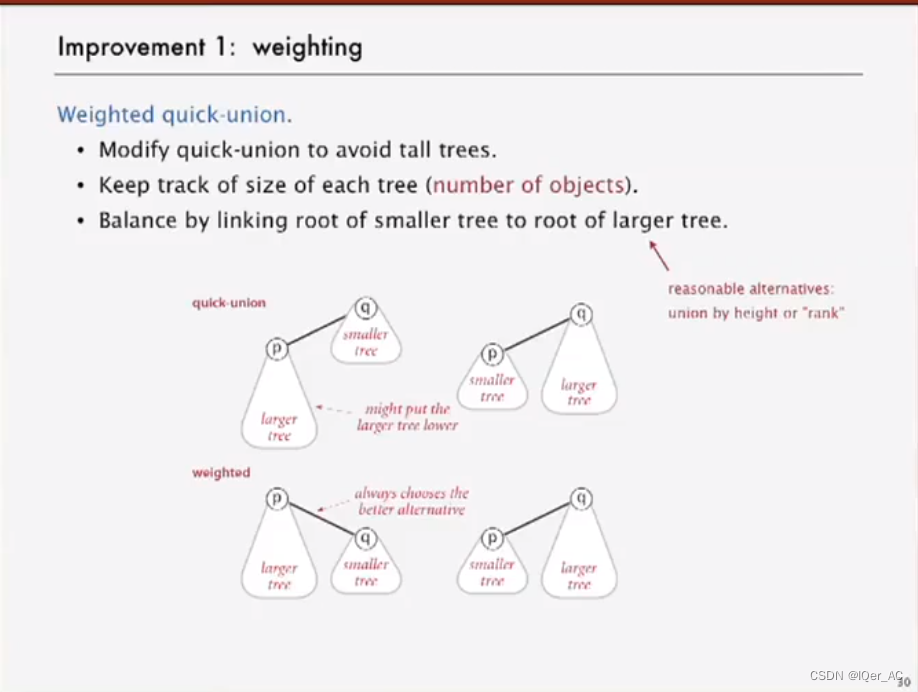
避免将更大的树放在低位

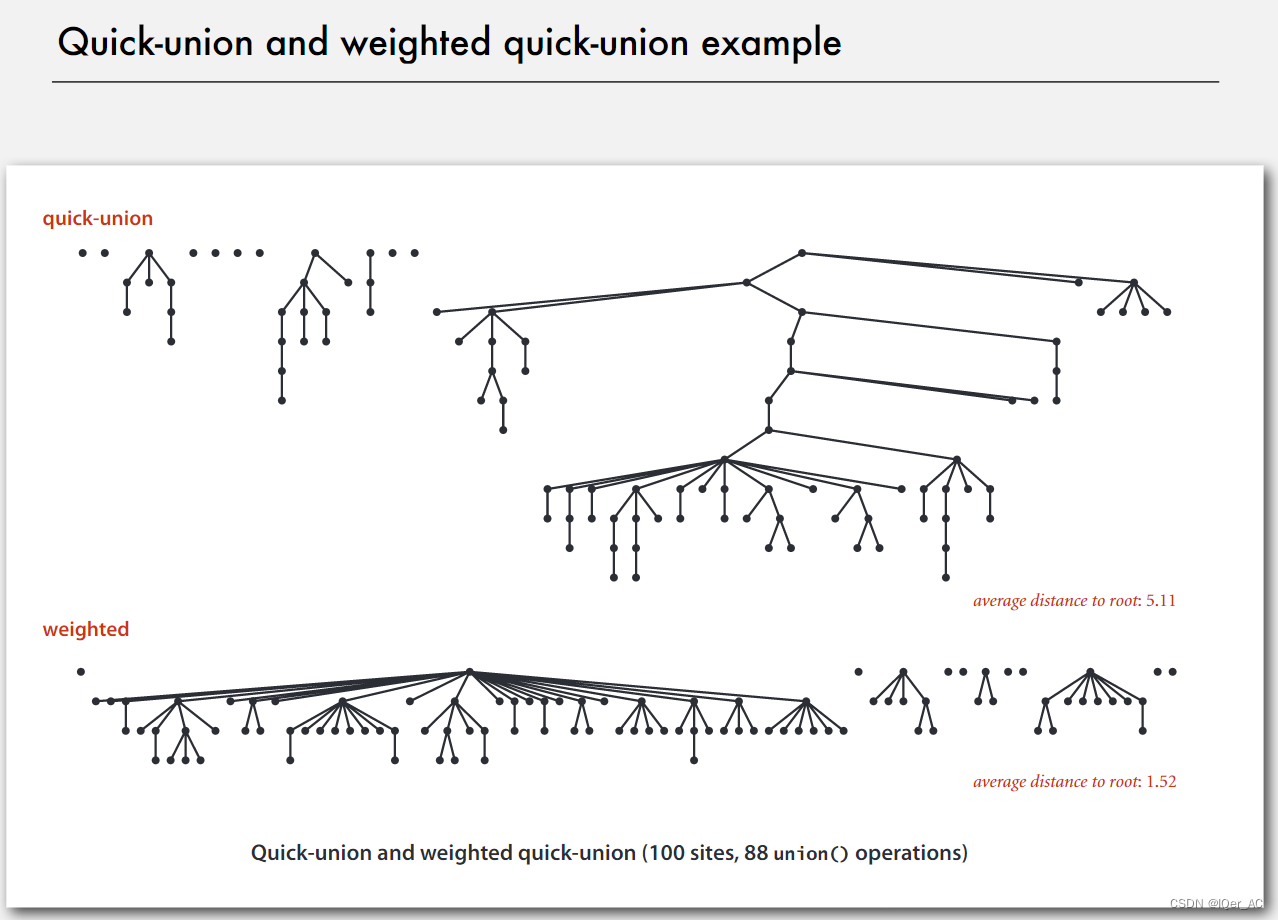
上图对比普通的quick-union操作和带权重的union操作, 可以看到带权重的操作对树高有所控制.

package algs4

type UF struct {
	id   []int
	n    int
	size map[int]int
}

func NewUF(n int) *UF {
	uf := UF{n: n}
	uf.id = make([]int, n)
	uf.size = map[int]int{}
	// 将读取到的数字存在于一个数组中
	// 每个索引就代表着一个数
	// 索引对应的值就是连通的点的索引值
	// 之后如果不同索引位置上的值相同, 就代表这些索引位置代表的点是连通的
	for i := 0; i < n; i++ {
		uf.id[i] = i
		uf.size[i] = 1
	}
	return &uf
}

func (uf *UF) root(i int) int {
	for i != uf.id[i] {
		i = uf.id[i]
	}
	return i
}

func (uf *UF) connected(p, q int) bool {
	return uf.root(p) == uf.root(q)
}

// improved quick-union

func (uf *UF) Union(p, q int) {
	i := uf.root(p)
	j := uf.root(q)
	if i == j {
		return
	}
	if uf.size[i] < uf.size[j] {
		uf.id[i] = j
		uf.size[j] += uf.size[i]
	} else {
		uf.id[j] = i
		uf.size[i] += uf.size[j]
	}
}

树高在logN

分析带权重的quick-union

算法	初始化	union操作	find查找操作
quick-find	O(N)	O(N)	1
quick-union	o(N)	O(N)	O(N)
带权重的QU	N	logN	logN

继续的改进方式2: path compression路径压缩

func (uf *UF) root(i int) int {
	for i != uf.id[i] {
		// 路径压缩, 使得每一个节点挂到它的祖父辈节点下
		uf.id[i] = uf.id[uf.id[i]]
		i = uf.id[i]
	}
	return i
}

算法性能对比

算法	最差情况耗时
quick-find	MN
quick-union	MN
weighted QU	N+MlogN
QU+path compression	N+MlogN
weighted QU + path compression	N+MlogN

Union-Find的应用场景