编辑

1. 单值二叉树

题目

题目分析

代码实现

不带返回值版本

带返回值版本

递归展开图

2. 相同的树

题目

题目分析

代码实现

3. 对称二叉树

题目

题目分析

代码实现

4. 另外一颗子树

题目

题目分析

代码实现

递归展开图

5. 二叉树的前、中、后序遍历

5.1 二叉树的前序遍历

题目

题目分析

代码实现

注意点

1. 单值二叉树

题目

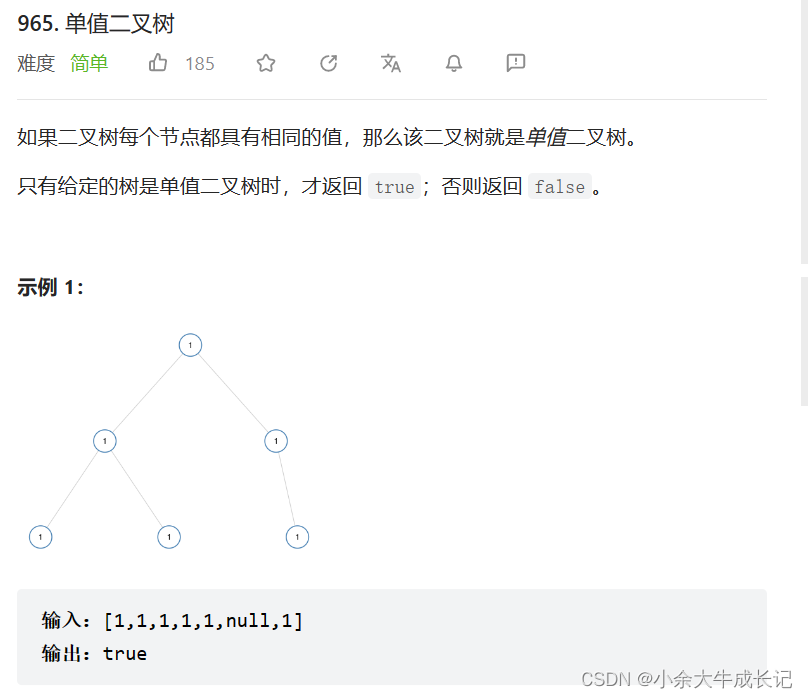
题目分析

我们在这里首先想到的还是用遍历的想法来实现，把整个数都遍历一遍，看看有没有和val不相等的值，我们这时也可以发现前序遍历比较实用（一来就访问他的根，再访问他的左右孩子）

代码实现分析：

1. 首先在主函数中首先使用if条件判断，判断树的根节点是不是空，是空，就返回true（没有违背单值二叉树的定义）

2. 调用前序遍历，实现前序遍历函数

3. 前序遍历函数中，也要判断父亲节点是不是空，是空就回退到调用左儿子的地方，开始递归调用右孩子,直到遍历完整颗树，都没找到，或者是找到不同的值，一层一层的返回上去.....

易错点1：我们在找到的时候，回退出递归的时候，由于我们回退到的是上一层的左节点，这时即使找到了不同的值，我们还要进行右子树递归，这时就显得非常多余，如何改进呢？

方法：我们发现在前序遍历函数中的if判断条件可以完善一下

易错点2：我们这里先写的是不带返回值的，我们定义了一个全局的flag，先将flag初始化为true，后面如果不是单值二叉树的话，我们又将flag改为false，但是我们提交的时候，会有测试用例跑步过去，其实就是这里定义全局flag的问题，这里假如前一棵树不是单值二叉树（flag=false），但是这时第二次调用单值二叉树的时候，本来输出的结果是true，但是这时却输出false，显然是有问题的，怎么解决呢？

方法：在主函数调用前序遍历函数的前面，每次将flag初始化为true

代码实现

不带返回值版本

bool flag=true;
void PreOrderCompare(struct TreeNode* root ,int val)
{
    
   if(root == NULL || flag ==false)//这里的判断条件flag==false就是（易错点1）说的
    return;

    if(root->val !=val)
    {
        flag=false;
        return;//这里是找到了不同的值，就不要往下递归了，直接开始回退了
    }  
 
    PreOrderCompare(root->left,val);
    PreOrderCompare(root->right,val);

}

bool isUnivalTree(struct TreeNode* root){
      if(root == NULL)
      return true;

      flag=true;//每次调用前序遍历，都要将flag初始化为true（易错点2）
      PreOrderCompare(root,root->val);
      return flag;
}

带返回值版本

这里可以采用数学的交换律

a=b 、b=c ——> a=c

每个节点和自己的左右孩子比较，左右孩子又和自己的左右孩子比较，一直遍历完。。。。

bool isUnivalTree(struct TreeNode* root){
      if(root == NULL)
      return true;

      if(root->left && root->left->val != root->val)
      return false ;  
      
      if(root->right && root->right->val != root->val)
      return false ;

      return isUnivalTree(root->left)
      && isUnivalTree(root->right);
}

递归展开图

2. 相同的树

题目

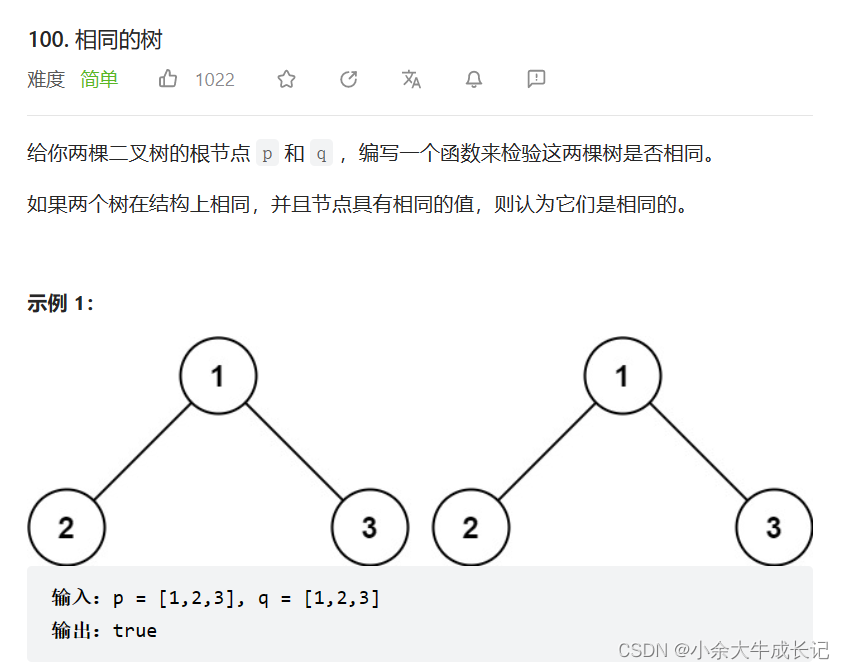
题目分析

题目是比较两棵树是否相同，也就是看两棵树所有节点的数据是不是相同，这时其实还是采用同时遍历两颗树的方法进行比较，这时就有一下三种情况需要分别处理：

1. 当两颗树都是空的情况，返回true

2. 当两棵树一颗为空，另一颗不为空的时候，就直接返回false

3. 走到这里证明两棵树都不为空，这时比较数据，采用同时递归两棵树的方式进行比较，只有比较到不同的情况，返回false，否则就一直遍历，如果直到遍历完都没又不同的数据，那这两棵树就是相同的了

代码实现

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
      if(p==NULL && q==NULL)
      return true;

      if(p == NULL || q == NULL)
      return false;   
 
      if(p->val != q->val) 
      return false; 
     
    return isSameTree(p->left,q->left)
        && isSameTree(p->right,q->right);
}

3. 对称二叉树

题目

题目分析

题目的意思是判断这颗二叉树是不是对称的，我们发现可以将这颗二叉树分成两个子树进行比较，分别递归比较左子树的left和右子树的right、左子树的right和右子树的letf，如果比较晚了，都一样，那就是对称二叉树

实现步骤：

1. 先判断根节点是不是NULL，是，就返回true

2. 根节点不为NULL，再判断左右孩子节点是不是同时为NULL，如果是，那就返回true

3. 走到这里，那就是左右孩子不同时为空，但是有一个为空，那就返回false

4. 走到这里，那就是左右孩子都不为NULL，那就开始比较节点中的数据，如果不相等，那就返回false

5. 走到这里，那就是左右孩子节点数据相等，就开始递归左孩子节点的left节点和右孩子的right节点、递归左孩子的right节点和右孩子的left节点，两个比较都返回true，这时这颗二叉树才是对称的，否则就不对称

代码实现

bool isSymmetricsSubTree(struct TreeNode* root1,struct TreeNode* root2)
  {
       if(root1 == NULL && root2 ==NULL)
       return true;
       
       if(root1 == NULL || root2 == NULL)
       return false;

       if(root1->val != root2->val)
        return false;

        return isSymmetricsSubTree(root1->left,root2->right)
            &&  isSymmetricsSubTree(root1->right,root2->left); 
  }

bool isSymmetric(struct TreeNode* root){
    if(root == NULL)
    return true;
    
    return isSymmetricsSubTree(root->left, root->right);
}

4. 另外一颗子树

题目

题目分析

题目的意思其实是判断主树中是否有和子树相同的二叉树，这里还是采用遍历的思路

实现步骤：

1. 先判断主树的根节点是不是NULL，是，那就直接返回false

2. 不是NULL，那就开始递归遍历，这是我们可以用这样的方法，把主树的每个节点都和子树递归比较，也就是前面判断两棵树是不是相同的二叉树的方法(2.相同二叉树）

3. 如果同时遍历比较两棵树，isSameTree返回的是true，那证明两棵树完全一样，如果不一样，我们这是开始递归isSubtree，把根节点换成左孩子节点和子树进行比较，不相同，那就开始递归遍历比较右孩子节点和子树，直到将主树的所有节点都和子树进行比较了， isSameTree都没有返回true，那就是主树里面没有和子树一样的子二叉树

代码实现

注意1：这里的isSubtree返回的是左孩子比较结果 || 右孩子比较结果，也就是左右孩子有一个和子树一样，就返回true

注意2 ：这里的isSubtree的返回值，是靠isSameTree带回的

举例：假如遍历比较完了一个根节点的左孩子，这时返回的是false，然后开始遍历这个根节点的右孩子，这是返回的是true，false || true 这时返回的是true

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
      if(p==NULL && q==NULL)
      return true;

      if(p == NULL || q == NULL)
      return false;   
 
      if(p->val != q->val) 
      return false; 
     
    return isSameTree(p->left,q->left)
        && isSameTree(p->right,q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){

    if(root == NULL)
      return false;
    
    if(isSameTree(root,subRoot))
    return true;

    return isSubtree(root->left,subRoot)
        || isSubtree(root->right,subRoot);

}

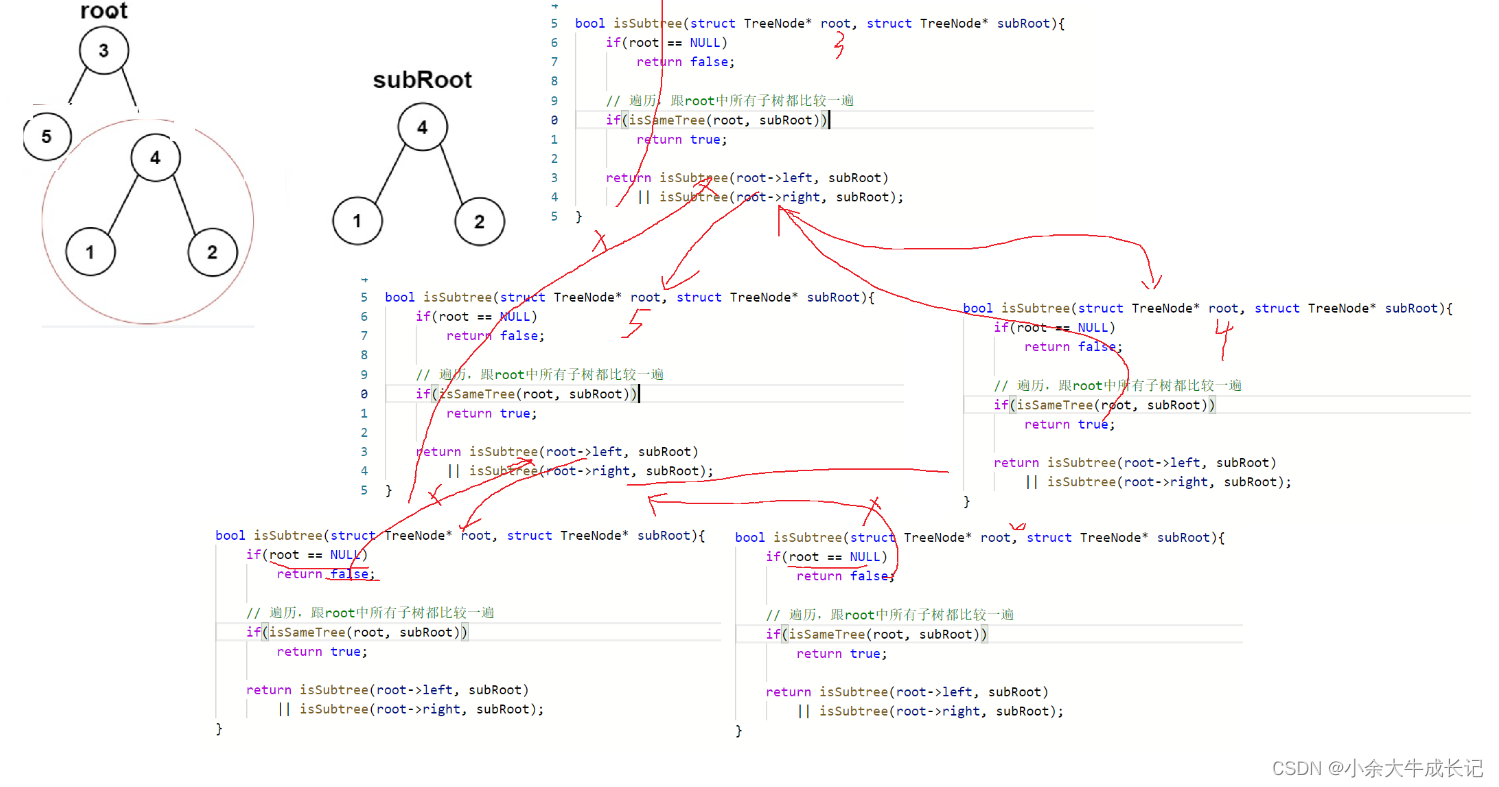
递归展开图

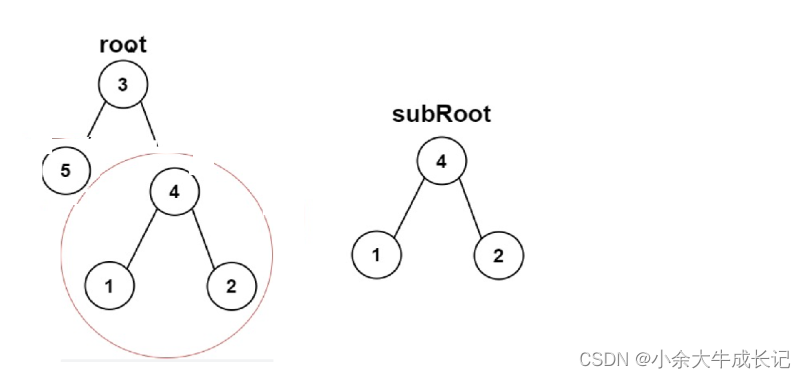
以上面的示例画递归展开图

5. 二叉树的前、中、后序遍历

5.1 二叉树的前序遍历

题目

题目分析

题目的意思是遍历这颗二叉树，并把前序遍历的结果放到一个数组里面返回，那这个数组需要是malloc出来的

代码实现步骤：

1. 先判断这颗二叉树的根节点是否为空，为空，直接就return

2. 如果不是NULL，那这时就创建一个子函数，用来返回这个二叉树有多少个节点，然后再动态开辟一个数组用来存数据

3. 再创建一个子函数，用来前序遍历这个二叉树，把数据存储到开辟的空间中，最后返回出去

代码实现

int Treesize (struct TreeNode* root)
{
    return root == NULL ? 0 : Treesize(root->left) + Treesize(root->right) + 1;
} 

void preorder (struct TreeNode* root, int* a , int* pi)
{
    if(root == NULL)
      return ;
    
    a[(*pi)++] = root->val;
    preorder(root->left, a, pi);
    preorder(root->right, a, pi);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize){
    
    *returnSize = Treesize(root);
    int* a=(int*)malloc(*returnSize * sizeof(int));

     int i=0;
     preorder(root, a, &i);

    return a;
}

注意点

上面的代码中，我们传数组a的下标，采用了传指针的方式，为什么呢？（局部变量的原因）

因为在像下面的举例中，我们可以发现，在递归调用存储完3的时候i=2，然后i++，这时的i就变成了3，但是这时遍历3的左右孩子节点的时候发现都为空，这时2的左节点遍历就结束了，就开始右递归，但是本来i为3，但是在返回后，由于i是局部变量，i的值在2递归右孩子节点的函数中是2，但是这时又要存储节点4里的数据，这时前面存储的3就会被2覆盖掉，然后i++，后面就会有一个空的元素，执行就是随机值

觉得文字太多，直接看下面的递归展开图！！！！