✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机  电力系统

⛄ 内容介绍

一种变分贝叶斯的非线性卡尔曼滤波器的设计方法,涉及滤波器领域,本发明首先在高斯假设条件下构造逼近后验概率密度函数的变分分布,并以KL散度作为惩罚函数以实现状态估计的迭代逼近,继而根据变分贝叶斯框架以置信下界最大为目标函数推导出一种变分贝叶斯的非线性卡尔曼滤波器.本发明能够获得非线性状态后验概率密度函数更"紧"的逼近形式,从而提高状态估计精度,可以实现系统状态估计过程中后验概率密度函数积分的难以求解问题转化为优化ELBO下界的问题,并且将自适应加权的KL散度作为惩罚函数以提高优化的灵活性,从而改善状态估计精度,对于非线性状态估计理论和实际工程应用具有非常重要的意义.

⛄ 部分代码

function C = utchol(P)

%

% 

% M. S. Grewal & A. P. Andrews

% Kalman Filtering Theory and Practice Using MATLAB

% Third Edition, Wiley & Sons, 2008

% 

% for P symmetric and positive definite,

% computes upper triangular C such that

% C*C' = P

%

[n,m] = size(P);

if (n-m) error('non-square argument'); end;

  for j=m:-1:1,

    for i=j:-1:1,

    sigma = P(i,j);

      for k=j+1:m,

      sigma = sigma - C(i,k)*C(j,k);

      end;

    C(j,i) = 0;

      if (i==j)

        C(i,j) = sqrt(max([0,sigma]));

      elseif (C(j,j) == 0)

        C(i,j) = 0;

      else

        C(i,j) = sigma/C(j,j);

      end;

    end;

  end;

      

⛄ 运行结果

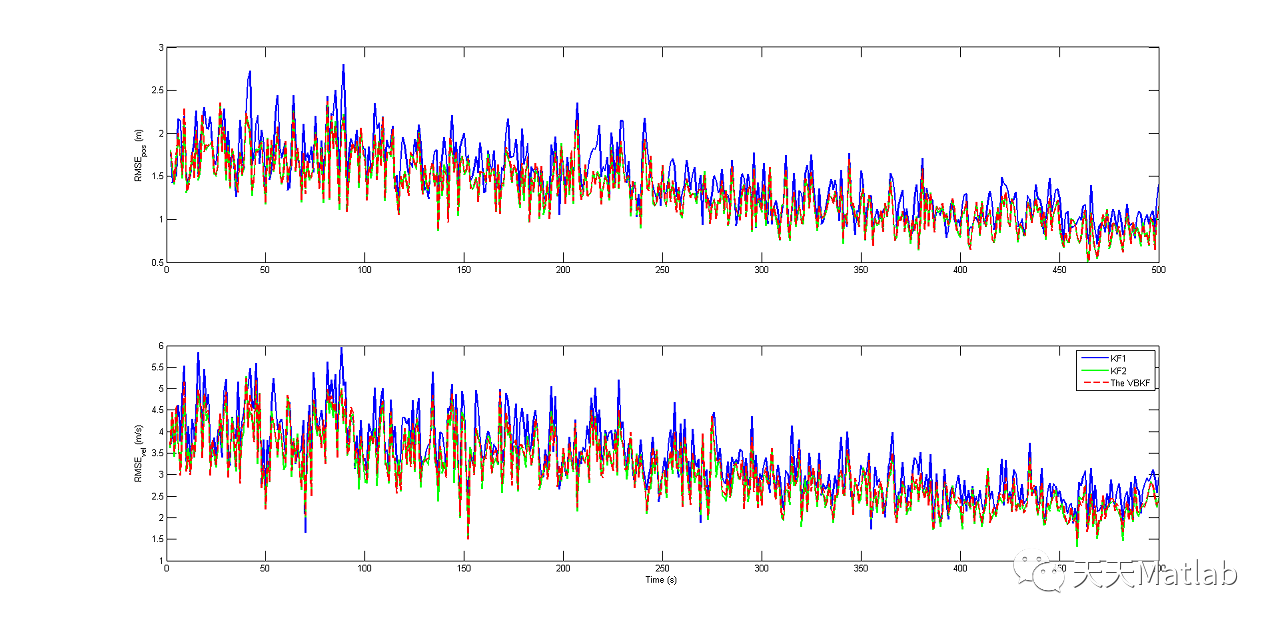
⛄ 参考文献

[1]兰华, 胡玉梅, 王增福,等. 一种变分贝叶斯的非线性卡尔曼滤波器的设计方法:, CN108599737A[P]. 2018.

⛄ Matlab代码关注

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料