【POJ No. 3468】 简单的整数问题 A Simple Problem with Integers

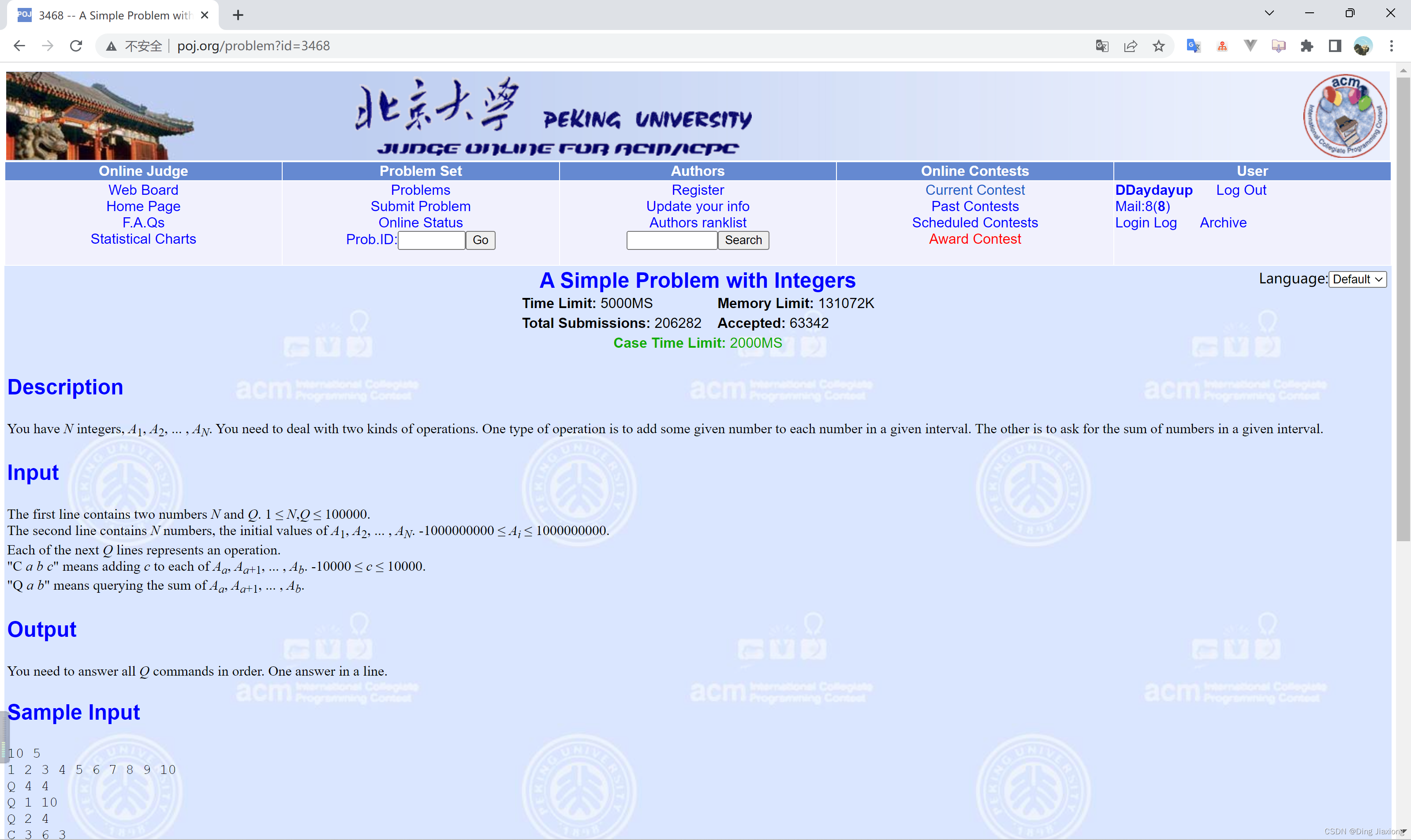
北大OJ 题目地址

其实这道题之前也已经 做过了

https://blog.csdn.net/weixin_44226181/article/details/128112081

上次就 直接用的区间更新 和区间查询。这次 我们使用 分块方法实现一次。

【题意】

有N 个整数A 1, A 2, …, AN ，需要对其进行两种操作，一种操作是对给定区间中的每个数都添加一个给定的数，另一种操作是查询给定区间中数的总和。

【输入输出】

输入：

第1行包含两个数N 和Q （1≤N ，Q ≤105 ）；第2行包含N 个数，为A 1 , A 2 , …, AN 的初始值（-109 ≤Ai ≤109 ）；接下来的Q 行，每行都表示一种操作，“C a b c ”表示将Aa , Aa +1 ,…, Ab 中的每一个数都加c （-104 ≤c ≤104 ），“Q a b ”表示查询Aa , Aa +1 , …, Ab 的总和。

输出：

对每个查询，都单行输出区间和的值。

【样例】

提示：总和可能超过32 位整数 的范围。

【思路分析】

这道题有两种操作：区间更新和区间查询，可采用分块算法解决。

【算法设计】

① 分块预处理。将序列分块，然后对每个块都标记左右端点L[i]和R[i ]，对最后一块需要特别处理；标记每个元素所属的块，累加每一块的和值。

② 区间更新。首先取l 和r 所属的块，p =pos[l ]，q =pos[r]；若属于同一块，则对该区间的所有元素都进行暴力修改，同时更新该块的和值。若不属于同一块，则对中间完全覆盖的块打上懒标记，add[i ]+=d ；对首尾两端的元素暴力修改即可。

③ 区间查询。首先取l 和r 所属的块，p =pos[l ]，q =pos[r]；若属于同一块，则对该区间的所有元素都进行暴力累加，然后加上懒标记上的值。若不属于同一块，则对中间完全覆盖的块累加sum[]值和懒标记上的值，然后对首尾两端的元素暴力累加元素值及懒标记值。

【算法实现】

#include<cstdio>
#include<algorithm>
#include<cmath>
#define ll long long
#define N 100010

using namespace std;

ll a[N],sum[N],add[N];
int L[N],R[N],d;
int pos[N];
int n,m,t,l,r;
char op[3];

void build(){
	t=sqrt(n*1.0);//float sqrt (float),double sqrt (double),double long sqrt(double long)
			 //注意没有sqrt(int)，但是返回值可以为int
			 //也可以选择G++提交,否则int型做参数会提示编译问题 
    int num=n/t;
    if(n%t)  num++;
    for(int i=1;i<=num;i++){
        L[i]=(i-1)*t+1;//每块的左右 
        R[i]=i*t;
    }
    R[num]=n;
    for(int i=1;i<=num;i++)
		for(int j=L[i];j<=R[i];j++){
        	pos[j]=i;//表示属于哪个块
        	sum[i]+=a[j];//计算每块和值
		}
} 

void change(int l,int r,long long d){//区间[l,r]加上d 
    int p=pos[l],q=pos[r];//读所属块 
    if(p==q){//在一块中
        for(int i=l;i<=r;i++)//暴力修改 
			a[i]+=d;
        sum[p]+=d*(r-l+1);//修改和值 
    }
    else{
        for(int i=p+1;i<=q-1;i++)//中间完全覆盖块打懒标记 
			add[i]+=d;
        for(int i=l;i<=R[p];i++)//左端暴力修改 
			a[i]+=d;
        sum[p]+=d*(R[p]-l+1);
        for(int i=L[q];i<=r;i++)//右端暴力修改
			a[i]+=d;
        sum[q]+=d*(r-L[q]+1);
    }
}

ll query(int l,int r){
    int p=pos[l],q=pos[r];
    ll ans=0;
    if(p==q){//在一块中
        for(int i=l;i<=r;i++)//累加 
			ans+=a[i];
        ans+=add[p]*(r-l+1);//计算懒标记 
    }
    else{
        for(int i=p+1;i<=q-1;i++)//累加中间块 
        	ans+=sum[i]+add[i]*(R[i]-L[i]+1);
        for(int i=l;i<=R[p];i++)//左端暴力累加
			ans+=a[i];
        ans+=add[p]*(R[p]-l+1);
        for(int i=L[q];i<=r;i++)//右端暴力累加
			ans+=a[i];
        ans+=add[q]*(r-L[q]+1);
    }
    return ans;
}

int main(){
	
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%lld",&a[i]);
    build(); 
    for(int i=1;i<=m;i++){
        scanf("%s %d %d",op,&l,&r);
        if(op[0]=='C'){
            scanf("%d",&d);
            change(l,r,d);
        }
        else
			printf("%lld\n",query(l,r));
    }
	
    return 0;
}