一、简介

图像风格迁移是指，将一副内容图的内容，和一幅或多幅风格图的风格融合在一起，从而生成一些有意思的图片。

我们使用 TensorFlow 和 Keras 分别来实现图像风格迁移，主要用到深度学习中的卷积神经网络，即CNN。

二、准备

安装包。

pip install numpy scipy tensorflow keras

再准备一些风格图片，和一张内容图片。

三、原理

为了将风格图的风格和内容图的内容进行融合，所生成的图片，在内容上应当尽可能接近内容图，在风格上应当尽可能接近风格图。因此需要定义 内容损失函数 和 风格损失函数，经过加权后作为总体损失函数。

实现步骤如下：
- 随机产生一张图片
- 在每轮迭代中，根据总体损失函数，调整图片的像素值
- 经过多轮迭代，得到优化后的图片

四、内容损失函数

两张图片在内容上相似，不能仅仅靠简单的纯像素比较。
CNN 具有抽象和理解图像的能力，因此可以考虑将各个卷积层的输出作为图像的内容。
以 VGG19 为例，其中包括了多个卷积层、池化层，以及最后的全连接层。

CNN是一类深度学习模型的统称，而VGG是其中一种经典的卷积神经网络模型，它在图像分类任务中表现出色，成为了深度学习模型的重要代表之一。

这里我们使用 conv4_2 的输出作为图像的内容表示，定义内容损失函数如下：

这是内容损失函数的公式表示，其中公式表示如下：

$\mathcal{L}_{content}(\vec{p}, \vec{x}, l) = \frac{1}{2} \sum_{i,j} (F_{ij}^l - P_{ij}^l)^2$

$\vec{p}$ 表示参考图片（即内容原图）
$\vec{x}$ 表示待转换成的图片（即生成的图片）
$l$ 表示卷积神经网络的层数
$F_{ij}^l$ 表示在第 $l$ 层卷积神经网络中
$\vec{x}$ 在位置 $(i, j)$ 的特征图
$P_{ij}^l$ 表示在第 $l$ 层卷积神经网络中
$\vec{p}$ 在位置 $(i, j)$ 的特征图。
公式表示的意义是，计算 $\vec{x}$ 和 $\vec{p}$ 在第 $l$ 层卷积神经网络中的特征图的差异，以此来衡量两张图片在该层的内容相似程度。因为这里使用了平方差，所以公式中还需要除以 2。

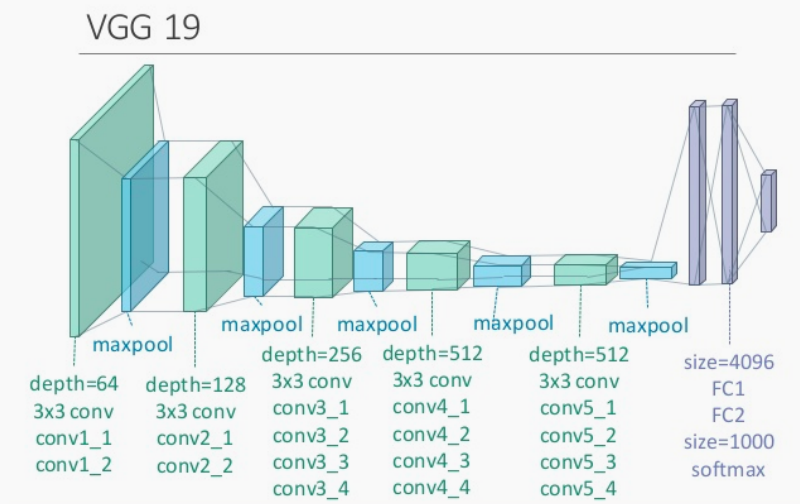
请添加图片描述

VGG是用于大规模分类任务的模型，这个模型已经是训练好的，所以里面的参数也是调好的了
图片是RGB三个维度，模型的输入是四维的tensor
1. 第一维：图片个数
2. 第二维：图片的高度
3. 第三维：图片的宽度
4. 图片的深度（即通道的个数，即特征图的个数）
一开始输入进来的维度，总体上看是比较“薄的”，形状像一本书一样，在这个过程中不断进行图像的抽象，通过不断卷积，宽度和高度不断变小，变得越来越厚（即深度变大，即通道数变多）。
一开始可能看到的是边缘、局部的区域，后面可以慢慢看到一些特征元素，比如：部分五官，甚至整个人脸。

五、风格损失函数

风格是一个很难说清楚的概念，可能是笔触、纹理、结构、布局、用色等等。

这里我们使用卷积层各个特征图之间的互相关作为图像的风格，以conv1_1为例：

共包含64个特征图即 feature map，或者说图像的深度、通道的个数；
每个特征图都是对上一层输出的一种理解，可以类比成64个人对同一幅画的不同理解
这些人可能分别偏好印象派、现代注意、超现实主义等不同风格
当图像是某一种风格时，可能这一部分人很欣赏，但那一部分人不喜欢
当图像是另一种风格时，可能这一部分人不喜欢，但那一部分人很欣赏
64个人之间理解的差异，可以用特征图的互相关表示，这里使用 Gram矩阵计算互相关

风格损失函数用于衡量两张图片之间的风格相似程度，可以用于图像风格转换等任务中。下面是风格损失函数的公式表示：

$\mathcal{L}_{style}(\vec{p}, \vec{x}) = \sum_{l=1}^{L} w_l \cdot \frac{1}{4N_l^2M_l^2} \sum_{i=1}^{N_l} \sum_{j=1}^{N_l} (G_{ij}^l - A_{ij}^l)^2$

$\vec{p}$ 表示参考图片（即内容原图）
$\vec{x}$ 表示待转换图片（即生成的图片）
$L$ 表示卷积神经网络的层数
$N_l$ 表示第 $l$ 层的特征图的通道数
$M_l$ 表示第 $l$ 层的特征图的高度和宽度的乘积
$G_{ij}^l$ 表示参考图片在第 $l$ 层的特征图中
位置 $(i, j)$ 的Gram 矩阵
$A_{ij}^l$ 表示待转换图片在第 $l$ 层的特征图中
位置 $(i, j)$ 的格拉姆矩阵
$w_l$ 表示第 $l$ 层所占的权重

Gram 矩阵的计算方法如下：

$G_{ij}^l = \sum_{k=1}^{M_l} F_{ik}^l \cdot F_{jk}^l$

$F_{ik}^l$ 表示参考图片在第 $l$ 层的特征图中，
位置 $(i, k)$ 的像素值
格拉姆矩阵表示的是特征图中各个通道之间的相关性。如果有64个特征图，那么 Gram矩阵的大小便是64 x 64，第i行第j列的值表示第i个特征图和第j个特征图之间的互相关，用内积计算。

风格损失函数的含义是，计算参考图片和待转换图片在卷积神经网络的不同层中的 Gram 矩阵之间的差异，以此来衡量两张图片之间的风格相似程度。因为使用了平均平方差，所以公式中没有除以 2。

六、总体损失函数

总体损失函数即内容损失函数和风格损失函数的加权，不同的权重会导致不同的迁移风格效果。

这是图像风格转换任务中的总损失函数，其中 $\vec{p}$ 表示参考图片， $\vec{a}$ 表示参考图片的风格， $\vec{x}$ 表示待转换图片， $\alpha$ 和 $\beta$ 是两个超参数，公式表示如下：

$\mathcal{L}_{total}(\vec{p}, \vec{a}, \vec{x}) = \alpha \cdot \mathcal{L}_{content}(\vec{p}, \vec{x}) + \beta \cdot \mathcal{L}_{style}(\vec{a}, \vec{x})$