离散系统函数零积点分析

在 Matlab中，系统函数的零极点就可以通过函数 roots 得到。

函数的零极点也可以通过函数 tf2zp 获得，其调用格式为：[Z, P, K] = tf2zp(B, A)，函数 tf2zp 可以将H(z)的有理分式转换为零极点增益形式，B、A分别表示 H(z) 的分子、分母多项式的系统向量，

Z 表示零点向量，P 表示极点向量，K 表示系统增益。

函数 zplane 用于绘制 H(z)的零极点图，其调用形式为：zplane(z, p)，绘制出列向量 z 中的零点(以符号 o 表示)和 p 中的极点(以符号 x 表示)。

说明：如果 z 和 p 为矩阵，则会以不同的颜色绘制出 z 和 p 各列中的零点和极点。

% E_6_5.m

% 已知某离散系统的系统函数如下。试用 Matlab 求出该系统的零极点，并画出零极点分布图，判断系统是否稳定。

% 系统函数为：H(z) = (2*z + 1)/(3*z^5 - 2*z^4 + 1)

% E_6_5.m
% 已知某离散系统的系统函数如下。试用 Matlab 求出该系统的零极点，
% 并画出零极点分布图，判断系统是否稳定。
% 系统函数为：H(z) = (2*z + 1)/(3*z^5 - 2*z^4 + 1)

% 绘制零极点分布图的实现程序
a = [3 -2 0 0 0 1];
b = [2 1];
% ljdt(a,b);
% % % % % % 函数ljdt % % START % % % % % % % % % % % % % % % % 
% function ljdt(A,B)
p = roots(a);  % 求系统极点
q = roots(b);  % 求系统零点
p = p';  % 将极点列向量转置为行向量
q = q';  % 将零点列向量转置为行向量
x = max(abs([p q 1]));  % 确定纵坐标范围
x = x + 0.1;
y = x;
hold on
axis([-x x -y y]);
w = 0:pi/300:2*pi;
t = exp(1i*w);
plot(t);  % 画出单位圆
axis('square');
plot([-x x], [0 0]);
plot([0 0], [-y y]);
text(0.1, x, 'jIm[z]');
text(y, 1/10, 'Re[z]');
plot(real(p), imag(p), 'x');
plot(real(q), imag(q), 'o');
title('零极点图');
hold off;
% end
% % % % % % % % 函数ljdt % % END % % % % % % % % % % % % % % % % 
p = roots(a)
q = roots(b)
pa = abs(p)

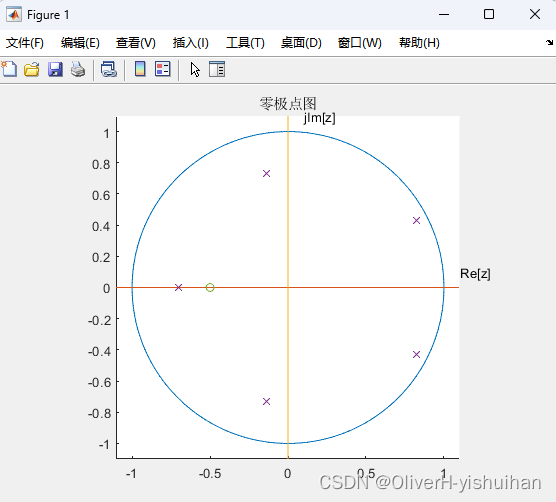
% 该系统的所有极点都位于 Z 平面的单位圆内，故该系统为稳定系统。