9.1 公倍数与公因数

利用 辗转相除法 ，我们可以很方便地求出两个数的最大公因数（gcd）；将两个数相乘再除以最大公因数就可以得到最小公倍数（lcm） 。

int gcd(int a, int b){
	return b == 0 ? a : gcd(b, a % b);
}
int lcm(int a, int b){
	return a * b / gcd(a, b);
}

进一步，我们也可以通过扩展欧几里得算法，在求出 a 和 b 的最大公因数的同时，也得到他们的系数 x 和 y ，从而使 ax + by = gcd(a, b) 。

int xGCD(int a, int b, int &x, int &y){
	if(!b){
		x = 1, y = 0;
		return a;	
	}
	int x1, y1, gcd = xGCD(b, a%b, x1, y1);
	x = y1, y = x1 - (a / b) * y1;
	return gcd;
}

9.2 质数

质数又称素数，指的是在大于 1 的自然数中，除了 1 和它本身以外不再有其他因数的自然数。 值得注意的是，每一个数都可以分解成为质数的乘积。

204.计数质数（中等）

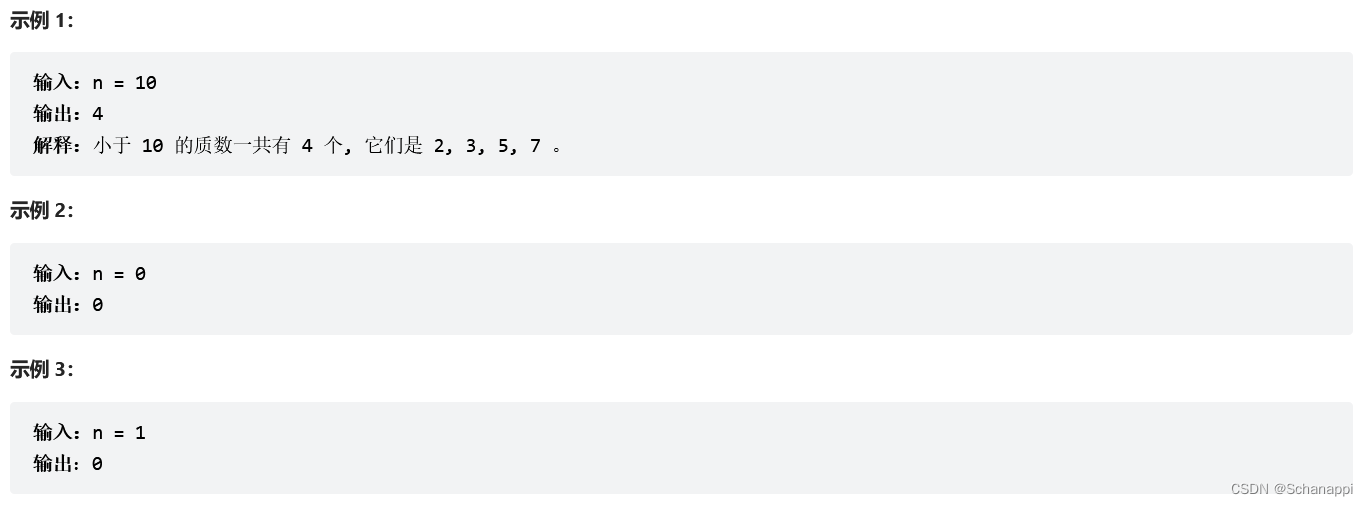
思路及代码： 204.计数质数

9.3 数字处理

504. 七进制数（简单）

思路及代码： 504. 七进制数

172. 阶乘后的零（中等）

思路及代码： 172. 阶乘后的零

415. 字符串相加（简单）

思路及代码： 415. 字符串相加

326. 3 的幂（简单）

思路及代码： 3 的幂

9.4 随机与取样

384. 打乱数组（中等）

思路及代码：384. 打乱数组

528. 按权重随机选择（中等）

思路及代码： 528. 按权重随机选择

382. 链表随机节点（中等）

思路及代码： 382. 链表随机节点

9.5 练习

168. Excel表列名称（简单）

思路及代码： 168. Excel表列名称

67. 二进制求和（简单）

思路及代码： 67. 二进制求和

238. 除自身以外数组的乘积（中等）

思路及代码： 238. 除自身以外数组的乘积

462.最小操作次数使数组元素相等 II（中等）

思路与代码： 462.最小操作次数使数组元素相等 II

169. 多数元素（简单）

思路及代码： 169.多数元素

470. 用 Rand7() 实现 Rand10()（中等）

思路及代码： 470. 用 Rand7() 实现 Rand10()

202. 快乐数（简单）

思路及代码： 202. 快乐数