一、简述
这里讨论的算法主要是指应用于基于相机拍摄的显微镜的2D图像的拼接。基于2D显微图像的拼接通常只考虑x、y方向的位移。
图像拼接在图像处理中应用广泛。特别是对高分辨率标本成像的需求日益增加。通常,这些标本不适合显微镜的视野。为了克服这一缺点,使用移动样品的电动载物台来创建整个样品的平铺扫描。显微镜载物台提供的物理坐标不够精确,无法从单个图像堆栈重建(“拼接”)整个图像。
图像拼接的图像配准环节的技术路线通常分两种,第一种是基于输入图像中检测并提取关键点进行匹配等。另外一种是基于傅里叶移位定理一次计算两个图像之间所有可能的平移,在互相关度量方面产生最佳重叠。
相位相关(phase correlate)可以用于检测两幅内容相同的图像之间的相对位移量。可用于对齐图像,不具备光照不变性。它是基于傅立叶变换的位移定理:一个平移过的函数的傅立叶变换仅仅是未平移函数的傅立叶变换与一个具有线性相位的指数因子的乘积,即空间域中的平移会造成频域中频谱的相移。它的公式定义为:设二维函数(图像)f(x,y)的傅立叶变换为F(u,v),即DFT[f(x,y)]=F(u,v),如果f(x,y)平移(a,b),则平移后的傅立叶变换为:
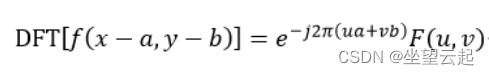
因此,当两幅函数f1(x,y)和f2(x,y)仅仅有位移的差异,即f2(x,y)= f1(x-a,y-b),则它们的傅立叶变换F1(u,v)和F2(u,v)有如下关系:

![Java并发体系-锁与同步-[2]](https://img-blog.csdnimg.cn/f373aef2e0a34d07be88c1b9c1b239c9.png)