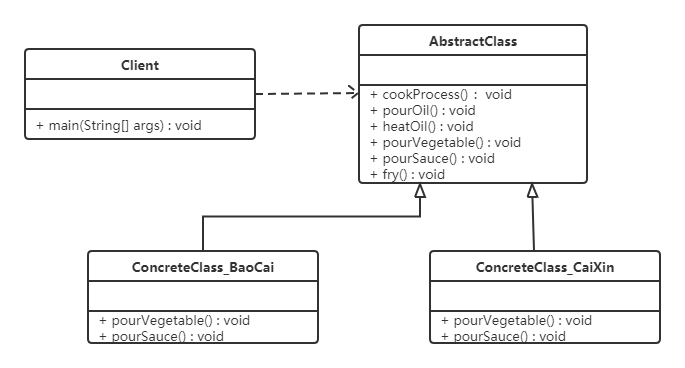
✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器
信号处理 图像处理 路径规划 元胞自动机 无人机 电力系统
⛄ 内容介绍
基于时间序列预测Arima模型和回归模型,以"职业需求总人数"为因变量,"人才缺口度""各类教育背景下的人数"和"就业岗位平均值"为自变量建立回归模型,并通过对自变量进行Arima时序预测,带入回归模型得到未来三年沈阳市潜在的人才需求,最后分析得:沈阳市对高技术人才比较看重,且人才缺口大,需要相应的政策来进行调整与补充.
⛄完整代码
clear;
close all
clc
P = sin(0.1:0.1:9.6);
F = sin(0.1:0.1:9);
%----------------------由于时间序列有不平稳趋势,进行两次差分运算,消除趋势性----------------------%
for i=2:96
Yt(i)=P(i)-P(i-1);
end
for i=3:96
L(i)=Yt(i)-Yt(i-1);
end
L=L(3:96);
Y=L(1:88);
%画图
figure;
plot(P);
title('原数据序列图');
hold on;
plot(Y,'r');
title('两次差分后的序列图和原数对比图');
%--------------------------------------对数据标准化处理----------------------------------------------%
%处理的算法 : (data - 期望)/方差
Ux=sum(Y)/88 % 求序列均值
yt=Y-Ux;
b=0;
for i=1:88
b=yt(i)^2/88+b;
end
v=sqrt(b) % 求序列方差
Y=yt/v; % 标准化处理公式
f=F(1:88);
t=1:88;
%画图
figure;
plot(t,f,t,Y,'r')
title('原始数据和标准化处理后对比图');
xlabel('时间t'),ylabel('油价y');
legend('原始数据 F ','标准化后数据Y ');
%--------------------------------------对数据标准化处理----------------------------------------------%
%------------------------检验预处理后的数据是否符合AR建模要求,计算自相关和偏相关系数---------------%
%---------------------------------------计算自相关系数-----------------------------------%
R0=0;
for i=1:88
R0=Y(i)^2/88+R0; %标准化处理后的数据的方差
end
for k=1:20
%R 协方差
R(k)=0;
for i=k+1:88
R(k)=Y(i)*Y(i-k)/88+R(k);
end
end
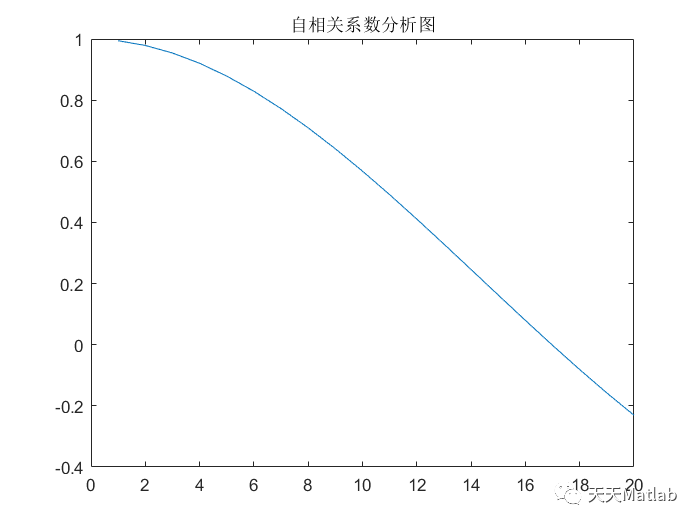
x=R/R0 %自相关系数x = 协方差/方差
%画图
figure;
plot(x)
title('自相关系数分析图');
%-----------------------------------计算自相关系数-------------------------------------%
%-----------------------解Y-W方程,其系数矩阵是Toeplitz矩阵(多普里兹矩阵)。求得偏相关函数X-------------------
X1=x(1);
X11=x(1);
B=[x(1) x(2)]';
x2=[1 x(1)];
A=toeplitz(x2);
X2=A\B %x=a\b是方程a*x =b的解
X22=X2(2)
B=[x(1) x(2) x(3)]';
x3=[1 x(1) x(2)];
A=toeplitz(x3);
X3=A\B
X33=X3(3)
B=[x(1) x(2) x(3) x(4)]';
x4=[1 x(1) x(2) x(3)];
A=toeplitz(x4);
X4=A\B
X44=X4(4)
B=[x(1) x(2) x(3) x(4) x(5)]';
x5=[1 x(1) x(2) x(3) x(4)];
A=toeplitz(x5);
X5=A\B
X55=X5(5)
B=[x(1) x(2) x(3) x(4) x(5) x(6)]';
x6=[1 x(1) x(2) x(3) x(4) x(5)];
A=toeplitz(x6);
X6=A\B
X66=X6(6)
B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7)]';
x7=[1 x(1) x(2) x(3) x(4) x(5) x(6)];
A=toeplitz(x7);
X7=A\B
X77=X7(7)
B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8)]';
x8=[1 x(1) x(2) x(3) x(4) x(5) x(6) x(7)];
A=toeplitz(x8);
X8=A\B
X88=X8(8)
B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9)]';
x9=[1 x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8)];
A=toeplitz(x9);
X9=A\B
X99=X9(9)
B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10)]';
x10=[1 x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9)];
A=toeplitz(x10);
X10=A\B
X1010=X10(10)
B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10) x(11)]';
x11=[1 x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10)];
A=toeplitz(x11);
X101=A\B
X1111=X101(11)
B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10) x(11) x(12)]';
x12=[1 x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10) x(11)];
A=toeplitz(x12);
X12=A\B
X1212=X12(12)
X=[X11 X22 X33 X44 X55 X66 X77 X88 X99 X1010 X1111 X1212]
%-----------------------------------解Y-W方程,得偏相关函数X-------------------------------------%
figure;
plot(X);
title('偏相关函数图');
%-----根据偏相关函数截尾性,初判模型阶次为5。用最小二乘法估计参数,计算10阶以内的模型残差方差和AIC值,应用AIC准则为模型定阶------%
S=[R0 R(1) R(2) R(3) R(4)];
G=toeplitz(S);
%inv(G)返回G的反函数
W=inv(G)*[R(1:5)]' % 参数W(i) 与X5相同 G*W = [R(1:5)]'
K=0;
for t=6:88
r=0;
for i=1:5
r=W(i)*Y(t-i)+r;
end
at= Y(t)-r;
K=(at)^2+K;
end
U(5)=K/(88-5) % 5阶模型残差方差 0.4420
K=0;T=X1;
for t=2:88
at=Y(t)-T(1)*Y(t-1);
K=(at)^2+K;
end
U(1)=K/(89-1) % 1阶模型残差方差0.6954
K=0;T=X2;
for t=3:88
r=0;
for i=1:2
r=T(i)*Y(t-i)+r;
end
at= Y(t)-r;
K=(at)^2+K;
end
U(2)=K/(88-2) % 2阶模型残差方差 0.6264
K=0;T=X3;
for t=4:88
r=0;
for i=1:3
r=T(i)*Y(t-i)+r;
end
at= Y(t)-r;
K=(at)^2+K;
end
U(3)=K/(88-3) % 3阶模型残差方差 0.5327
K=0;T=X4;
for t=5:88
r=0;
for i=1:4
r=T(i)*Y(t-i)+r;
end
at= Y(t)-r;
K=(at)^2+K;
end
U(4)=K/(88-4) % 4阶模型残差方差 0.4751
K=0;T=X6;
for t=7:88
r=0;
for i=1:6
r=T(i)*Y(t-i)+r;
end
at= Y(t)-r;
K=(at)^2+K;
end
U(6)=K/(88-6) % 6阶模型残差方差 0.4365
K=0;T=X7;
for t=8:88
r=0;
for i=1:7
r=T(i)*Y(t-i)+r;
end
at= Y(t)-r;
K=(at)^2+K;
end
U(7)=K/(88-7) % 7阶模型残差方差 0.4331
K=0;T=X8;
for t=9:88
r=0;
for i=1:8
r=T(i)*Y(t-i)+r;
end
at= Y(t)-r;
K=(at)^2+K;
end
U(8)=K/(88-8) % 8阶模型残差方差0.4310
K=0;T=X9;
for t=10:88
r=0;
for i=1:9
r=T(i)*Y(t-i)+r;
end
at= Y(t)-r;
K=(at)^2+K;
end
U(9)=K/(88-9) %9阶模型残差方差 0.4297
K=0;T=X10;
for t=11:88
r=0;
for i=1:10
r=T(i)*Y(t-i)+r;
end
at= Y(t)-r;
K=(at)^2+K;
end
U(10)=K/(88-10) % 10阶模型残差方差 0.4317
U=10*U
for i=1:10
AIC2(i)=88*log(U(i))+2*(i) % AIC值分别为:172.6632 165.4660 153.2087 145.1442 140.7898 141.6824 142.9944 144.5601 146.3067 148.7036
end
%-----------------取使AIC值为最小值的阶次,判断模型阶次为5。用最小二乘法估计参数--------------------%
%------------------检验{at}是否为白噪声。求{at}的自相关系数,看其是否趋近于零-----------------------%
C=0;K=0;
for t=7:88
at=Y(t)-W(1)*Y(t-1)-W(2)*Y(t-2)-W(3)*Y(t-3)-W(4)*Y(t-4)-W(5)*Y(t-5)+Y(6)-W(1)*Y(5)-W(2)*Y(4)-W(3)*Y(3)-W(4)*Y(2)-W(5)*Y(1);
at1=Y(t-1)-W(1)*Y(t-2)-W(2)*Y(t-3)-W(3)*Y(t-4)-W(4)*Y(t-5)-W(5)*Y(t-6);
C=at*at1+C;
K=(at)^2+K;
end
p=C/K %若p接近于零,则{at}可看作是白噪声
%--------------------------------{at}的自相关系数,趋近于零,模型适用--------------------------------%
%------------AR(5)模型方程为------------------------------------------------------------------------%
% X(t)=W(1)*X(t-1)-W(2)*X(t-2)-W(3)*X(t-3)-W(4)*X(t-4)-W(5)*X(t-5)+at (at=0.4420)
%------------------------------------------后六年的数据 进行预测和效果检验----------------------------------------------%
%-----------------------------单步预测 预测当前时刻后的六个数据----------------------------------%
XT=[L(84:94)];
for t=6:11
m(t)=0;
for i=1:5
m(t)=W(i)*XT(t-i)+m(t);
end
end
m=m(6:11);
%-------------预测值进行反处理---------------%
m(1)=Yt(90)+m(1); %一次反差分
z1(1)=P(90)+m(1); %二次反差分
m(2)=Yt(91)+m(2);
z1(2)=P(91)+m(2);
m(3)=Yt(92)+m(3);
z1(3)=P(92)+m(3);
m(4)=Yt(93)+m(4);
z1(4)=P(93)+m(4);
m(5)=Yt(94)+m(5);
z1(5)=P(94)+m(5);
m(6)=Yt(95)+m(6);
z1(6)=P(95)+m(6);
z1 % 单步预测的向后6个预测值:z1= 13.9423 13.4101 13.3588 12.9856 13.2594 12.9552
%---------------------------绘制数据模型逼近曲线-----------------------------------%
for t=6:88
r=0;
for i=1:5
r=W(i)*Y(t-i)+r;
end
at= Y(t)-r;
end
figure;
for t=6:88
y(t)=0;
for i=1:5
y(t)=W(i)*Y(t-i)+y(t);
end
y(t)=y(t)+at;
y(t)=Yt(t+1)-y(t);
y(t)=P(t+1)-y(t);
end
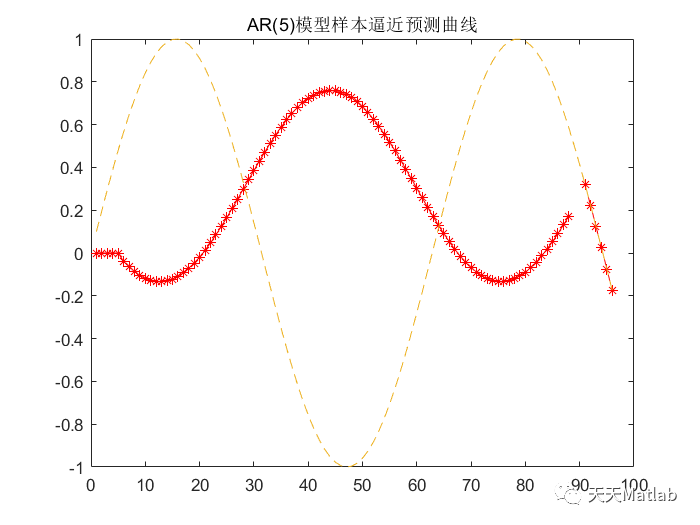
plot(y,'r-*'); % 样本数据模型逼近曲线
hold on;
plot(91:96,z1,'r-*');
hold on;
plot(P,'--'); % 原样本曲线
title('AR(5)模型样本逼近预测曲线');
%-----------------------------绘制数据模型逼近曲线-----------------------------------%
%-------------------------预测误差分析------------------------%
%----------------------------------多步预测 目的是向前六步预测--------------------------------------%
Xt=[ Y(84) Y(85) Y(86) Y(87) Y(88)]; %取当前时刻之前的6个数据
Z(1)=W(1)*Xt(5)+W(2)*Xt(4)+W(3)*Xt(3)-W(4)*Xt(2)-W(5)*Xt(1)
%------求向前l步的预测值
%预测步数小于5时
for l=2:5
K(l)=0;
for i=1:l-1
K(l)=W(i)*Z(l-i)+K(l);
end
G(l)=0;
for j=l:5
G(l)=W(j)*Xt(5+l-j)+G(l);
end
Z(l)=K(l)+G(l);
end
%预测步数大于5时(向前6步预测)
for l=6:6
K(l)=0;
for i=1:5
K(l)=W(i)*Z(l-i)+K(l);
end
Z(l)=K(l);
end
%----预测值进行反标准化处理
r=Z*v+Ux % 0.0581 0.0844 0.0156 0.0319 0.0632 0.0652
r(1)=Yt(90)+r(1); %一次反差分
z(1)=P(90)+r(1) %二次反差分
for i=2:6
r(i)=r(i-1)+r(i);
z(i)=z(i-1)+r(i)
end
%---------------------------- 预测误差分析 ------------------------------%
%-------计算绝对误差和相对误差
%D=[13.70 13.66 13.27 13.56 13.14 14.19 ]; % 预测值 z =14.0281 13.9606 13.9087 13.8887 13.9318 14.0403
D = sin(9.1:0.1:9.6);
for i=1:6
e6(i)=D(i)-z(i);
PE6(i)= (e6(i)/D(i))*100;
end
e6 % 多步预测的绝对误差 e = -0.3281 -0.3006 -0.6387 -0.3287 -0.7918 0.1497
PE6 % 多步预测的相对误差
1-abs(PE6) % 准确率
%------多步预测平均绝对误差
mae6=sum(abs(e6)) /6
%------多步预测平均绝对百分比误差
MAPE6=sum(abs(PE6))/6
%------绘制预测结果和实际值的比较图
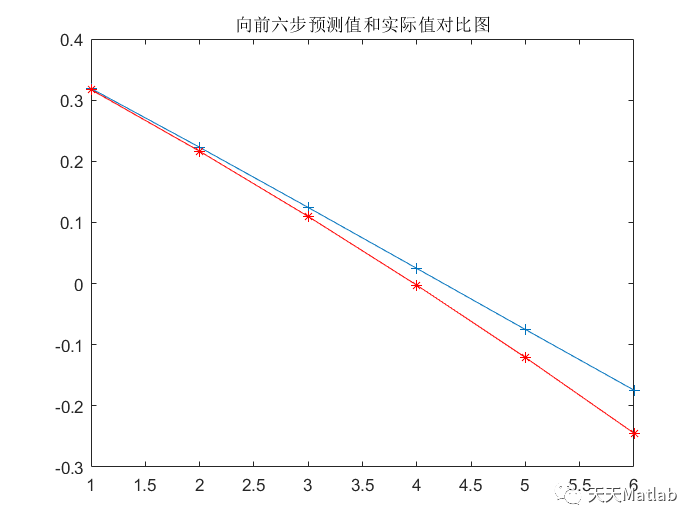
figure;
plot(1:6,D,'-+')
hold on;
plot(z,'r-*');
title('向前六步预测值和实际值对比图');
hold off;
function [yhat , se ] = arimapred(y,phi,theta,d,mu,sa2,l)
% ARIMAPRED(Y,PHI,THETA,D,MU,SA2,L) Forecast ARIMA process
% INPUTS:
% y = observed data; n by 1
% phi = vector of AR coefficients; p by 1
% theta = vector of MA coefficients; q by 1
% d = order of differencing; 1 by 1 integer
% mu = mean of d times differenced y process; 1 by 1
% sa2 = variance of "shocks"; 1 by 1 and positive
% l = forecast lead time; 1 by 1 positive integer
% OUTPUTS:
% yhat = point forecasts; l by 1
% se = prediction standard deviations; 1 by 1
[n m ] = size(y);
z = y;
if d > 0
for k = 1:d
z = z(2:(n-k+1)) - z(1:(n-k));
end
end
acvf = armaacvf(phi,theta,n-d+l);
V = toeplitz(acvf);
V11 = V(1:(n-d),1:(n-d));
V21 = V((n-d+1):(n-d+l),1:(n-d));
V22 = V((n-d+1):(n-d+l),(n-d+1):(n-d+l));
mu1 = mu*ones(n-d,1);
mu2 = mu*ones(l,1);
[ zhat Vp ] = blip(z,mu1,mu2,V11,V22,V21);
if d==0
yhat = zhat;
se = sqrt(diag(Vp));
else
A = tril(ones(l,l));
B = A^d;
Vpy = B*Vp*B';
se = sqrt(diag(Vpy));
dy = [ y(n-d+1) ];
if d > 1
yend = y((n-d+1):n);
for k = 2:d
yend = diff(yend);
dy = [ dy ; yend(1) ];
end
end
yhat = zhat;
for k=1:d
yhat = cumsum([ dy(d-k+1) ; yhat ]);
end
yhat = yhat((d+1):(l+d));
end
⛄ 运行结果
⛄ 参考文献
[1]张斌, 安连新, 孙凯. 基于ARIMA时间序列预测的人才需求变动研究[J]. 经营者, 2019.
⛄ Matlab代码关注
❤️部分理论引用网络文献,若有侵权联系博主删除
❤️ 关注我领取海量matlab电子书和数学建模资料
![[附源码]计算机毕业设计springboot校园快递柜存取件系统](https://img-blog.csdnimg.cn/a9db337c85ae4d49b3ce70a868dd0052.png)