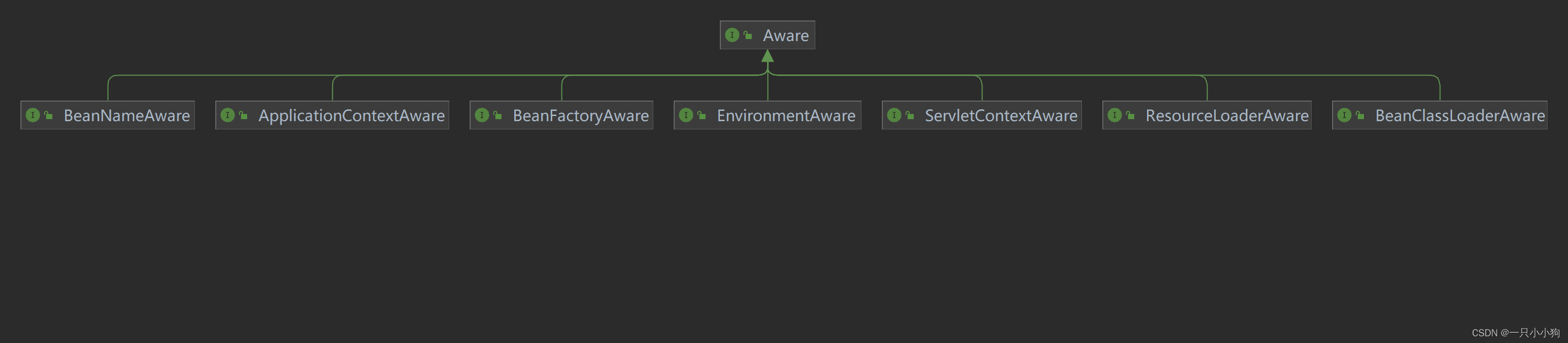
在前面的章节里,我们谈到了积分环节由于执行器的物理限制导致的积分项Wind-up,通过设置饱和限幅器,选择性关闭积分环节来完成Wind-up问题。
今天我们要解决的问题就是微分环节可能存在的问题。通过传感器我们可以观测出一个被控量的大小,和前面说到的anti-windup一样,受到物理环境的限制,对于传感器而言,那就是噪声。
我们知道微分环节其实就是对误差的一个求导,几何意义就是斜率,斜率越大,表示控制系统受到的影响也越大。如果噪声变化量很大(或者说频率很大)系统将会受到很大的影响。
测量导致的噪声
传感器是会受到周围环境的干扰,它反映的通常不是实际值。比如:
- Thermal noise
- Shot noise
- Flicker noise
- Brust noise
- Coupled noise
- White noise
我们感兴趣的是他们是如何影响我们的系统的。虽然对于某些控制规律中,只要噪声是一个低幅度的,他可以看成是对系统无关紧要的影响,但对这次要讲的理想PID而言是不一定的。

上图,黄色的斜线代表了高低频率噪声的斜率,斜率越大,对微分项影响也越大,从而会影响我们整个控制的输出。或者你可以从代数角度来解释,因为所有信号都可以看成是无穷个正弦信号的组合:
n
o
i
s
e
=
y
(
t
)
=
A
sin
(
ω
a
t
+
ϕ
a
)
+
B
sin
(
ω
b
t
+
ϕ
b
)
+
⋯
noise=y(t)=A\sin(\omega_at +\phi_a)+B\sin(\omega_b t+\phi_b)+\cdots
noise=y(t)=Asin(ωat+ϕa)+Bsin(ωbt+ϕb)+⋯
为了简化问题,我们只考虑第一项:
y
(
t
)
=
A
sin
(
ω
a
+
ϕ
a
)
y(t)=A\sin(\omega_a +\phi_a)
y(t)=Asin(ωa+ϕa)
其中,
A
A
A表示幅值,
ω
a
\omega_a
ωa角频率,
ϕ
\phi
ϕ相角。
对其进行求导:
y
(
t
)
=
A
⋅
ω
a
⋅
sin
(
ω
a
+
ϕ
a
+
9
0
∘
)
y(t)=A\cdot\omega_a\cdot\sin(\omega_a+\phi_a+90^{\circ})
y(t)=A⋅ωa⋅sin(ωa+ϕa+90∘)
只看幅值部分,有以下结论:
- 当 ω a > 1 r a d / s \omega_a> 1rad/s ωa>1rad/s 幅值变大
- 当 ω a < 1 r a d / s \omega_a<1rad/s ωa<1rad/s 幅值变小
可以画出以下图形:

随着角频率的增大,幅值也增大;反之,角频率越小,幅值也越小。我们想要的是设定一个合理的截断,降低其对微分项的影响。重新回到我们的PID图:

理想情况我们希望将所有噪声都分离出来,事实上不可能做到。索性的是,大多数噪声高幅值的通常具有较低频率,高频率的往往具有较低幅值。显然使用一个低通滤波器是合适的,比如说一阶低通滤波器。

设定一个截止频率,小于这个频率的都保留,大于这个频率的都过滤。这样的处理将会使得噪声对于我们的系统影响降低。
拉普拉斯变换
| 拉普拉斯域的传递函数 | 含义 |
|---|---|
| S | 微分 |
| 1/S | 积分 |
| N/(S+N) | 截止频率为N rad/s低通滤波器 |
考虑一个低通滤波器:
10
S
+
10
\frac{10}{S+10}
S+1010
常数项10就是代表截止频率为
10
r
a
d
/
s
10 rad/s
10rad/s的一阶低通滤波器。不过我们也会写成其他形式:
N
S
+
N
=
1
1
N
S
+
1
=
1
τ
S
+
1
\frac{N}{S+N}=\frac{1}{\frac{1}{N}S+1}=\frac{1}{\tau S+1}
S+NN=N1S+11=τS+11
因为频率的倒数是时间,所以这个
τ
\tau
τ也被称为时间常数。
OK!

这里再提一下,如果实现等价方法(积分反馈回路):

那么我们如何在这两种方法中选择呢?第一种方法逻辑清晰易懂,但是实现起来效率不高,第二种则是抽象,但是效率较高。
来看看matlab中simulink是如何使用的:
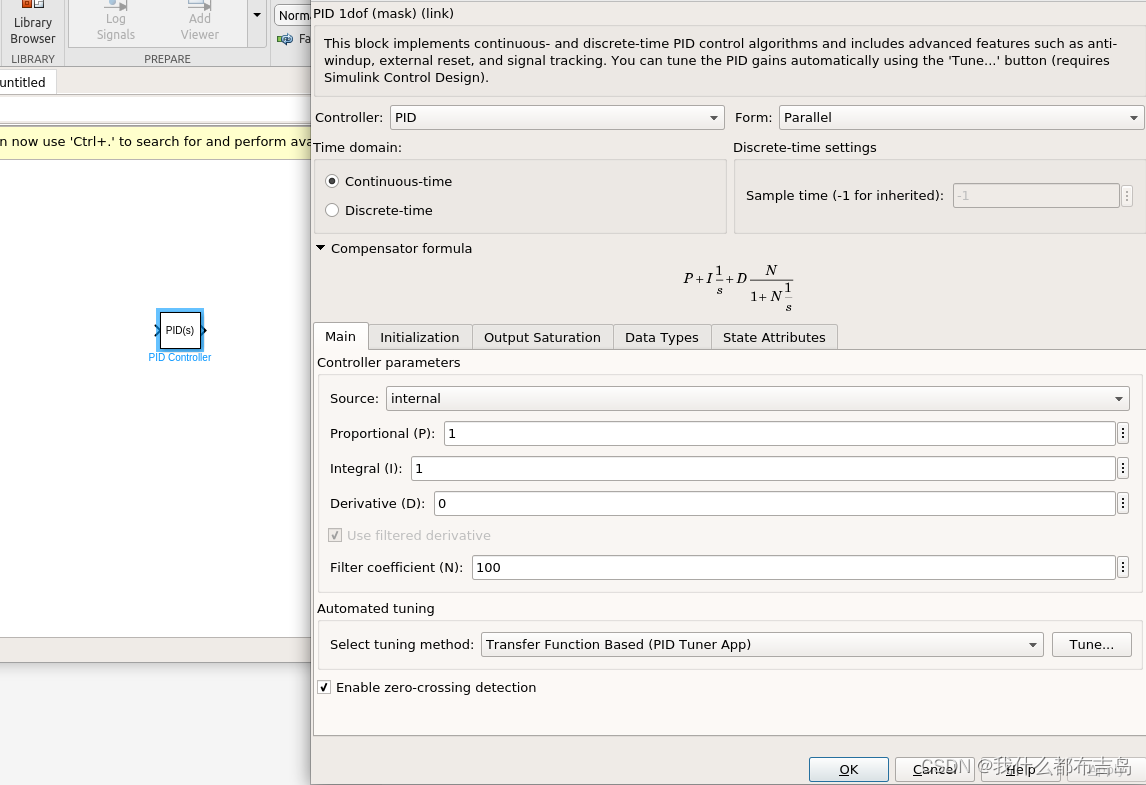
可以看出,Simulink中的微分项是:
D
N
1
+
N
1
s
D\frac{N}{1+N\frac{1}{s}}
D1+Ns1N
显然他不是一纯粹的微分环节,他是带了低通滤波,截止频率为
N
N
N.