Roses are red, violets are blue,
both are somehow similar, but the classifier has no clue.
论文题目:《SimLoss: Class Similarities in Cross Entropy》(2020年)
论文地址:https://arxiv.org/pdf/2003.03182v1.pdf
1.背景
神经网络分类任务中一种常见的损失函数是分类交叉熵(CCE),它平等地惩罚所有错误分类。但是,类通常具有固有的结构。例如,将玫瑰的图像分类为“紫罗兰”比分类为“卡车”要好。为此提出SimLoss,它是 CCE 的直接替代品,它结合了类相似性以及两种从特定任务构建此类矩阵的技术。在年龄估计和图像分类任务上实验,发现SimLoss在几个指标上的表现优于CCE。总结为一句话来讲就是:Simloss是能够考虑到类之间相关性的图像分类损失函数。
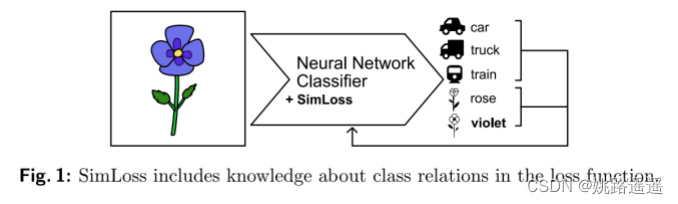
2.SimLoss

SimLoss和交叉熵损失最主要的区别就是上述公式()里面的内容。对于SimLoss来说,()里的内容表示每个类别的概率输出分别乘以该类别与标签类别的相似度,然后加和。因此相比于交叉熵损失平等的惩罚所有错误分类,Simloss不仅考虑到了对正例的惩罚,也兼顾了对不同负例的惩罚或者叫容忍度。
3. 相似度矩阵S的创建
两种分类任务相似度矩阵S的创建:Class Order & General Class Similarity
3.1. Class Order

我后续在年龄估计上进行的实验就是利用的这种矩阵创建方式,因为对于年龄估计来说它的类别之间有固定的顺序,例如,婴儿和儿童之间相邻,距离就为1,婴儿和青少年中间隔了个儿童,那么他们的距离就为2。体现在公式上就是|i-j|,因为r是属于0到1之间的,那么矩阵S的所有值也就是相似度取值范围都是在0到1之间的。
举个具体的例子,假设现在我们年龄分类的类别标签一共有8个:婴儿、儿童、青少年、青年、青中年、中年、中老年和老年,现有一张图像的标签为青少年,那么它与其他7个类别(包括自身)的距离可以设置为2、1、0、1、2、3、4、5,假设超参数r取值为0.3,那么我们就可以得到婴儿类别与其他类别(包括自身)的相似度向量:[0.09, 0.3, 1, 0.3, 0,09, 0.0.27, 0.0081, 0.00243],类似的,我们就可以得到每个标签与其他标签(包括自身)的相似度向量,所有的向量组合起来就形成了我们的相似度矩阵S,如下:
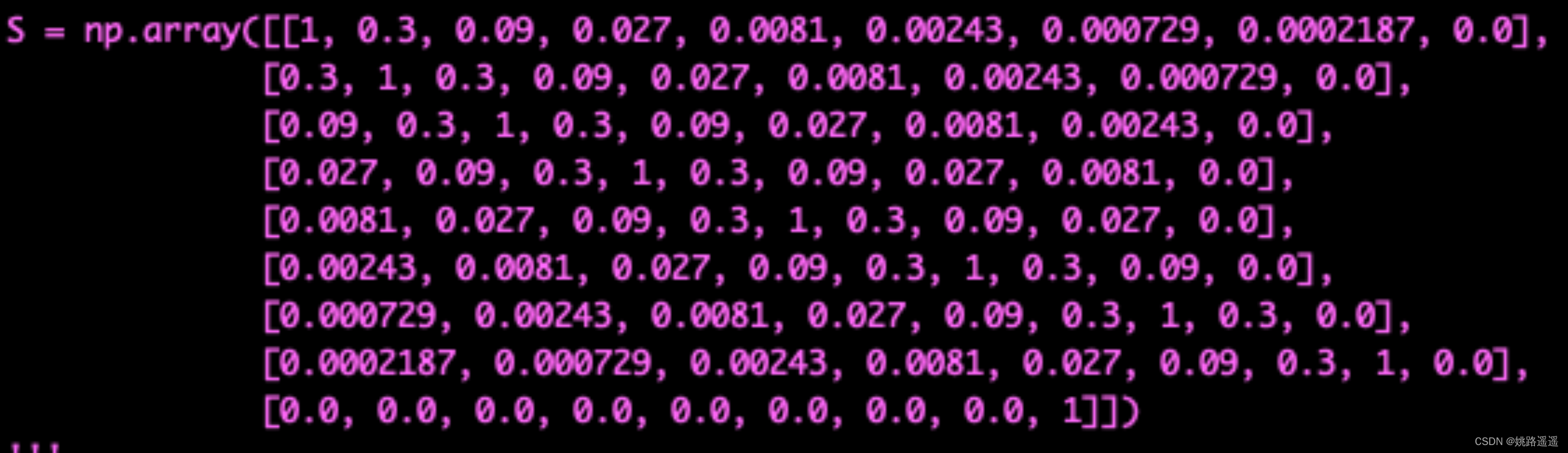
假设现在一张图片的标签为青年,它的模型得分为[0.02, 0.03, 0.04, 0.77, 0.05, 0.04, 0.03, 0.02],对于交叉熵损失来说,onehot形式为[0, 0, 0, 1, 0, 0, 0, 0],对应的损失为-log(0.77)。那么对于SimLoss来说,我们可以根据上面预先设定好的相似度矩阵得到青年与其他类别标签(包括自身)的相似度,即为:[0.027, 0.09, 0.3, 1, 0.3, 0.09, 0.027, 0.0081],根据第2节提到的SimLoss公式,可以得到损失为:-log(0.02x0.027+0.03x0.09+0.04x0.3+1x0.77+0.05x0.3+0.04x0.09+0.03x0.027+0.02x0.0081)。对比交叉熵损失与SimLoss,我们可以很清晰的看出,SimLoss提高了对于与标签类别相似度高的标签的容忍度。(极端情况下,如果超参数r设置为1的话,那么相似度矩阵S里的值都为1,也就意味着没有损失了)
3.2. General Class Similarity

公式中的sim(i,j)就是你所定义的类别i和j之间的相似度,可以是手动的、半自动的或全自动的去设置。l它的作用就是作为一个下界,体现在公式上就是,如果两个类别之间的相似度小于l直接取0。
4. 试验结果
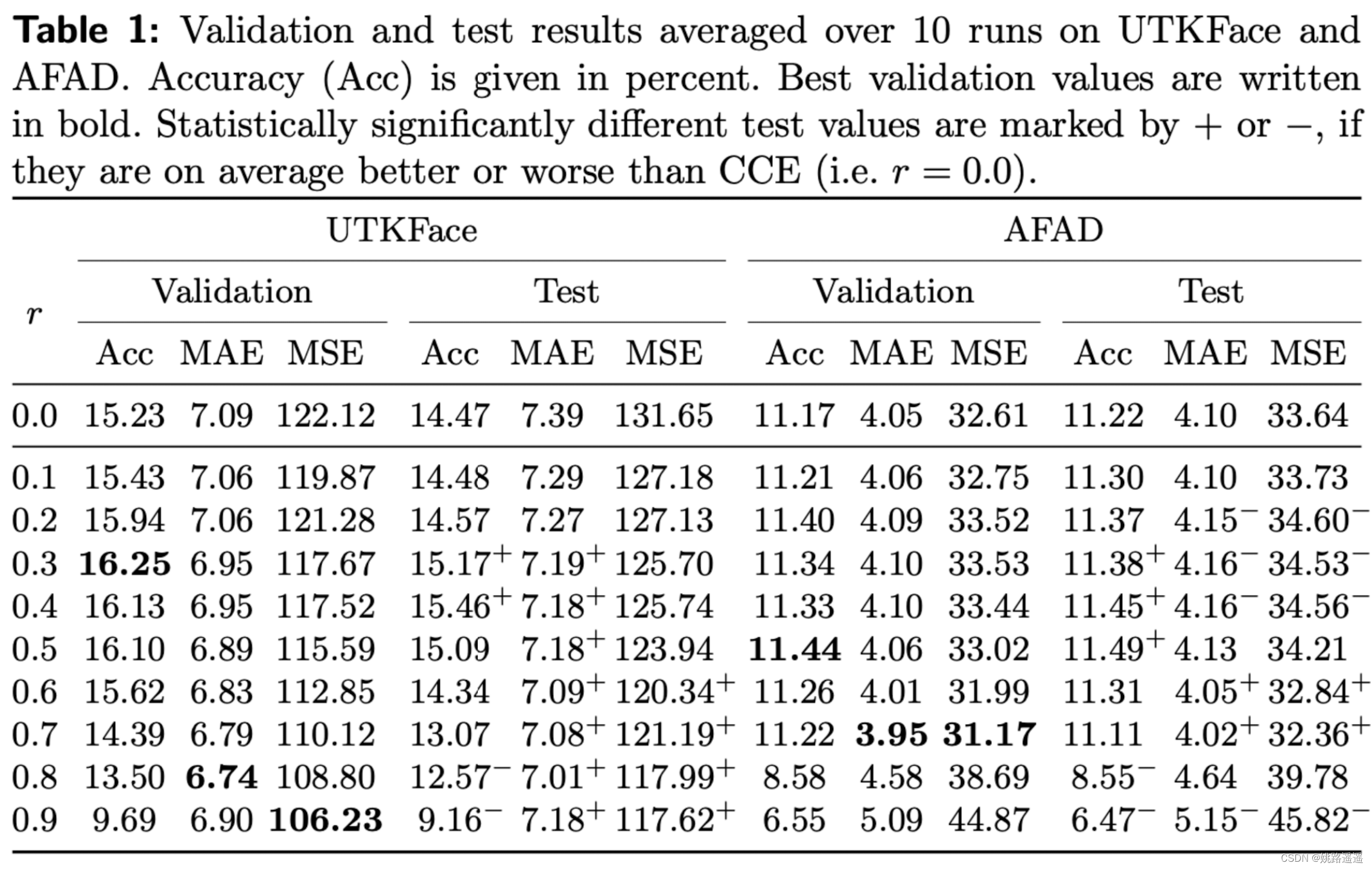
表1 是在两个年龄估计数据集上对于不同的的缩减因子 r 的的平均指标。r=0就是代表交叉熵损失,可以看到验证集和测试集上表现最好的缩减因子总是高于 0.0,这意味着 SimLoss 优于 CCE。对于 UTKFace,0.3 的缩减因子取得最佳验证Acc,而 0.8 或 0.9 分别取得最优的 MAE 和 MSE。对于 AFAD,r = 0.5 验证Acc最高,而 r = 0.7 MAE 和 MSE最优。总体而言,选择较小的缩减因子 r ≈ 0.4 可优化准确率,而较大的 r ≈ 0.8 可优化 MAE 和 MSE。这是因为较大的 r 会导致更高的矩阵值,也就是相似度,因此对于估计接近正确年龄的类别的惩罚会更小。
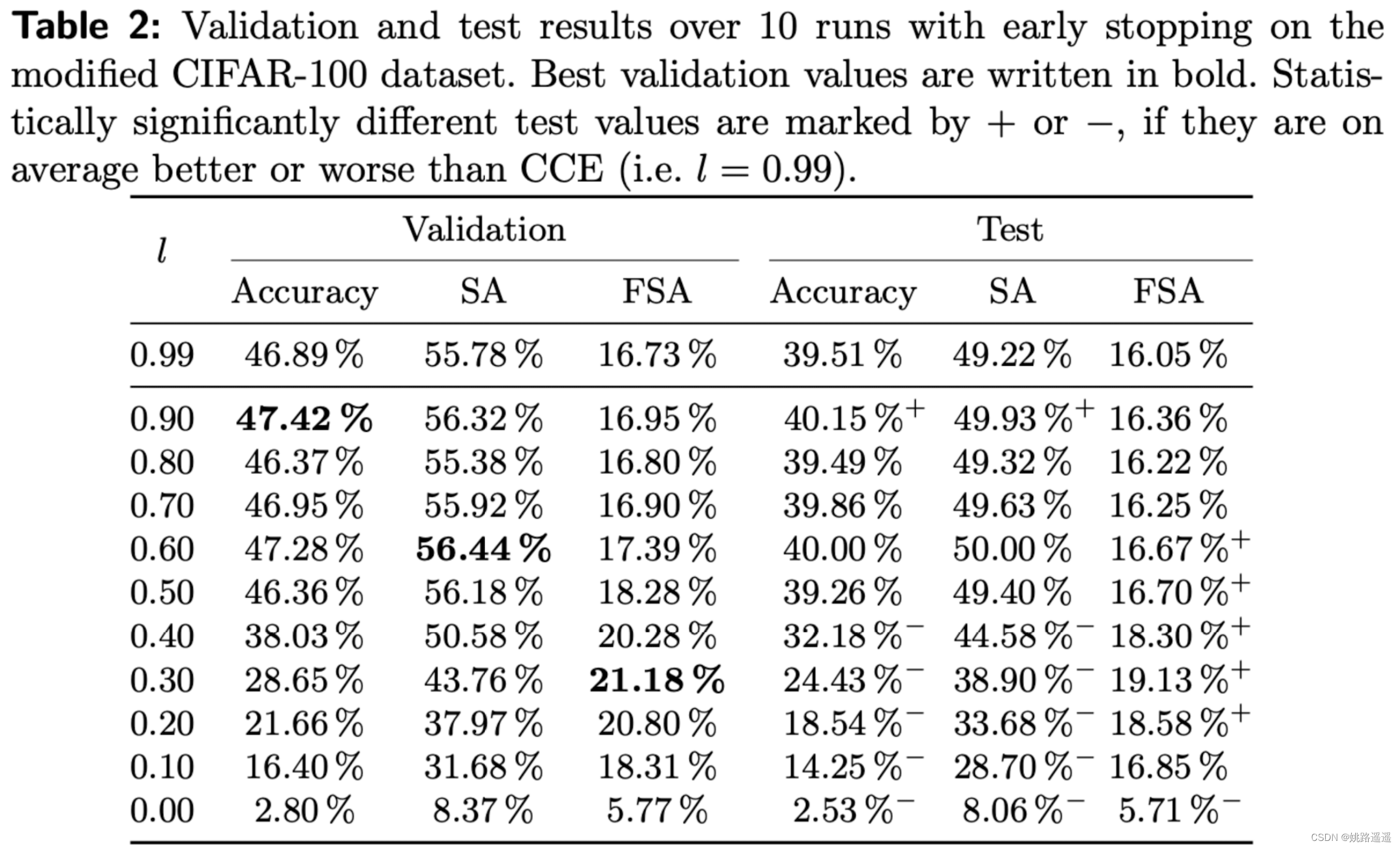
对于图像分类任务,表 2 显示了给定下界 l 的 CIFAR-100 数据集的验证和测试集的结果,对于 l ≈ 1,损失相当于 CCE,平均而言,表现最好的模型的下限总是小于 0.99,l = 0.9时取得最佳acc ,较小的下限往往会降低准确性,因为损失函数几乎不会惩罚任何错误分类。







![[附源码]计算机毕业设计springboot小型银行管理系统](https://img-blog.csdnimg.cn/2276d17ac8374f3f9b8e4daa06228f32.png)