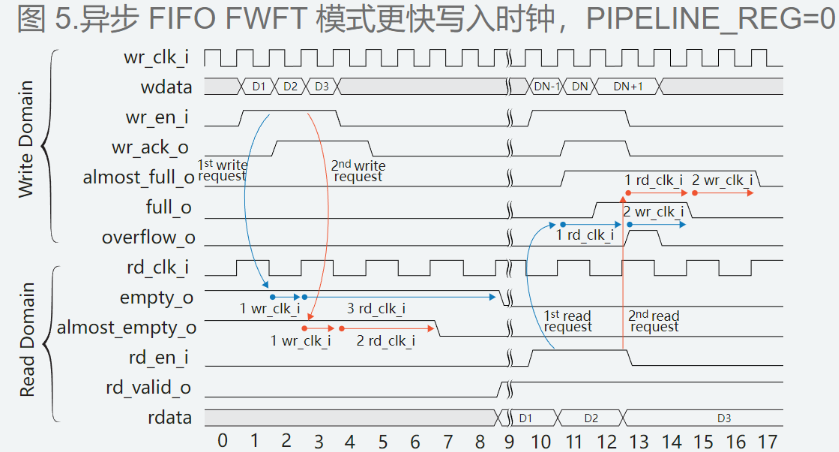
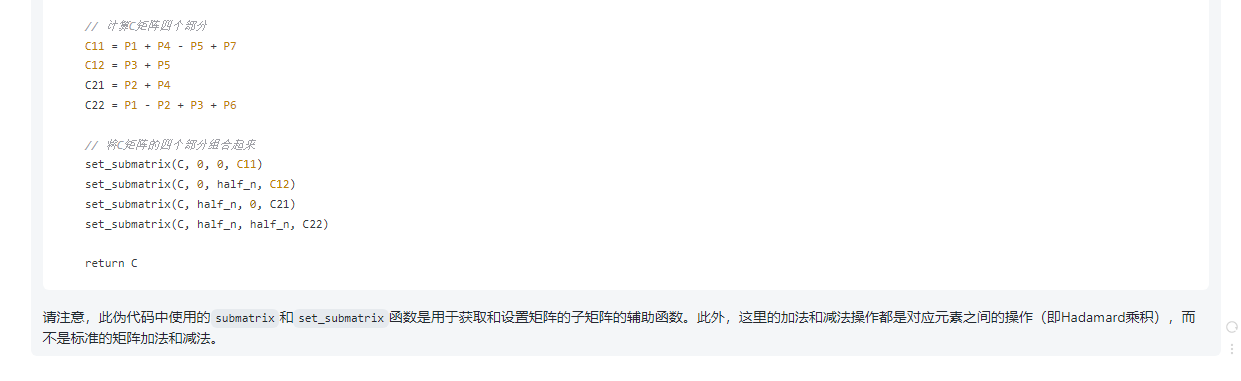
顺序查找概念:从表的另一端开始,一次将记录的关键字和给定值进行比较,若某个记录的关键字和给定的值相等,则查找成功,反之则查找失败。
ASL:平均查找长度
pi查找概率,ci查找次数

eg:序列1,2,3
查找1的次数为1概率为1/3,2为两次概率1/3,3的次数为3概率1/3
将123的查找率*查找次数的结果累加得到 平均查找次数

顺序查找的代码实现:(这里我么用的顺序表查找)
//顺序查找
typedef struct List
{
int* data;//数据元素
int* length;//数据长度
int size;//有效数据个数
}List;
List* initList(int length)
{
List* list = (List*)malloc(sizeof(List));
list->length = length;
list->data = (int*)malloc(sizeof(int) * length);
list->size = 1;//size等于1的时候说明带有哨兵,后面的数据从第二个位置开始存元素。
return list;
}
void listAdd(List* list,int data)
{
if (list->size == list->length)//所存储的有效数据已经等于空间大小(空间已经满了)
{//这里我们重新定义一个newlength,防止开始length为0时,length*2=0;
int newlength = list->length == 0 ? 4 : list->length * 2;
int* tmp = (List*)realloc(list->data, newlength * sizeof(int));
if (tmp == NULL)
{
printf("空间开辟失败\n");
exit(-1);
}
else
{
list->data[list->size] = data;
list->size++;
}
}
else
{
list->data[list->size] = data;
list->size++;
}
}
void printlist(List* list)
{
for ( int i = 0; i <list->size ; i++)
{
printf("%d ->", list->data[i]);
}
printf("NULL\n");
}
int search(List* list, int key)
{
int i=0;
list->data[0] = key;
//for循环后面没有语句只有分号时,当不满足for循环的条件后循环结束不再进行,直接进行下一语句。
for (i = (list->size) - 1; list->data[i] != key; i--);//for循环后面没有语句的执行的时候需要添加分号,防止后面的语句直接进入for循环中。
return i;//如果返回的为0则认为没有查找到,因为我们把要查找的元素放在了头节点当中。
}
int main()
{
List* list = initList(5);
listAdd(list, 1);
listAdd(list, 2);
listAdd(list, 3);
listAdd(list, 4);
listAdd(list, 5);
printlist(list);
printf("%d\n", search(list, 3));
return 0;
}顺序查找的ASL:第一个节点需要1次,第n个节点则需要n次
则总该查找的次数为Sn=n*(n+1)/2(等差数列求和公式)
每次查找的概率为1/n
所以顺序查找的ASL为:n*(n+1)/2*(1/n)=(n+1)/2
所以时间复杂度为O(n)。
二分查找L(折半查找):
前提条件是有序序列,即每次从序列的中间开始于所要查找的元素比较,如果中间元素小于key(要查找的元素)则从中间元素的右边查找(以中间元素+1为首元素,尾元素不变,再去求mid于key相比)。同理若key<mid则要从mid的左边寻找(以中间元素-1为尾元素,首元素素不变,在去求mid于key比较),若key等于mid则返回。
代码实现:利用循环查找
//循环查找
int binarysearch(int key,List* list)
{
int start = 0;
int end = list->size - 1;
int mid = 0;
while (start<=end)/如果我们的首元素下标大于尾元素下标则说明我们已经遍历完整个序列不存在要找的元素
{
mid = (start + end) / 2;
if (list->data[mid] < key)
{
start = mid + 1;
}
else if (list->data[mid]>key)
{
end = mid - 1;
}
else
{
return mid;
}
}
return -1;//-1表示不存在
}
递归实现二分查找:
//递归查找 1.分半2查找(左查/右查)。
int binarysearchRecursion(int key, List* list, int start, int end)
{
//出口
if (start == end)//每个递归都有一个终止条件相当于我们while中的start<=end,当两个下标相等时进行判断如果等于key则返回任意一个下标,如果不相等则说明没有找到
{
if (list->data[start]==key)
{
return start;
}
else
{
return -1;
}
}
int mid = (start + end) / 2;
//每次查找不到进行递归,看key于mid的比较来判断如果缩小范围
if (list->data[mid] < key)
{
return binarysearchRecursion(key, list, mid+1, end);
}
else if (list->data[mid]>key)
{
return binarysearchRecursion(key, list, start, mid - 1);
}
else
{
return mid;
}
}二分查找的时间复杂度:(两个二分查找的世家复杂度相同所以我们只讲解一个即可)
我们可以把线性表堪称一颗树(因为线性表是有序的比key小的都在其坐标,比它大的都在其右边)
eg:

树的查找:节点在第几层需要查找几次,h层需要查找h次(所有的算法都符合此条件)
假设有n个节点,h层==》由树的公式得到n=2^(h-1) 一棵满二叉树。
满二叉树:每一层有2^(h-1)个节点
每一层查找次数:节点个数*层数==2^(h-1)*h
每层的ASL:查找次数 *概率=1/n*2^(h-1)*h
分解求2^(h-1)*h如何用n来代替
观察得此为等差*等比数列,求法(错位相减Sn-hSn)

3,4式联立:

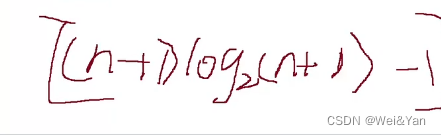
再去×1/n得到整个顺序的ASL

再利用我们数学极限n趋向足够大的时候前面的分式可以约掉,所以结果
约等于:两个都可
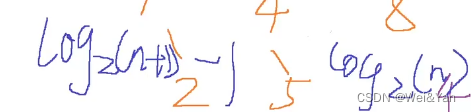
顺序查找于二分查找以简略的讲完,一些图片资料与代码都借鉴于b站upTyrantLucifer