杂的问题。从帕斯卡开始,机械计算机越做越精巧,内部结构越来越复杂,当然能够完成的功能也就越来越多。按照大家通常的思路,要想实现更复杂的功能,就需要设计和制造更复杂的机械,帕斯卡就是这么做的。但最终,机械(计算机)复杂到一定程度,就无法造出来了,巴贝奇本人最终成为这种想法的牺牲者。
布尔是和巴贝奇同时代的人。布尔虽然创办过一所中学,后来还在爱尔兰科克(Cork)郡的一所学院当教授,但是在他生前没有什么人认为他是数学家,而和主流科学界有着密切来往的巴贝奇也不知道他的工作,否则巴贝奇也许不会把差分机设计得那么复杂。布尔在工作之余,喜欢阅读数学论著,思考数学问题,并最终形成了他布尔代数的构想。1854 年,布尔的《思维规律的研究》(An Investigation of the Laws of Thought, On Which Are Founded the Mathematical Theories of Logic and Probabilities)一书出版,第一次向人们展示了如何用数学的方法解决逻辑问题。在此之前,人们普遍的认识是数学和逻辑是两个不同的学科,今天联合国教科文组织依然把它们严格区分开。
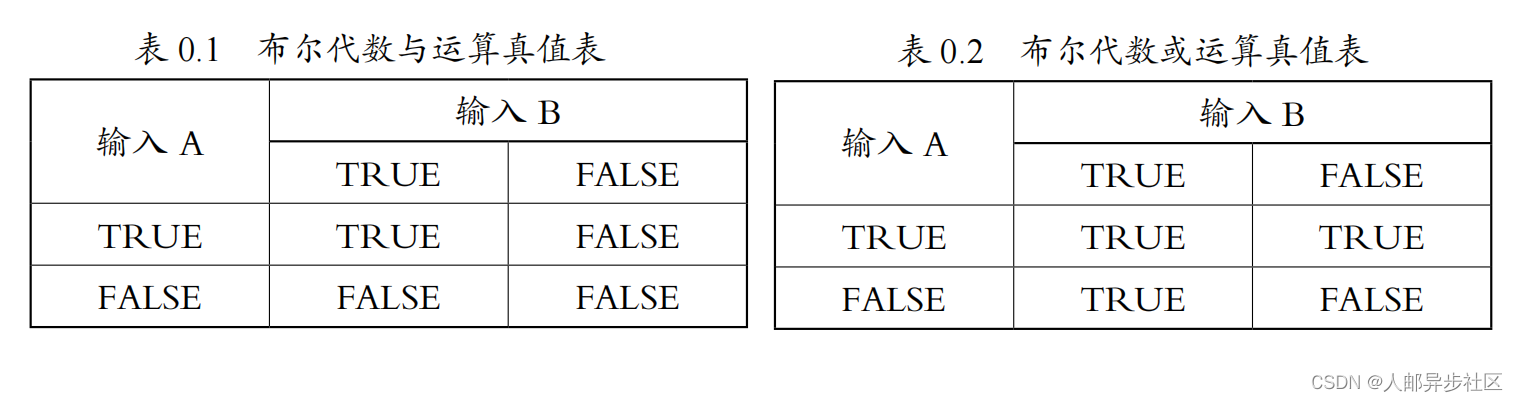
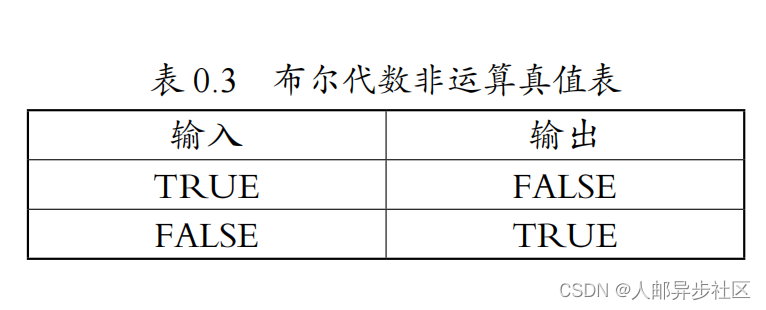
布尔代数简单得不能再简单了:运算的元素只有两个,即 1(TRUE,真)和 0(FALSE,假);基本的运算只有“与”(AND)、“或”(OR)和“非”(NOT)三种[这三种运算都可以由“与非”(AND-NOT)或者“或非”(OR-NOT)一种运算导出],这些运算只用表 0.1 ~表 0.3 所示的真值表就能完全描述清楚。
布尔在世的时候并不知道自己发明的这种代数有什么好的应用场景,但是在 80 年之后,当模拟计算机的发明人万尼瓦尔·布什(Vannevar Bush)(发明了微分分析仪,这是一种模拟计算机)将改进这种计算机的任务交给 22 岁的香农时,布尔代数一下子派上了大用场。
在电子计算机被发明之前,布什发明的微分分析仪是世界上计算能力最强大的计算机,如图 0.4 所示。但是这种计算机有两个问题:首先,它是靠机械装置实现计算的;其次,它是模拟的,精度提高的空间有限。因此,到了 20 世纪 30年代,它就难以再改进了,这种情景和当年巴贝奇难以改进机械计算机的情况很类似。

香农没有像巴贝奇那样,试图依靠设计更复杂的计算机来解决更复杂的计算问题,而是在看到分析仪走到死胡同时,退回到计算这个问题的本源,开始寻找用简单方法解决复杂问题的路径。香农发现世界上的很多现象和布尔代数的逻辑是对应的,比如电路的接通与断开、电压的高和低、数学上的 0 和
1
等。因此,他提出一个想法,用基于布尔代数的逻辑电路来控制分析仪的运转,这样可以让分析仪解决更复杂的问题。在此基础上,香农进一步发现,加、减、乘、除各种运算都是由很多个基本的逻辑电路“搭”出来的,就如同用乐高积木可以搭出一个复杂的房子一样。也就是
说,香农在布尔代数和算术运算之间搭起来一座桥梁,这座桥梁就是简单的逻辑电路。
1937
年香农完成硕士论文后,布什专门安排他到华盛顿去做了论文答辩,这篇题为《继电器和开关电路的符号分析》的论文第二年在电气电子工程师学会(IEEE
)的学报上发表了,它被誉为 20
世纪最重要的硕士论文
[1]
。就是这么一篇薄薄的,甚至略带稚气的论文,奠定了今天所有数字电路设计的基础,可谓是彪炳千秋。
香农的电路设计思想可以被总结为“模块化”和“等价性”。
所谓模块化就是用少量简单的模块搭建出各种复杂的功能,这是今天计算机行业的核心指导思想。比如,我们要设计一台功能非常强大的程控交换机,其中基本的模块是非常简单的。要设计一台超级计算机(即媒体上所说的“超算”),用大量相同的模块搭就可以了。很多学者讲,超算其实从计算机科学角度来看水平并不高,更多的是工程的成就,就是这个道理。
模块化的思想使得计算机产业和其他工业相比有很大的不同。一般的工业产品有大量形状和功能各不同的组成部分,比如一辆汽车里的上万个零件,形状各异,就连一台钢琴也有上千个不同的零件。但是在计算机产品中,常常是大量相同模块的复制,这就是 IT
产业能够发展很快、后来摩尔定律能够成立的重要原因。
当然,计算机和
IT
产品容易通过模块化实现的背后还有一个原因是等价性,即再复杂的计算都可以等价成很多加、减、乘、除的运算,再进而等价成开关电路的逻辑运算。也就是说,只要实现了后者,就可以间接地实现前者。在计算机科学中,我们常常会遇到这样一种情况:某个问题很难解决,不过存在一个容易解决的等价问题,于是我们会先解决那个等价问题,等到它被解决后,原来的问题也就迎刃而解了。这就好比在几何里,虽然两个三角形全等的定义是三条边和三个角都相等,但是我们不需要直接从这些方面证明,只需要证明两个角相等、另外有一条边相等即可,后者的难度要比原先定义中的难度低很多。在计算机科学上也是如此,计算机科学家常常要证明两件事情是等价的,而计算机工程师的工作则是要实现等价的桥梁。我们在后面会专门讲如何通过等价性来解决一个复杂的问题,并且如何找到等价关系。比如我们会讲到一个卡特兰(Catalan
,又译作卡塔兰)数的概念,然后会向大家展示很多看似不相关的问题都可以与之等价起来。
讲回早期计算机的发展历程,像巴贝奇那样直接实现微积分的计算是一件非常困难的事情。但如果把微积分计算变成加、减、乘、除运算,再变成更为简单的二进制逻辑运算,事情就变得容易多了。当然,把复杂的计算问题变为一系列二进制的运算,就是今天的软件工程师要做的事情了。当然,在 20 世纪早期,并没有什么专职的软件工程师,计算机的设计者需要自己解决这个问题。
有意思的是,世界上第一个用模块化原理实现可编程计算机的并不是香农,也不是他论文的读者,而是德国的力学工程师楚泽。作为精通力学的工程师,楚泽的数学功底非常深厚。他大学毕业时正值德国准备发动第二次世界大战,因此他到了一家飞机制造厂从事飞机的设计工作。这项工作涉及大量烦琐的计算,而当时的计算工具只有计算尺。很快楚泽就发现其实很多计算使用的公式是相同的,只是代入不同的数据而已,比如,计算飞机机翼的宽度从 10
米到
11
米每变化
1
厘米时飞机的升力。这种重复的工作完全应该交给机器去完成,而不是动用大量的专业人才。有了这个想法后,楚泽于 1936
年辞职回(到父母)家,开始研究这种能够计算的机器了。在此之前,楚泽对计算机一无所知。同年(指 1936
年),图灵博士已经提出了可计算性理论,香农正在写那篇改变世界的硕士论文,但由于楚泽并不属于科学家的圈子,因此直到第二次世界大战结束他都不知道图灵和香农等人的理论,楚泽甚至不知道一个世纪前的巴贝奇的工作。当时,楚泽只有 26
岁,完全是凭着一腔热情,加上良好的数学基础,独自一人在家研制能够计算的机器。所幸的是,由于有了几年从事工程计算的经验,楚泽深知能计算的机器不应该只服务于一种或者几种特定的计算,而是应该能做各种计算,至于怎么算,应该有一些指令序列来控制这种机器。更幸运的是,楚泽知道布尔代数,懂得用二进制来实现运算和控制机械计算机。当然他还需要实现十进制和二进制的转换,这也可以通过简单的机械模块来实现。至于为什么要多此一举进行十进制到二进制再到十进制的两次转换,其实很简单,因为 0
和
1
(或者开和关)这两个操作在机械上容易实现,而要用机械实现十进制的运算则很难。和香农等人所不同的是,楚泽不是理论家,完全是从一个工程师的经验出发发现了和香农开关电路类似的规律,遗憾的是他虽然做出了实物,却不能像香农一样提出一整套
理论。
楚泽最终采用简单方法实现了复杂的计算功能,他发明了人类第一台可编程的计算机 Z1,Z 是楚泽名字(Zuse)的首字母。
Z1
是一台机械计算机,由电动机提供动力,驱动一大堆齿轮组工作。如果你单纯数一数,会发现 Z1
中的零件个数并不比巴贝奇设计(而没有实现)的计算机的少,但是 Z1
里面的设计逻辑非常简单,只是简单模块的大量复制,因此楚泽才能以一已之力完成它。虽然 Z1
可以用程序控制,但是它并不能实现后来图灵机的全部功能,比如它不能比较两个数值的大小。此外,这台计算机是纯机械的,计算速度受限于机械运动,自然就很慢,每秒只能完成一次计算。
楚泽在成功地研制出
Z1
之后,得到了德国政府的资助,还有了助手,这让他的工作进展顺利了许多,很快他将计算机由机械的改成了继电器的,取名 Z2
,速度达到每秒五次计算。随后他又在计算机的逻辑控制上做了重大改进,研制出了第三个版本的 Z3
计算机。这台使用了
2000
多个继电器的计算机实际上实现了图灵机所描绘的功能,尽管楚泽当时依然不知道图灵的工作。
楚泽的成功有很大的偶然性,但在偶然性的背后也蕴藏着很多必然的因素。
首先,楚泽没有重复巴贝奇的失败经历,去研制一个非常复杂的计算机,他找到了一条解决复杂问题的正确道路,即先实现一种(或者几种)最基本的简单模块,然后大量复制那些简单模块实现各种复杂的功能。在 Z1
到
Z3
的具体设计过程中,楚泽巧妙地利用了等价性原则,通过实现二进制计算间接地实现了十进制运算。
今天一些媒体在报道量子计算时犯的一个共同的错误,就是认为量子计算的优势在于突破了二进制,因此可以让计算机完成现在不能够完成的事情。这显然是外行话,因为无论计算采用几进制,它们在数学上都是等价的,采用二进制办不到的事情,使用四进制、八进制或者十进制同样办不到。量子计算在解决特定问题时的确效率会很高,但这和是否采用二进制无关。
其次,楚泽生逢其时。人的命运通常受到大环境的影响,计算机在第二次世界大战前后在大西洋两岸都获得了突破性的进展,这是大环境使然。在巴贝奇的年代,计算机最大的用途是计算数学用表,而到了第二次世界大战前,武器设计和加密 / 解密中有大量的计算要用的计算机。这时政府对计算机的研究支持就变成大强度、持续性的了。我在《全球科技通史》中讲到,很多重大发明最后一步的完成,或者说临门一脚,要靠集中很高的能量密度才能实现。楚泽的时代正是那样一个时代。
不过由于楚泽的工作缺乏理论基础,是很难在此基础上将计算机科学快速推进的。自工业革命之后,各种发明能够不断涌现,一项技术能够不断改进,新版本的产品能够不断出现,都离不开理论的指导,在计算机领域也是如此。在第二次世界大战之前,在这个领域贡献最大的理论家当数图灵了,他从数学上奠定了可计算问题的理论基础,或者说他提出了计算机的数学模型—
图灵机。
要点
等价性、模块化,以及通过它们化繁为简。
思考题 0.2
利 用“ 与 非 ”(
AND-NOT
)运算实现 布 尔 代 数 中 的 与、 或、 非 三 种 运 算。(🌟🌟)
0.3 图灵机:计算的本质是机械运动
世界上有两种思维方式。其中一种是从生活的经验出发一点点地认识更大的世界,比如人认识数字的时候便是如此,从1
、
2
、
3
一直数到
100
。今天我们所说的“迭代式进步”“小步快跑”其实都是这种方式的别称而已。在科学史上,这种方式有一个更正式的名称,叫作“工匠式的进步”。在计算机发展的历史上,是需要这种工匠式进步的,比如摩尔定律所带来的进步其实就是工匠式的。虽然每 18
个月翻一番的速度看上去不算太惊人,但是持续 10
年就能得到
100
倍的进步。直到图灵之前,人类造计算机时也是按照这种方式做的:先从研制能解决简单问题的计算机开始,再越做越复杂。
不过,在历史上时不时地会出现思维超越时空的天才,比如牛顿和爱因斯坦。在计算机领域也有这样的人物,首推后来被誉为“计算机科学之父”的图灵。图灵博士
在真正了解计算机的人群中,被看成神一样的人。在 20
世纪,全世界智力上可以和爱因斯坦平起平坐的人恐怕只有图灵和冯·
诺依曼(
von Neumann
,又译作冯
·
诺伊曼) 两个人了(而后者被认为智力甚至超过了爱因斯坦)。“神人”自然有超越常人的地方, 图灵在思考和计算机相关的问题时,会回到这个问题的本原,抛开具体的技术,从计算的本质来寻找计算机的极限。
在
20
世纪
30
年代中期,图灵就开始思考下面三个非常根本的问题。
1
.数学问题是否都有明确的答案。
2
.如果有明确的答案,是否可以通过有限步的计算得到答案。
3
.对于那些有可能在有限步计算出来的数学问题,能否有一种假想的机器,它不断地运动,最后当它停下来的时候,那个数学问题就解决了。
这些问题在我们很多人看来更像是哲学家思考的问题,因此我们普通人是无法像图灵那样直奔主题的。当然“神人”也有导师,图灵也不例外。他的两个导师(其实是精神导师)一个是当时普林斯顿大学教授兼普林斯顿高等研究所所长冯 ·
诺依曼,另一个是更早一些的大数学家希尔伯特(Hilbert
)。图灵当时是普林斯顿大学的学生,虽然冯 ·
诺依曼并非他的论文导师,但是对他的影响很大。图灵在读了冯
·
诺依曼的《量子力学的数学基础》一书后很受启发,他认为人的意识基于不确定性原理,但是计算则基于机械的运动(电子的运动可以被认为是等价于机械运动)。今天我们知道,前者代表不确定性,后者代表确定性,它们都是这个世界固有的特性。图灵很懂得在边界里做事情,他把注意力放到了解决那些能够通过机械运动解决的问题,即可计算的问题上。
那么什么问题是可计算的?图灵从著名数学家希尔伯特那里得到了启发。
希尔伯特是一位了不起的数学家。今天人们了解希尔伯特,通常是因为他的名字和 23 个著名的数学问题(即所谓的希尔伯特问题)联系在一起,但他对数学的贡献远不止于此。希尔伯特一方面像他的前辈勒内·笛卡儿(René Descartes)、艾萨克·牛顿(Isaac Newton)和奥尤斯丁·柯西(Augustin Cauchy)以及他的后辈安德烈·柯尔莫哥洛夫(Andrey Kolmogorov)那样构建出完整的数学分支 [1] ;另一方面从最根本之处出发,将数学作为一个整体思考。希尔伯特一直在思考这样三个问题。
1
.数学是完备的(
complete
)吗?所谓完备性,就是说对于任意一个命题,要么可以证明它是对的,要么可以证明它是错的。
2
.数学是一致的(
consistent
)吗?所谓一致性,就是说一个命题不能既是真的,又是假的。
3
.数学是可判定的(
decisive
)吗?所谓可判定性,就是说一个具体的问题,你能否判断它是否有答案。
希尔伯特的这三个问题从本质上划定了数学的边界。因为数学只能解决那些在数学上是完备的问题,而数学的一致性则能保证它没有似是而非的答案。当然,对于这三个问题,希尔伯特自己也不知道答案,不过他希望数学既是完备的,也是一致的。后来著名数学家哥德尔解决了前两个问题,他指出数学不可能既是完备的,又是一致的,这就是数学中著名的哥德尔不完全性定理。哥德尔的理论告诉我们,世界上有很多问题我们无法判定它们的对错,因此它们不是数学问题。对于第三个问题,希尔伯特引申出一个具体的问题,也就是希尔伯特第十问题(简称第十问题)。第十问题是这样说的:对于任意多个未知数的整系数不定方程,要求给出一个可行的算法 [2]
,使得借助于它,通过有限次运算,可以判定该方程有无整数解。
为了更好地理解这个问题,我们不妨看三个例子。
1
.
x
2
+
y
2
=
z
这个方程显然有整数解,它们就是勾股数。
2
.
x
3
+
y
3
=
z
3
这其实就是费马大定理的一个特例,这个问题在困惑了人类几百年后,由安德鲁·
怀尔斯 (
Andrew Wiles
)最后证明它无解。这个问题和上一个问题不论是有解还是无解,都是可判定的。
3
.
3
x
3
+2
x
2
+
y
3
=
z
3
它有没有整数解呢?对于这个方程是否成立,希尔伯特也不清楚,因此他把问题提出来.1970
年,苏联杰出的数学家尤里
·
马季亚谢维奇(
Yuri Matiyasevich
)证明,对于这个方程,以及绝大多数不定方程,我们既不能证明它们有整数解,也无法证明解不存在。
我们对比希尔伯特的三个疑问和图灵的三个疑问就可以看出:前者关心的是一个问题是否是数学问题,如果是,能否判定它有答案;而后者关心的则是,如果已经判定它是数学问题,能否在有限的步骤内通过机械的方法找到答案。特别要说的是,第十问题就是图灵前两个疑问的特例,如果对第十问题的答案是否定的,就等于图灵前两个疑问的答案也是否定的。当然,图灵不可能在 1936
年就知道第十问题的答案,因此他也不清楚自己的前两个问题的答案是什么,但他隐隐约约地感觉到答案应该是否定的,即很多数学问题没有明确的答案,即使有也无法在有限步内找到。于是,图灵将精力集中在那些能够在有限步内计算出来的数学问题上。为此,他设计了一种后来被称为图灵机的数学模型,这个模型的全部定义一共只有四条,用通俗的语言讲就是这样的。
1
.要有一条(无限长的)被分成一个个格子的纸带,每个格子里记录着符号或数字。为了清楚起见,可以为这些格子编上号:1
、
2
、
3
……这就相当于人们计算数学题时使用的纸张。
2
.有一个读写头(可以想象成铅笔),在纸带上左右移动,它停在哪里就可以改变哪里的符号或者数字,这就相当于人们算题时写写画画的过程。
3
.有一套规则表,根据图灵机当前的状态和读写头所指格子中的符号或数字,人们查表后就能知道下一步该做什么。当然完成这步操作后,图灵机也就进入了新的状态。这张表就相当于老师教的算题方法,或者珠算口诀。图 0.5 显示了图灵机中状态改变的过程。
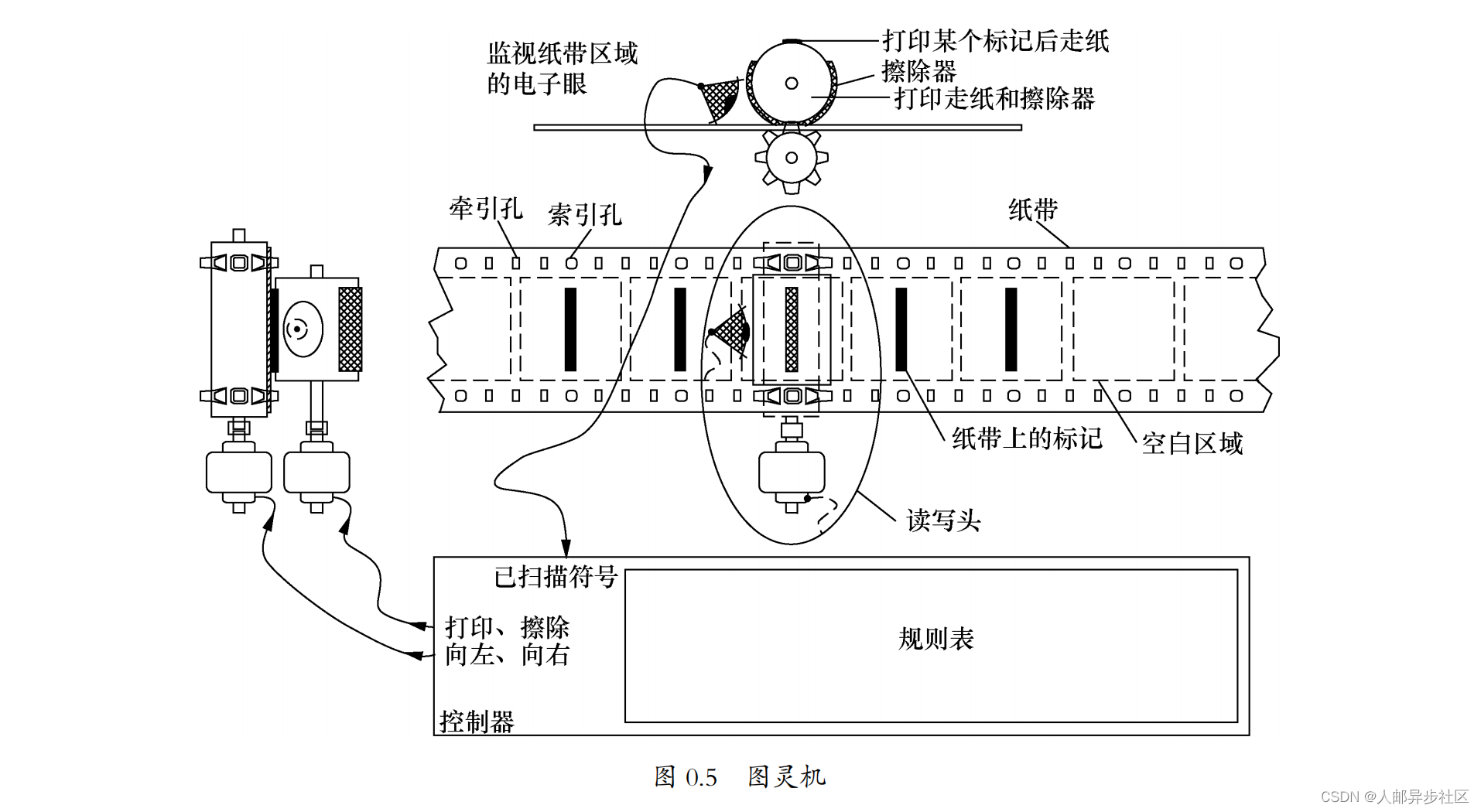
4
.当然,图灵机的状态需要记录在一个地方,即寄存器(里面的内容就相当于我们算题时的中间结果)。图灵机的状态数量是有限的,其中有一个特殊的状态是停机,一旦进入这个状态则表示计算完成。
图灵认为这种机器能模拟任何具体计算的过程,但并未指出如何实现这样一台计算机。图灵机的意义至少有这样三个。
首先,它将世界上的数学问题分为两类:一类是可以用上述机器在有限步内完成计算的,当然这个“有限”可以非常长;另一类是不可以的。今天我们在计算机科学中说一个问题可不可以计算,不是指在数学上能否计算,而是指能否用图灵机这样一个简单的逻辑来计算。从这中间可以看出来,能用图灵机计算的问题,其实只是可计算数学问题的一小部分。
其次,图灵机虽然是虚构的,但是它给后人设计计算机制定了一个行之有效的原则,特别是图灵提出了存储地址、计算机状态、规则表(即今天我们说的指令集)和当前位置读写头这四个重要概念。今天我们应用的真实的计算机,依然建立在这些概念的基础之上。
最后,图灵机求解数学问题的过程和机械运动对应起来了。今天的电子计算机可以被理解成由很多能够被控制的开关构成,这些开关的运动和计算过程是对应的。也就是说,今天计算机计算的本质其实就是机械运动。
图灵是超越时代的人,他不是跟在别人后面来观察一件事情发展的规律,而是在前面等着大家,告诉大家什么问题能解决、什么不能,然后对那些可以解决的问题给出一个大方向。至于有了方向之后该怎么办,就是大家要考虑的问题了。1946
年出现的电子计算机 ENIAC
(
Electronic Numerical Integrator and Computer
,直译为电子数字积分计算机)其实就是一种实用的图灵机。
要点
图灵机、可计算的问题。
思考题 0.3
如果计算的本质是机械运动,那么信息处理和能量就存在一个对应关系。比如,我们可以计算一下 1946
年的
ENIAC
消耗
1
度电(
1
千瓦时)能完成多少次计算,今天的华为 P30
手机消耗
1
度电能完成多少次计算。( 🌟🌟)
0.4 人工智能的极限
2016
年,当
Google
的
AlphaGo
战胜李世石之后,很多人就开始担心世界上所有的事情是不是计算机都能做得比人好。这种担心多少有点杞人忧天,因为无论是什么样的计算机,只能解决世界上的很小一部分问题。
我们在前面讲到,世界上的很多问题都不是数学问题,这一点希尔伯特和库尔特·
哥德尔(
Kurt Gödel
)等人已经证实了。因此,如果我们画一个大圈代表所有问题(假定是集合 S
1
)的话,那么所有的数学问题(集合
S
2
)只是这个大圈中的一个小圈而已。
在数学领域,只有一部分问题我们能够判断是否存在答案,大部分问题是无法判断答案是否存在的。
1970
年马季亚谢维奇最终解决了第十问题,对人类来讲,不知道这算是一个福音,还是一个诅咒。从积极的方面来讲,人类又解决了一个难题,而且把数学的边界,特别是可计算的边界划得更准确了。从消极的方面讲,就连形式简单的不定方程我们都无法判定答案存在与否,更不要说那些复杂的数学问题了。如果那么多的数学问题我们无法知道是否存在答案,那就更不可能用逻辑的方法推导出答案了。因此,我们可以将数学问题中的一小部分看成可判定(是否有答案)的问题(集合 S
3
),而真正有答案的问题(集合 S
4
)的数量则更少,如图
0.6
所示
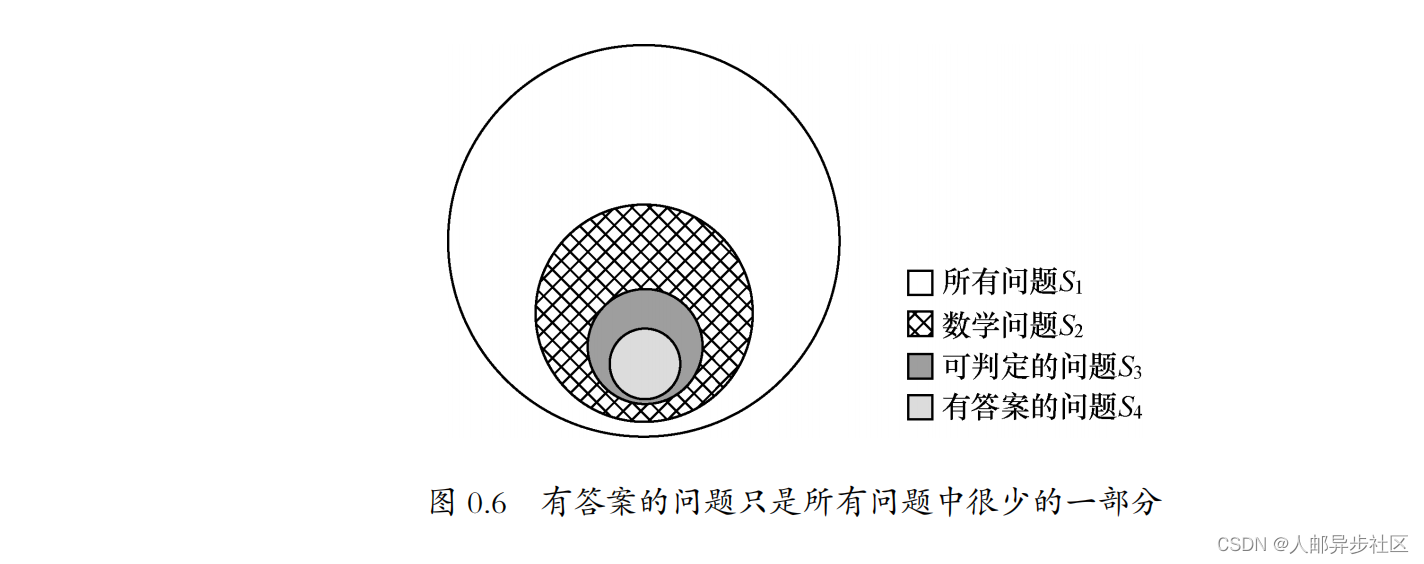
在有答案的问题中,有一些是可以通过图灵机解决的问题(集合 S5),就是我们在前面说到的可计算问题。当然,图灵机是一种理想状态的计算机,它所谓的有限时间可以非常长,比如一万亿年,超过宇宙的年龄,因此现实生活中的计算机能解决的问题(即工程可解问题,集合S 6)是可计算问题的一个小的子集。比如说那些计算复杂度等于或者超过指数函数的问题,都属于在工程上无法解决的问题。有人会问:计算机再快一万倍怎么样?一万倍也没有用,因为计算机多算不了几步,就把这一万倍的提升给耗尽了。2018 年,Google 宣布在量子计算上获得了突破,可将一些密码的破解速度提升上亿倍。从表面上看,似乎我们使用的加密方法今后会变得不安全,但是,即使计算机的计算能力提升了,只要我们把密码的长度加长一倍,计算机破解它的计算量可能就需要增加万亿倍。
对于这种从理论上讲有解,但是计算时间特别长的问题,如果能够有近似的方法将其变成多项式复杂度的问题,比如我在《数学之美》中介绍的条件随机场 (Conditional Random Field)的问题,那么就被认为在工程上是有解的,否则它们在工 程上依然无解。
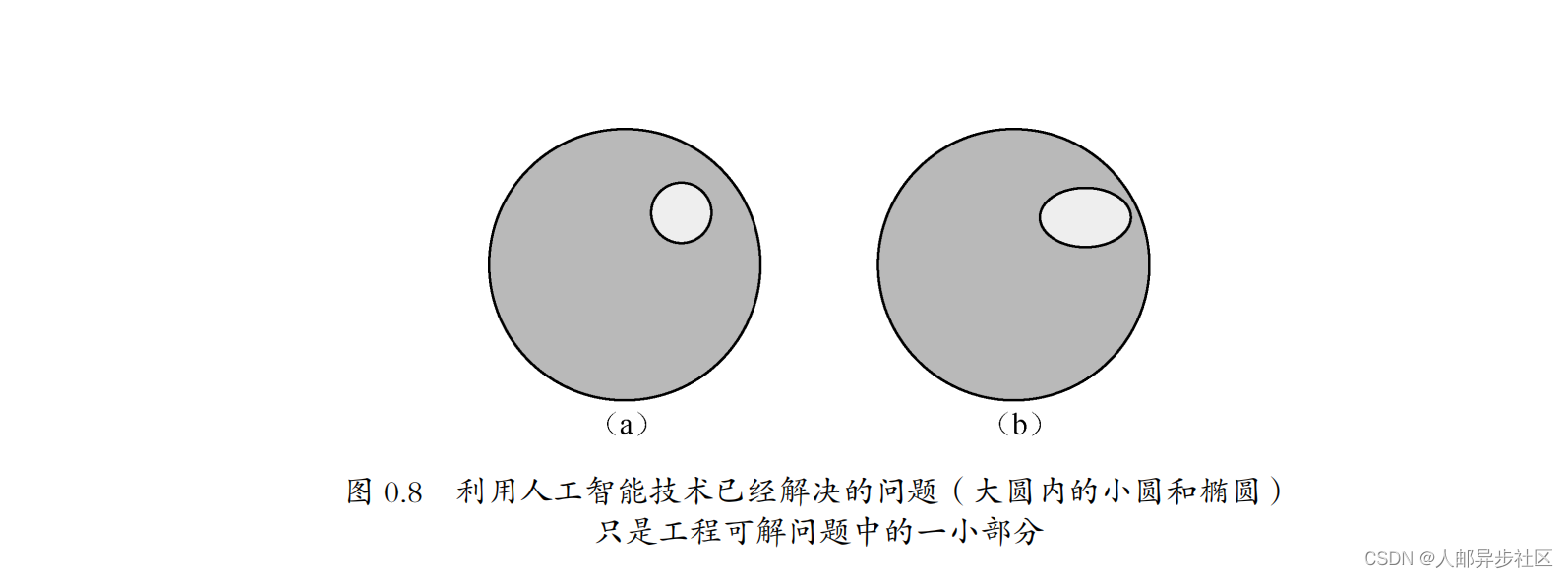
今天的人工智能主要是指基于大数据的深度学习。我们可以把一个人工智能 系统理解为由特定程序(控制指令序列)控制的、能够解决某一类问题的计算机。 这一类问题,比如语音和图像识别、无人驾驶、计算机自动翻译、下围棋或者象棋等,我们通常称之为人工智能可解问题,并没有超出图灵机可计算问题的范畴。 事实上,它们只是工程可解问题的一个子集 S7
,如图 0.7 所示。
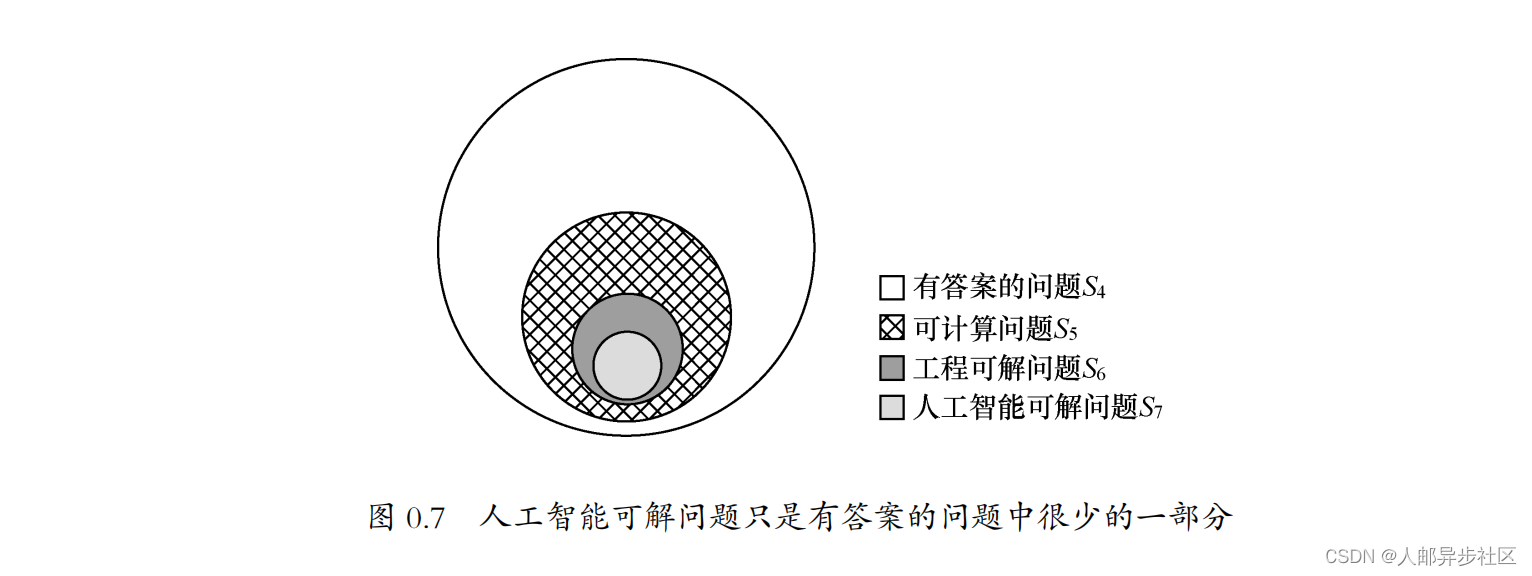
人工智能的计算机之所以显得很聪明,能做越来越多的事情,只是因为很多问题过去大家没有找到转变为数学问题的桥梁,现在找到了而已。也就是说集合
S
7
沿着某个维度扩大了一些范畴,如图
0.8
所示。但是无论怎么扩展,它都不可能超出可计算这个范畴。
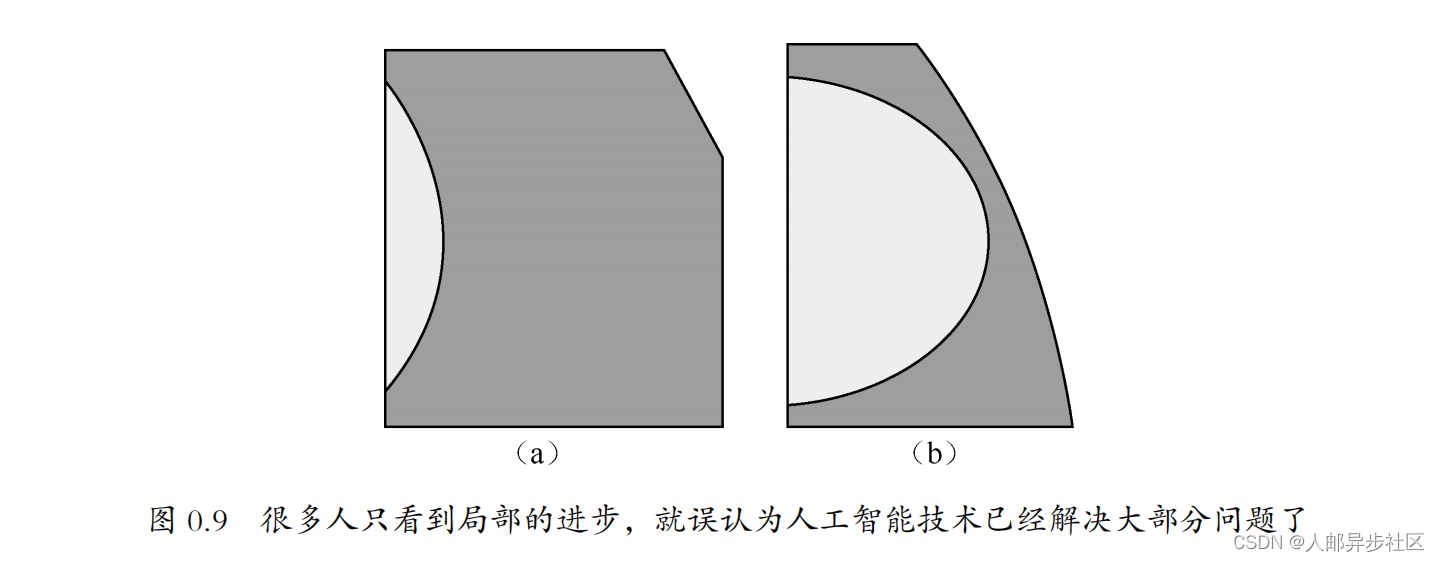
今天,很多计算机领域的从业者(特别是做出了一些具体贡献的人)会从自己的角度出发放大这种作用,因为在很多人眼里,人工智能所解决的问题放大的范围已经占到了工程可解问题,乃至所有问题的很大一部分(图中浅色部分),如图 0.9
所示。
迄今为止,计算机相关理论和技术的发展都没有超越图灵机的范畴。也就是说80 多年前图灵为计算机所能解决的问题划的那条线,至今还没有被逾越。这也说明理论对工程的影响有多么深远。为什么在学术界,大家急于试着越过图灵画的红线呢?这其实没有必要。
今天,世界上需要用计算机、用人工智能来解决的问题实在太多,因此将注意力放在利用它们解决现有的问题上,而不是杞人忧天,或者异想天开,更有意义。未来是否会有能够解决非数学问题的机器?或许会有,但不是我们今天所谈论的计算机。
要点
人工智能的边界。
思考题 0.4
在数字计算机出现之前曾经出现过模拟计算机,如何证明后者等价于前者的某个
子集?( 🌟🌟🌟)
结束语
一台计算机应该包括计算、存储和控制三个部分。人们通常注意到的其实是前两部分,忽视的是控制部分。计算机从本质上来讲是在不断地做机械运动,能够进行什么样的计算、完成什么样的任务,就看人们如何控制计算机了。当然,我们今天不会像使用算盘那样一步一步地操控计算机,而是将所有的控制指令以程序的形式输入计算机中,这样计算机就在程序的控制下完成了人们想让它们做的事情。
在计算机早期的发展过程中,计算机的复杂程度和它能够解决的问题的复杂程度是同步增加的。但是当问题越来越复杂之后,就无法制造出更复杂的计算机了,也就是说用复杂办法解决复杂问题的思路走不通了。于是香农和楚泽等人改变了思路,用简单的方法解决复杂的问题,具体讲,就是使用开关电路实现各种计算,而开关电路的基础是布尔代数。香农和楚泽解决复杂问题的方法论,依然是今天我们学习计算机科学理论和使用计算机时必须牢记的最根本的原则。
在这个世界上,并非所有的问题都是数学问题,即便是数学问题,也并非都可以通过计算机来解决。图灵的超越时代之处在于,他在还没有电子计算机的时候,就划定了可计算问题的边界。