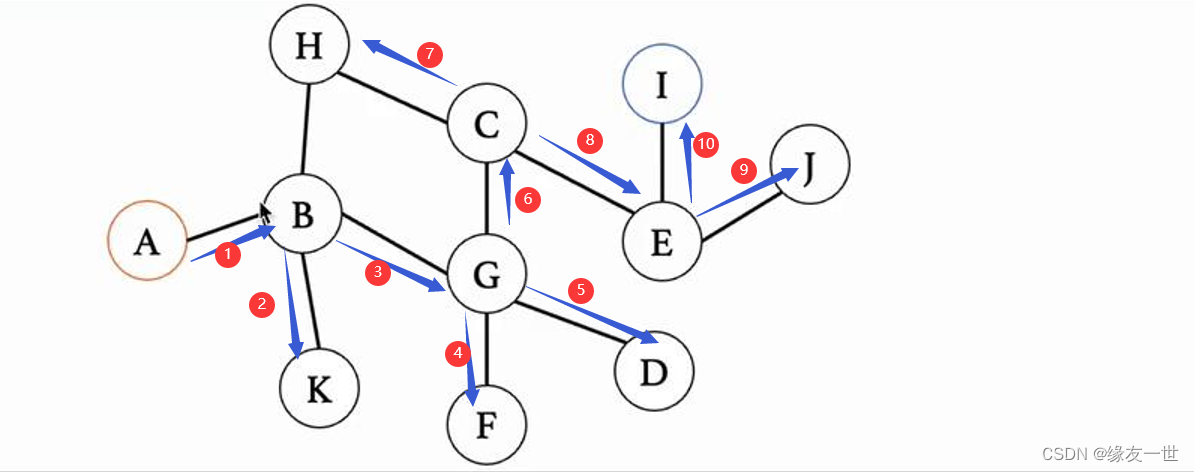
深度优先搜索[DFS]

并不唯一，只是一种情况 $A - > I$

实现代码

在这里插入图片描述

使用邻接表表示图。遍历的时间复杂度 $O (V + E)$ ；邻接矩阵的时间复杂度为 $O(V^2)$

#include <stdio.h>
#include <stdlib.h>
#define MaxVertex 5
typedef char E;
//结点和头节点分开定义，普通结点记录邻接顶点信息
typedef struct node {
    int nextVertex;
    struct node *next;
} *Node;
//头节点记录元素
struct HeadNode {
    E element;
    struct node * next;
};

typedef struct AdjacencyGraph {
    int vertexCount;//顶点数
    int edgeCount;//边数
    struct HeadNode vertex[MaxVertex];
}* Graph;
//初始化
Graph create();
//添加顶点
void addVertex(Graph graph,E element);
//添加边的关系
void addEdge(Graph graph,int a,int b);
//打印邻接表
void printGraph(Graph graph);
//深度优先搜索算法
int dfs(Graph graph,int startVertex,int targetVertex,int* visited);

#include "Map2.h"
//创建
Graph create() {
    Graph graph=(Graph) malloc(sizeof(struct AdjacencyGraph));
    graph->vertexCount=graph->edgeCount=0;
    return graph;
};
//添加顶点
void addVertex(Graph graph,E element) {
    if(graph->vertexCount>=MaxVertex) return;
    //添加新节点
    graph->vertex[graph->vertexCount].element=element;
    graph->vertex[graph->vertexCount].next=NULL;
    graph->vertexCount++;//顶点数更新
}
void addEdge(Graph graph,int a,int b) {
    //定义一个指向链表的头结点的下一结点指向
    Node node=graph->vertex[a].next;
    //开辟顶点空间
    Node newNode=(Node) malloc(sizeof(struct node));
    newNode->next=NULL;
    newNode->nextVertex=b;
    //如果头结点下面没有东西，就直接连接；否则，就遍历到最后一个结点后，添加新节点
    if(!node) {
        graph->vertex[a].next=newNode;//注意这里不能使用node，因为我们要真实地改变头节点的next指向
    }else {
        do{
            //如果已经连接到对应的结点，直接返回
            if(node->nextVertex==b) {
                free(newNode);
                newNode=NULL;
                return ;
            }
            //否则一直遍历到最后一个结点
            if(node->next) node=node->next;
            else break;//如果遭到了最后一个结点，直接结束
        }while(true);
        node->next=newNode;
    }
    graph->edgeCount++;//边数计数+1
}
//打印
void printGraph(Graph graph) {
    for(int i=0;i<graph->vertexCount;i++) {
        printf("%d | %c",i,graph->vertex[i].element);
        Node node=graph->vertex[i].next;
        while(node) {
            printf("-> %d",node->nextVertex);
            node=node->next;
        }
        printf("\n");
    }
}
/**
 * 深度优先搜索算法
 * @param graph 图
 * @param startVertex 起点顶点下标
 * @param targetVertex 目标顶点下标
 * @param visited 已到达过的顶点数组
 */
int dfs(Graph graph,int startVertex,int targetVertex,int* visited) {
    visited[startVertex]=1;//标记访问过的结点
    //大一当前结点
    printf("%c->",graph->vertex[startVertex].element);
    //如果当前顶点就是要找的顶点，就直接返回
    if(startVertex==targetVertex) return 1;
    //遍历当前顶点所有的分支
    Node node=graph->vertex[startVertex].next;
    while(node) {
        //如果已经到过[做的其他分支、回头路],就停止
        if(!visited[node->nextVertex]) {
            //没到过就继续往下走
            //如果查找成功就返回一，不用再看其他分支。
            if(dfs(graph,node->nextVertex,targetVertex,visited)) {
                return 1;
            }
        }
        node=node->next;
    }
    return 0;//当下的遍历都结束后，还是没有找到就返回零
}

#include "Map2.h"

int main() {
    Graph graph1 = create();
    for (int c = 'A'; c <= 'F'; c++) {
        addVertex(graph1, (char) c);
    }
    addEdge(graph1, 0, 1);//A->B
    addEdge(graph1, 1, 2);//B->C
    addEdge(graph1, 1, 3);//B->D
    addEdge(graph1, 1, 4);//D->E
    //addEdge(graph1, 4, 5);//E->F
    printGraph(graph1);
    int arr[graph1->vertexCount];
    for(int i=0;i<graph1->vertexCount;i++) {
        arr[i]=0;
    }
    printf("\n%d",dfs(graph1,0,5,arr));

    return 0;
}

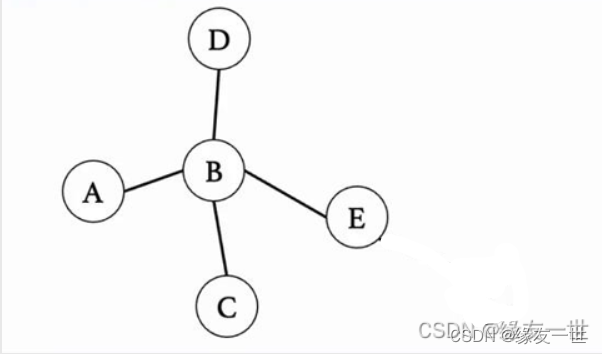
在这里插入图片描述

广度优先搜索【BFS】

先探索顶点的所有分支，然后再去看这些分支的所有分支。
实质上是更尽可能地探索更广的范围。

思路图解

$从A结点开始探索，A入队列。\\ 队列状态：A\\ 然后，再将其下一个结点B入队，A出队。\\ 队列状态：B\\$
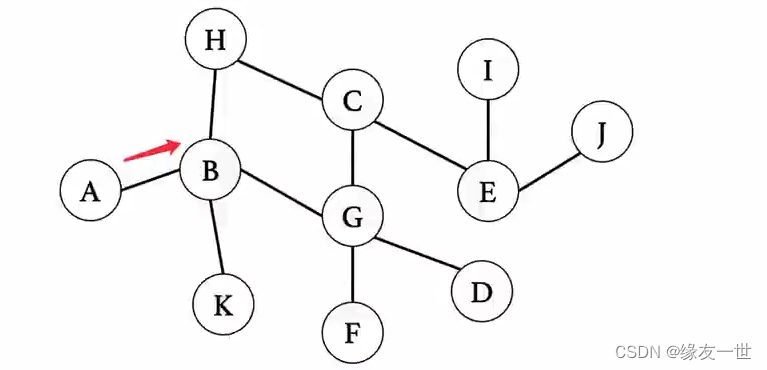
在这里插入图片描述
$将B的下一级结点入队\\ 队列状态：B->H->G->K\\ 将B出队\\ 队列状态：H->G->K$

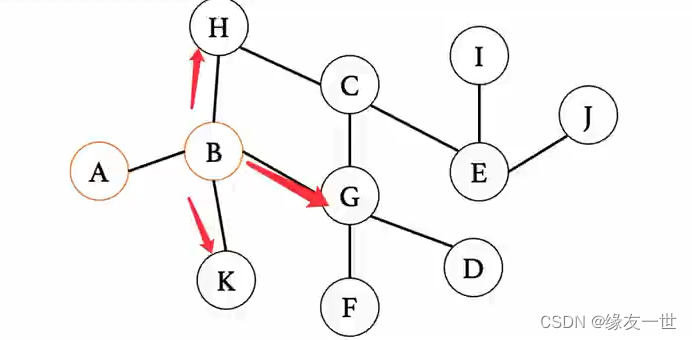
$依次按照队头到队尾的顺序，将其子节点入队，本结点出队。\\ C入队\\ 队列状态：H->G->K->C\\ H出队\\ 对列状态：G->K->C$

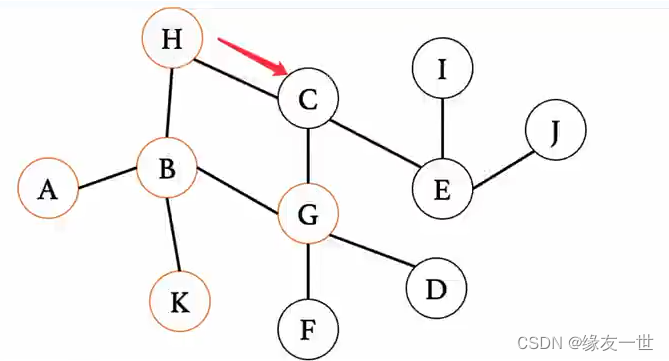
$D、F入队;C已入队，所以无需再次入队。\\ 队列状态：G->K->C->D->F\\ G出队\\ 对列状态：K->C->D->F\\$
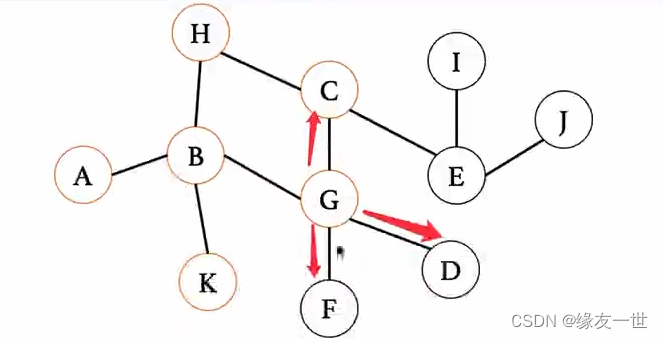
在这里插入图片描述
$K没有下一个结点，所以直接将K出队。\\ 队列状态：C->D->F$

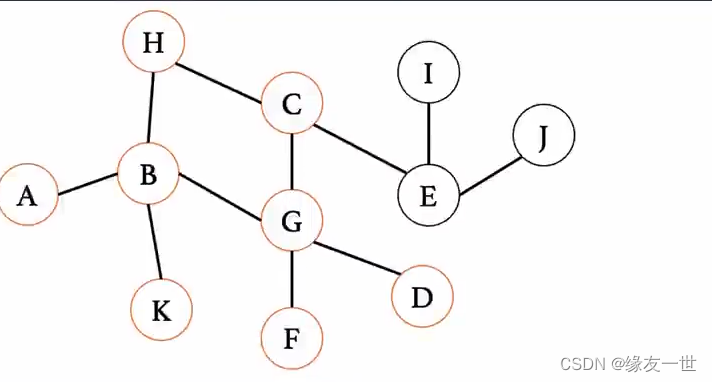
$再依次遍历队头的下一个结点\\ E入队\\ 队列状态：C->D->F->E C出队\\ 队列状态：D->F->E$

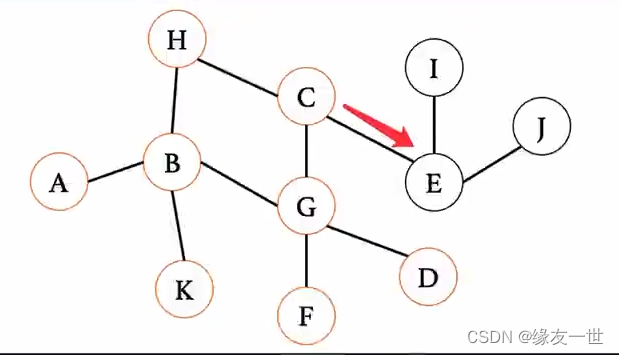
$因为D、F没有下一级邻接点，所以将D、F出队即可\\ 队列状态：E$

在这里插入图片描述
$I、J入队\\ 队列状态：E->I->J E出队\\ 队列状态：I->J$

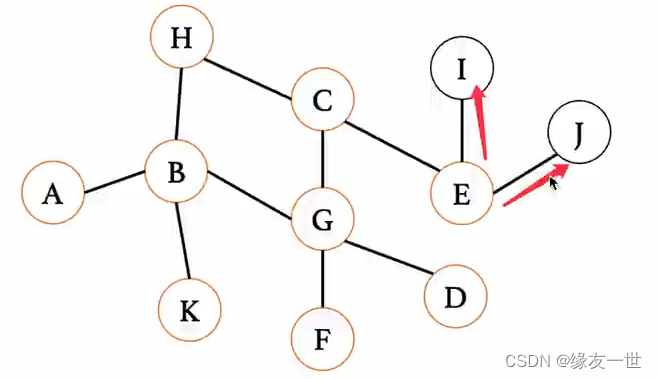
$最后再将队列的内容全部出队\\ 队列状态：空\\ 结束搜索$

代码实现·广度优先遍历【BFS】

存储结构：邻接表

图的结构

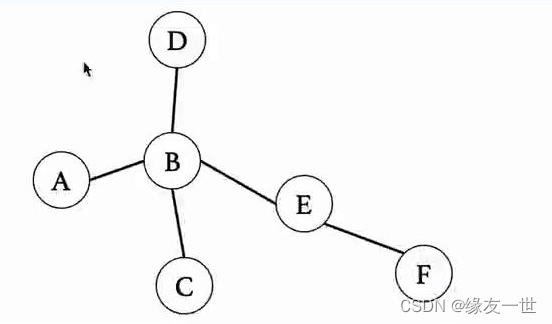
在这里插入图片描述

typedef int T;
struct QueueNode{
    T element;
    struct QueueNode * next;
};
typedef struct QueueNode* QNode;
struct Queue{
    QNode front,rear;
};
typedef struct Queue* LinkedQueue;
int initQueue(LinkedQueue queue) {
    QNode node=(QNode) malloc(sizeof(struct QueueNode));
    if(node==NULL) return 0;
    queue->front=queue->rear=node;
    return 1;
}

int offerQueue(LinkedQueue queue,T element) {
    QNode node=(QNode) malloc(sizeof(struct QueueNode));
    if(node== NULL) return 0;
    node->element=element;
    queue->rear->next=node;
    queue->rear=node;
    return 1;
}
int isEmpty(LinkedQueue queue){
    return queue->front==queue->rear;
};
T pollQueue(LinkedQueue queue) {
    T e=queue->front->next->element;
    QNode node=queue->front->next;
    queue->front->next=queue->front->next->next;
    if(queue->rear==node) queue->rear=queue->front;
    free(node);
    return e;
}

/**
 *
 * @param graph 图
 * @param startVertex 起点顶点下标
 * @param targetVertex 目标顶点下标
 * @param visited 已到达过的顶点数组
 * @param queue 辅助作用的队列
 * @return
 */
int bfs(Graph graph,int startVertex,int targetVertex,int* visited,LinkedQueue queue) {
    offerQueue(queue,startVertex);//头节点入队
    visited[startVertex]=1;//立马已标记
    //当队列不为空时，进行操作
    while(!isEmpty(queue)) {
        int next= pollQueue(queue);//从队列中取出一个顶点打印
        printf("%c->",graph->vertex[next].element);
        Node node=graph->vertex[next].next;//下一个结点
        //当当前结点的下一个结点存在时，进行入队操作
        while(node) {
            //如果找到目标结点，返回true
            if(node->nextVertex==targetVertex) return true;
            if(!visited[node->nextVertex]) {//!0==1未访问
                offerQueue(queue,node->nextVertex);//入队列
                visited[node->nextVertex]=1;//访问标记
            }
            node=node->next;//进行下一个结点
        }
    }
    return false;
}

Main.cpp

Graph graph1 = create();
for (int c = 'A'; c <= 'F'; c++) {
    addVertex(graph1, (char) c);
}
addEdge(graph1, 0, 1);//A->B
addEdge(graph1, 1, 2);//B->C
addEdge(graph1, 1, 3);//B->D
addEdge(graph1, 1, 4);//D->E
addEdge(graph1, 4, 5);//E->F
printGraph(graph1);
int arr1[graph1->vertexCount];
for(int i=0;i<graph1->vertexCount;i++) {
    arr1[i]=0;
}
struct Queue queue;
initQueue(&queue);
bfs(graph1,0,5,arr1,&queue);