二叉搜索树 bst 被递归地定义为具有以下属性的二叉树

节点的左子树仅包含键小于节点键的节点
a 的右子树节点只包含键大于或等于节点键的节点
左右子树也必须是二叉搜索树
完全二叉树cbt是一棵完全充满可能异常的树从左到右填充的底层

现在给定一系列不同的非负整数键，如果要求树也必须是你认为的cbt，则可以构造一个唯一的bst输出此 bst 的层序遍历序列

输入规范
每个输入文件包含一个测试用例，每个案例第一行包含一个正整数 n ≤ 1000 然后 n 个不同的非负整数keys在下一行给出，一行中的所有数字用空格分隔，并且不大于2000

输出规范

 这道题需要的操作时排序并且需要遍历，最重要的一点它是个完全二叉树，所以数组是最适合的

这道题我的思路来自于浙江大学课件7.0.2完全二叉树

解题思路 

这道题说白就是将输入的样例构造成一个完全搜索二叉树。因为完全线索二叉树的根节点一定是是一个处于左右子树中间的那个值（搜索二叉树其根节点要比自己的左子树上所有节点都大又要比自己右子树上所有节点都小）然后我们的思路就是在排好序的样例上每次去找一下当前函数所在的树的根节点然后将其插入二叉搜索树对应的位置，然后直接输出即可，因为此时我们构建的树数组只要我们顺序遍历就是层序遍历。

int n;
    cin>>n;
    for(int i=0;i<n;i++){
        int a;
        cin>>a;
        tree[i] = a;
    }
    //对输入样例排序
    sort(tree,tree+n,compare);
    solve(0,n-1,0);
    for(int i=0;i<n-1;i++)
        cout<<Ttree[i]<<" ";
    cout<<Ttree[n-1];

那么solve函数（排好序的样例上每次去找一下当前函数所在的树的根节点然后将其插入二叉搜索树对应的位置）该咋写呢？我们的思路是这样的，我们入函数的一定是所有样例，那么我们就是找整个样例的根节点，我们又知道根节点一定是是一个处于左右子树中间的那个值，然后我们的数组又是从0开始存值的，所以说其实在样例数组中左子树的个数加上此时这个树的左边界就可以确定此时这个树的根节点的值在样例数组的位置。

//得出左边节点个数
    int L = GetLeftLength(n);
    //左子树的个数就是此根节点的下标
    Ttree[rootIndex] = tree[L + Aleft];

然后我们找到最大的树的根节点，我们就可以继续递归去找它的左子树和右子树的根节点。这样这个函数该解决的问题就解决了。

//此节点的左节点在完全二叉树的下标
    int leftRootIndex = rootIndex * 2 + 1;
    //此节点的右节点在完全二叉树的下标
    int rightRootIndex = leftRootIndex + 1;
    solve(Aleft,Aleft+L-1,leftRootIndex);
    solve(Aleft+L+1,Aright,rightRootIndex);

但是如何找每个树的左子树的个数呢？

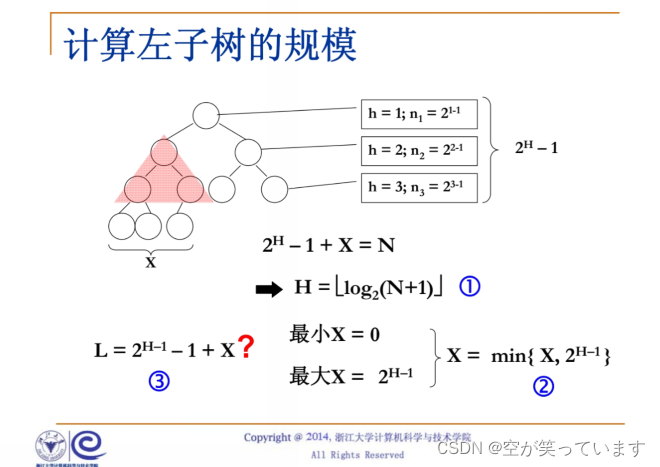
我们可以根据上图推出一个完全二叉树完美的那部分总共的个数(N)为pow（2,这个树的高度）-1+这个树减去完美部分的节点个数(X)，

 

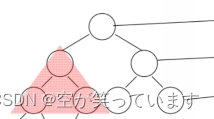
 然后我们就可以通过上述的公式推出 树的高度(h)=log2(N+1-X) ,然后我们就可以通过这个算出X，（但是我们题目中需要算出的是左子树节点个数如下图是不满足L(左子树个数)=pow(2,h-1)-1+X1（左子树除了完美部分之外的个数）这个公式的，因为很可能右边也有节点）

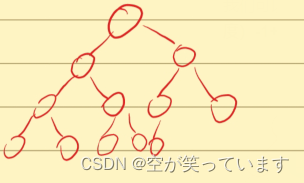（像这样的情况就不满足）

所以X1=min(X,左子树最大值(pow(2,h-1)))

然后就可以根据公式L(左子树个数)=pow(2,h-1)-1+X1写出函数。

int GetLeftLength(int n){
    //将完全二叉树完美的部分的高度求出，由2的h次方 -1 +x = n推出
    int h = log2(n+1);
    //求出左边除去完满二叉树部分多余的节点
    int x = n - pow(2,h) + 1;
    int a = pow(2,h-1);
    x = min(x,a);
    //多余的节点 + 完美二叉树左边一边的节点
    int L = a - 1 + x;
    return L;
}

下面是完整代码 

#include <iostream>
#include <cmath>
#include <algorithm>

using namespace std;
int compare(int a, int b){
    return a<b;
}
int tree[1001];
int Ttree[1001];
int GetLeftLength(int n){
    //将完全二叉树完美的部分的高度求出，由2的h次方 -1 +x = n推出
    int h = log2(n+1);
    //求出左边除去完满二叉树部分多余的节点
    int x = n - pow(2,h) + 1;
    int a = pow(2,h-1);
    x = min(x,a);
    //多余的节点 + 完美二叉树左边一边的节点
    int L = a - 1 + x;
    return L;
}
//后面的参数都是每次遍历时此时的树
//：Aleft:输入样例左边界，Aright:输入样例右边界，完全二叉树根节点下标
void solve(int Aleft,int Aright,int rootIndex){
    int n = Aright - Aleft + 1;
    // cout<<n<<endl;
    if(n==0) return;
    //得出左边节点个数
    int L = GetLeftLength(n);
    //左子树的个数就是此根节点的下标
    Ttree[rootIndex] = tree[L + Aleft];
    //此节点的左节点在完全二叉树的下标
    int leftRootIndex = rootIndex * 2 + 1;
    //此节点的右节点在完全二叉树的下标
    int rightRootIndex = leftRootIndex + 1;
    solve(Aleft,Aleft+L-1,leftRootIndex);
    solve(Aleft+L+1,Aright,rightRootIndex);
}
int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        int a;
        cin>>a;
        tree[i] = a;
    }
    //对输入样例排序
    sort(tree,tree+n,compare);
    solve(0,n-1,0);
    for(int i=0;i<n-1;i++)
        cout<<Ttree[i]<<" ";
    cout<<Ttree[n-1];
    return 0;
}