309.最佳买卖股票时机含冷冻期
力扣题目链接/文章讲解
视频讲解
记住昨天的回顾总结提到的:应该灵活利用 dp 数组的下标描述所有状态
动态规划五部曲
1、确定 dp 数组下标及值含义
dp[i][j],第 i 天状态为 j,所剩的最多现金为 dp[i][j]
这样,通过两个下标,能够描述在某天及当天的股票持有状态
每天具体可以区分出如下四个状态:
- 状态一:持有股票状态(今天买入股票,或者是之前就买入了股票然后没有操作,一直持有)
- 非冷冻期且不持有股票状态,需区分两种卖出股票状态(区分的原因:为了推冷冻期状态)
- 状态二:保持卖出股票的状态(两天前就卖出了股票,度过一天冷冻期。或者是前一天就是卖出股票状态,一直没操作)
- 状态三:今天卖出股票
- 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
dp[i][0]:下标表示在第 i 天,持有股票的状态,值为当前状态下的最大利润
dp[i][1]:下标表示在第 i 天,保持卖出股票的状态,值为当前状态下的最大利润
dp[i][2]:下标表示在第 i 天,当天卖出股票的状态,值为当前状态下的最大利润
dp[i][3]:下标表示在第 i 天,当前为冷冻期的状态,值为当前状态下的最大利润
2、确定递推公式
需要分别思考 dp[i][0]、dp[i][1]、dp[i][2]、dp[i][3] 应该怎么推
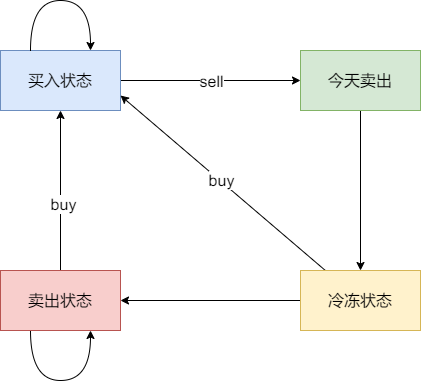
dp[i][0]:表示在第 i 天,持有股票的情况下的最大利润,我们需要考虑怎么从前一天转移到当前状态
- 可能在第 i - 1 天就已经持有股票了,即 dp[i - 1][0],到了第 i 天只需要保持状态不操作
- 可能在第 i - 1 天非冷冻期且不持有股票,那么我们可以在第 i 天买入,即 dp[i - 1][1] - prices[i]
- 可能在第 i - 1 天为冷冻期,我们也可以在第 i 天买入,即 dp[i - 1][3] - prices[i]
因为需要最大利润,所以 dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i])
dp[i][1]:表示在第 i 天,保持卖出股票的情况下的最大利润
- 可能在第 i - 1 天就已经保持卖出股票的状态了,即 dp[i - 1][1]
- 可能在第 i - 1 天为冷冻期,那么到了第 i 天就为非冷冻期且卖出股票的状态,即 dp[i - 1][3]
因为需要最大利润,所以 dp[i][1] = max(dp[i - 1][1], dp[i - 1][3])
dp[i][2]:表示在第 i 天,当天卖出股票的情况下的最大利润
这种只可能是在 i - 1 天持有股票的情况下,再在第 i 天卖出,即 dp[i][2] = dp[i - 1][0] + prices[i]
dp[i][3]:表示在第 i 天,当天为冷冻期的情况下的最大利润
这种只可能是在第 i - 1 天当天卖出的情况下,到了第 i 天才为冷冻期,即 dp[i][3] = dp[i - 1][2]
3、初始化 dp 数组
根据递推公式,第 i 天的 dp 值都是从第 i - 1 天的 dp 值推导出来的,我们需要初始化dp[0][j]
如果是持有股票状态(状态一)那么:dp[0][0] = -prices[0],一定是当天买入股票
保持卖出股票状态(状态二),这里其实从 「状态二」的定义来说 ,很难明确应该初始多少,这种情况我们就看递推公式需要我们给他初始成什么数值
如果 i 为 1,第 1 天买入股票,那么递归公式中需要计算 dp[i - 1][1] - prices[i] ,即 dp[0][1] - prices[1],那么大家感受一下 dp[0][1] (即第0天的状态二)应该初始成多少,只能初始为0。如果初始为其他数值,是我们第1天买入股票后手里还剩的现金数量就不对了
今天卖出了股票(状态三),同上分析,dp[0][2]初始化为0,dp[0][3]也初始为0
对于通过定义难以确定如何初始化的情况,应该结合递推公式确定如何初始化
4、确定遍历顺序
从递推公式可以看出 dp[i] 都是由 dp[i - 1] 推导出来的,那么一定是从前向后遍历
5、打印 dp 数组验证
代码如下
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
if (n == 0) return 0;
vector<vector<int>> dp(n, vector<int>(4, 0));
dp[0][0] -= prices[0]; // 持股票
for (int i = 1; i < n; i++) { // i为0时已经被初始化过了,从i为1开始遍历填充dp数组
// 四种情况
dp[i][0] = max(max(dp[i - 1][0], dp[i - 1][3] - prices[i]), dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));
}
};注意,最后的结果一定是到达最后一天,且不持有股票状态或冷冻期状态
714.买卖股票的最佳时机含手续费
力扣题目链接/文章讲解
视频讲解
本题假设在卖出的时候支付手续费
动态规划五部曲!
1、确定 dp 数组下标及值的含义
先想想本题 dp 应该怎么定义,别忘了之前说的,dp 数组的下标能够表示状态
在股票问题中,某个状态需要描述在某天,及是否持有股票
因此我们定义 dp 数组下标及值含义:
dp[i][0]:下标表示在第 i 天,未持有股票,值表示第 i 天未持有股票所得最多现金
dp[i][1]:下标表示在第 i 天,持有股票,值表示第 i 天持有股票所得最多现金
通过第一个下标 i 描述在哪一天,第二个下标为 0 或 1 描述在该天未持有或持有股票,这样通过两个下标就能够描述所有的状态了
2、确定递推公式
分别思考 dp[i][0] 和 dp[i][1] 分别应该怎么推
dp[i][0]:需要求第 i 天未持有股票所得最多现金,要考虑怎么转移到第 i 天未持有股票的这种状态
可能是在第 i 天卖出了股票,所得现金就是昨天持有股票,然后今天卖出股票后所得现金,注意考虑卖出需要支付手续费,即:dp[i - 1][1](昨天持有股票)+ prices[i](今天卖出股票)- fee
可能是在第 i - 1 天就未持有股票,那么就保持现状,所得现金就是昨天未持有股票的所得现金,即:dp[i - 1][0](昨天未持有股票)
因为求的最多现金,即 dp[i][0] = max(dp[i - 1][1] + prices[i] - fee[i], dp[i - 1][0])
同理,dp[i][1]:
可能是在第 i 天买入股票,所得现金为 dp[i - 1][0](昨天未持有股票)- prices[i](今天买入股票)(因为一只股票可以买卖多次,所以当第 i 天买入股票的时候,所持有的现金需要考虑之前买卖过的利润)
可能是在第 i - 1 天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金,即:dp[i - 1][1](昨天持有股票)
因为求的最多现金,即 dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][1])
3、dp 数组初始化
从递推公式看出,求某一天 dp 需要知道其前一天的 dp 值,即都是要从dp[0][0]和dp[0][1]推导出来
那么dp[0][0]表示第 0 天未持有股票,不持有股票现金就是 0,所以 dp[0][0] = 0
dp[0][1]表示第 0 天持有股票,持有股票一定是在第 0 天买入了股票,所以 dp[0][1] = -prices[0]
4、确定遍历顺序
从递推公式可以看出 dp[i] 都是由 dp[i - 1] 推导出来的,那么一定是从前向后遍历
5、打印 dp 数组验证
代码如下
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
vector<vector<int> > dp(prices.size(), vector<int>(2));
dp[0][0] = 0; // 第0天不持股
dp[0][1] = -prices[0]; // 第0天买入股票
for (int i = 1; i < prices.size(); ++i) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return max(dp[prices.size() - 1][0], dp[prices.size() - 1][1]);
}
};滚动数组优化的代码略
本题和 122.买卖股票的最佳时机II 的区别就是这里需要多一个减去手续费的操作
回顾总结
应该灵活利用 dp 数组的下标描述所有状态
对于定义难以确定如何初始化的情况,应该结合递推公式确定如何初始化