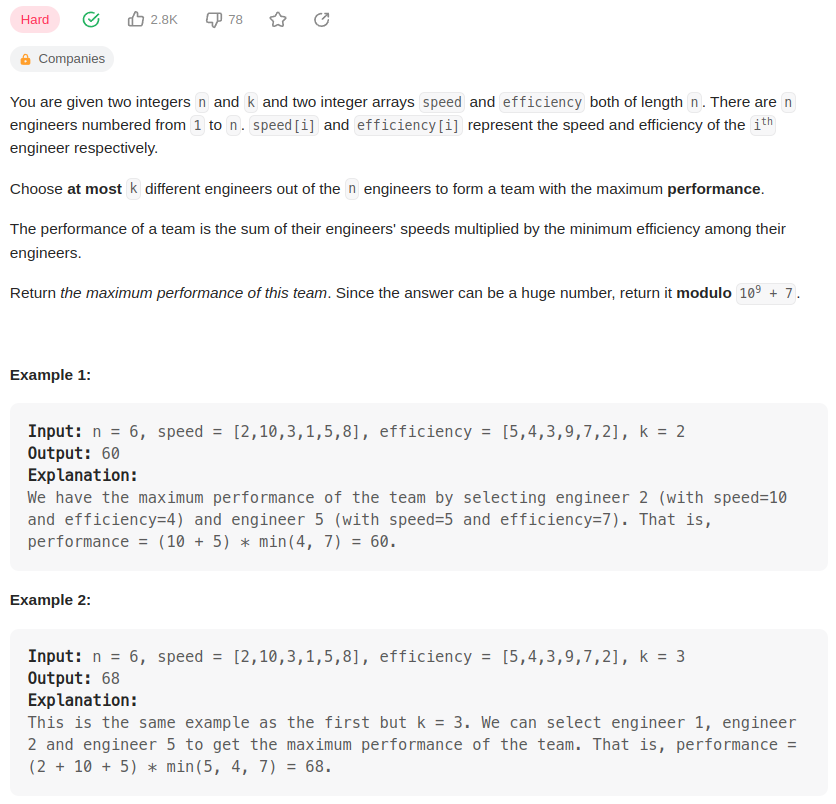
n个工程师，长度为n的speed数组和efficiency数组。
每次最多选k个工程师，取出k个对应的speed和efficiency数字。
performance=sum(k个speed) ✖ min(k个efficiency)
可以理解为k个人一起干，效率按最慢的人算（一个环节干不完其他人都要等）。
求最大的performance，结果对10⁹+7取模。

思路：

和2542题类似，
区别在于2542题不需要取mod，且固定是k个，本题是最多选k个。

因为受限于最小的efficiency, 所以把speed和efficiency的元素组对，按efficiency降序排序。
那么每次取出的是较大的efficiency, 同时也是对问题降维。
当选出的人数>k时，只需把较小的speed去掉即可, 这就需要用到最小堆。

每加一个，或者去掉一个工程师，都要更新sum.

由于不再是固定size为k, 所以每取一个组合，就要计算一次performance。

    public int maxPerformance(int n, int[] speed, int[] efficiency, int k) {
        PriorityQueue<Integer> pq = new PriorityQueue<>(k);
        long sum = 0;
        long res = 0;
        final int MOD = 1000000007;
        int[][] SEs = new int[n][2];
        for(int i = 0; i < n; i++) {
            SEs[i] = new int[]{speed[i], efficiency[i]};
        }

        Arrays.sort(SEs, (a,b)->(b[1] - a[1]));

        for(int i = 0; i < n; i++) {
            if(pq.size() >= k) sum -= pq.poll();
            sum += SEs[i][0];
            pq.offer(SEs[i][0]);
            
            res = Math.max(res, (sum * SEs[i][1]));
        }
        return (int)(res%MOD);
    }