最小生成树 Prim算法实现（c语言代码）

news2024/10/5 14:17:52

【问题描述】

城市之间的公路交通可以用一个无向图表示。如下图所示：  

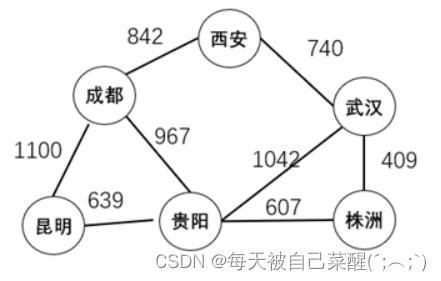
顶点表示城市、边表示城市之间有公路相连，边上的权值表示城市之间的公路长度。

编程解决以下问题：

（1）输入城市信息和城市之间公路的信息，建立图的邻接矩阵存储结构

 （2）为了使城市之间能够通信，将沿公路铺设光纤，给出合理的方案，使得光纤总耗费最小。

【输入形式】

第一行输入城市，城市之间用空格分开，输入q结束。

后面若干行，每行输入两座城市及城市间的公路长度，用空格分开。输入q结束。

输入起点城市名称。
【输出形式】起点城市出发得到的最小生成树，输出格式为(起点城市, 终点城市). 

注：城市之间是英文逗号，并且没有空格。
【样例输入】

成都 西安 昆明 贵阳 武汉 株洲 q

成都 西安 842

成都 昆明 1100

成都 贵阳 967

西安 武汉 740

贵阳 武汉 1042

贵阳 株洲 607

武汉 株洲 409

q

成都

注意事项

1. 录入边信息时，由于是无向图是对称矩阵，所以邻接矩阵对称位置都要记录边的权值。

2. 每加入一个顶点，所有未加入顶点都要更新 closedge 数组的内容。

在最后附有总的代码！！！

步骤：

一、建立图的邻接矩阵存储结构

1、定义图的数组存储的结构体类型。

#define MaxVertexNum 25 /*最大顶点数设为 25*/
#define INF 32767 		/*INF 表示∞*/
typedef int EdgeType; 	/*边的权值设为整型*/
typedef struct 			/*邻接矩阵类型定义*/
{
 char vexs[MaxVertexNum][10]; 				 /*顶点表成都,武汉...*/ 
 EdgeType edges[MaxVertexNum][MaxVertexNum]; /*邻接矩阵，即边表*/ 
 int n, e; 									 /*顶点数和边数*/
 }MGraph;

2、定义创建图的存储的函数。

/*返回顶点城市在顶点数组vexs 中序号，没有该城市名返回-1*/
int VexID(MGraph *G,char VexName[]) 
{
 int i; 
 for(i = 0; i < G -> n; i ++) 
 { 
	if(strcmp(VexName, G->vexs[i]) == 0) 
		break; 
 } 
 if(i == G->n) 
 	return -1; 
 else 
 	return i;
}

void createGraph(MGraph *G)
{
 int i, j, k, l; 
 char t[10], m[10]; 
 /*记录顶点信息*/
 printf("\n 请依次输入城市名，输入 q 退出：\n");
 for(i = 0; i < MaxVertexNum; i ++) 
 {
  	printf("\n 序号为%d的城市名称：", i); 
 	scanf("%s", G->vexs[i]); 
 	/***完善下列代码****/ /*如果输入q,退出循环*/
 	if(strcmp(G->vexs[i],"q")==0)	//比较字符串 
		break; 
 	G->n++; /*记录输入顶点数目*/	
 } 
 /*初始化邻接矩阵*/ 
/***完善下列代码****/     /*邻接矩阵主对角线上元素为0，其余为INF*/
	for(i=0;i<G->n;i++)
 	{
 		for(i=0;i<G->n;i++)
 		{
 			if(i==j)
 			{
 				G->edges[i][j] = 0;
			}
			else
				G->edges[i][j] = INF;
		}
	}
	/*记录边信息*/ 
     printf("\n 请输入边的信息，输入 q 退出：\n");    
  for(i = 0; ; i ++)                                   
   { 
	   	printf("\n 起始顶点：");   
	   	scanf("%s", t);   
	   	if(strcmp(t, "q") == 0)    
	   		break;   
	   	printf("\n 终止顶点：");   
	   	scanf("%s", m);   
	   	printf("\n 边的权重：");   
	   	scanf("%d", &l);    		
	    j = VexID(G, t);   
		k = VexID(G, m); 
	   	/***完善下列代码****/  ;/*在邻接矩阵对应位置记录边的权值*/ 
		if(j!=-1 && k!=-1)
		{
			G->edges[j][k] = l;		//无向图需要双向标记 
			G->edges[k][j] = l;	
			//G->e++;				//边数加一 
		}
		else
		{
			printf("输入的顶点信息有误！");	
			i--; 
		} 
	}  
	G->e = i;                  /*记录边的数目*/   	
}

二、编写最小生成树算法。

/*定义 Closedge 数组类型，作为普里姆算法的辅助数组类型*/
typedef struct         
{  
  int adjvex;  //目标点 
  int lowcost; //到目标点的最短距离 
}Closedge; 
/*输出最小生成树的普里姆算法。*/ 
void Prim(MGraph *G,char *startCity) 
{ /*G 为图的邻接矩阵存储，startCity 是起点城市名称*/  
  /*算法将依次输出需要铺设光缆的公路*/ 
	int k, j, i, minCost;  
	Closedge closedge[MaxVertexNum]; /*定义辅助数组*/  

	int v = VexID(G, startCity);
	if(v < 0) 
	{
		printf("输入的起点城市错误!\n");
		return;
	}
	closedge[v].lowcost = 0; 	//初始化所有的最短距离为0 
	for (j = 0; j < G->n; j ++) /*初始化 closedge 数组*/
   { /***完善下列代码****/
 		if(j!=v)		
 		{
 			closedge[j].adjvex = v;					//依此将顶点存入closedge数组 
			closedge[j].lowcost = G->edges[v][j];	//依此将边存入closedge数组 
		}	
	}	
	
	for (i = 1; i < G->n; i ++)  /*依次将顶点加入到集合 U 中*/  
	{ 
		for(j = 0; j < G->n; j++)/*定位第一个没有加入到 U 中的顶点*/    
			if(closedge[j].lowcost != 0)    
			{ 
				k = j;     
				break;    
			}			
		minCost = closedge[k].lowcost; /*定位V-U集合中 lowcost最小的顶点*/	  
		for (j = 0; j < G->n; j ++)    
			if (closedge[j].lowcost < minCost && closedge[j].lowcost != 0)             
			{
		 		/***完善下列代码****/
		 		k = j;
				minCost = closedge[j].lowcost;     
			}	
		printf("(%s,%s)\n", G->vexs[closedge[k].adjvex], G->vexs[k]);  /*输出新边加入到树中的边*/  
		/***完善下列代码****/   /*将该顶点加入到集合 U*/ 
		closedge[k].lowcost = 0; 		
		for (j = 0; j < G->n; j ++)     /*更新 closedge 数组的内容*/    
		{/***完善下列代码****/
 			if((G->edges[k][j] < closedge[j].lowcost)&& (G->edges[k][j] != 0 ))
 			{
 				closedge[j].adjvex = k;
 				closedge[j].lowcost = G->edges[k][j];
			}
		}
	}  	 
}

三、编写主函数

int main(int argn,char *argv[])
{
	int select, i, j;
	char c[10];
	MGraph *G;
	char startCity[1024];
	G = (MGraph *)malloc(sizeof(MGraph));
	G->n = G->e = 0;
	createGraph(G);
	fflush(stdin);
	gets(startCity);//输入出发城市
	Prim(G, startCity);
	return 0;
}

总的代码

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define MaxVertexNum 25 /*最大顶点数设为 25*/
#define INF 32767 		/*INF 表示∞*/
typedef int EdgeType; 	/*边的权值设为整型*/
typedef struct 			/*邻接矩阵类型定义*/
{
 char vexs[MaxVertexNum][10]; 				 /*顶点表成都,武汉...*/ 
 EdgeType edges[MaxVertexNum][MaxVertexNum]; /*邻接矩阵，即边表*/ 
 int n, e; 									 /*顶点数和边数*/
 }MGraph;
 
/*定义 Closedge 数组类型，作为普里姆算法的辅助数组类型*/
typedef struct         
{  
  int adjvex;  //目标点 
  int lowcost; //到目标点的最短距离 
}Closedge; 

 
 /*返回顶点城市在顶点数组vexs 中序号，没有该城市名返回-1*/
int VexID(MGraph *G,char VexName[]) 
{
 int i; 
 for(i = 0; i < G -> n; i ++) 
 { 
	if(strcmp(VexName, G->vexs[i]) == 0) 
		break; 
 } 
 if(i == G->n) 
 	return -1; 
 else 
 	return i;
}

void createGraph(MGraph *G)
{
 int i, j, k, l; 
 char t[10], m[10]; 
 /*记录顶点信息*/
 printf("\n 请依次输入城市名，输入 q 退出：\n");
 for(i = 0; i < MaxVertexNum; i ++) 
 {
  	printf("\n 序号为%d的城市名称：", i); 
 	scanf("%s", G->vexs[i]); 
 	/***完善下列代码****/ /*如果输入q,退出循环*/
 	if(strcmp(G->vexs[i],"q")==0)	//比较字符串 
		break; 
 	G->n++; /*记录输入顶点数目*/	
 } 
 /*初始化邻接矩阵*/ 
/***完善下列代码****/     /*邻接矩阵主对角线上元素为0，其余为INF*/
	for(i=0;i<G->n;i++)
 	{
 		for(i=0;i<G->n;i++)
 		{
 			if(i==j)
 			{
 				G->edges[i][j] = 0;
			}
			else
				G->edges[i][j] = INF;
		}
	}
	/*记录边信息*/ 
     printf("\n 请输入边的信息，输入 q 退出：\n");    
  for(i = 0; ; i ++)                                   
   { 
	   	printf("\n 起始顶点：");   
	   	scanf("%s", t);   
	   	if(strcmp(t, "q") == 0)    
	   		break;   
	   	printf("\n 终止顶点：");   
	   	scanf("%s", m);   
	   	printf("\n 边的权重：");   
	   	scanf("%d", &l);    		
	    j = VexID(G, t);   
		k = VexID(G, m); 
	   	/***完善下列代码****/  ;/*在邻接矩阵对应位置记录边的权值*/ 
		if(j!=-1 && k!=-1)
		{
			G->edges[j][k] = l;		//无向图需要双向标记 
			G->edges[k][j] = l;	
			//G->e++;				//边数加一 
		}
		else
		{
			printf("输入的顶点信息有误！");	
			i--; 
		} 
	}  
	G->e = i;                  /*记录边的数目*/   	
}


/*输出最小生成树的普里姆算法。*/ 
void Prim(MGraph *G,char *startCity) 
{ /*G 为图的邻接矩阵存储，startCity 是起点城市名称*/  
  /*算法将依次输出需要铺设光缆的公路*/ 
	int k, j, i, minCost;  
	Closedge closedge[MaxVertexNum]; /*定义辅助数组*/  

	int v = VexID(G, startCity);
	if(v < 0) 
	{
		printf("输入的起点城市错误!\n");
		return;
	}
	closedge[v].lowcost = 0; 	//初始化所有的最短距离为0 
	for (j = 0; j < G->n; j ++) /*初始化 closedge 数组*/
   { /***完善下列代码****/
 		if(j!=v)		
 		{
 			closedge[j].adjvex = v;					//依此将顶点存入closedge数组 
			closedge[j].lowcost = G->edges[v][j];	//依此将边存入closedge数组 
		}	
	}	
	
	for (i = 1; i < G->n; i ++)  /*依次将顶点加入到集合 U 中*/  
	{ 
		for(j = 0; j < G->n; j++)/*定位第一个没有加入到 U 中的顶点*/    
			if(closedge[j].lowcost != 0)    
			{ 
				k = j;     
				break;    
			}			
		minCost = closedge[k].lowcost; /*定位V-U集合中 lowcost最小的顶点*/	  
		for (j = 0; j < G->n; j ++)    
			if (closedge[j].lowcost < minCost && closedge[j].lowcost != 0)             
			{
		 		/***完善下列代码****/
		 		k = j;
				minCost = closedge[j].lowcost;     
			}	
		printf("(%s,%s)\n", G->vexs[closedge[k].adjvex], G->vexs[k]);  /*输出新边加入到树中的边*/  
		/***完善下列代码****/   /*将该顶点加入到集合 U*/ 
		closedge[k].lowcost = 0; 		
		for (j = 0; j < G->n; j ++)     /*更新 closedge 数组的内容*/    
		{/***完善下列代码****/
 			if((G->edges[k][j] < closedge[j].lowcost)&& (G->edges[k][j] != 0 ))
 			{
 				closedge[j].adjvex = k;
 				closedge[j].lowcost = G->edges[k][j];
			}
		}
	}  	 
} 



int main(int argn,char *argv[])
{
	int select, i, j;
	char c[10];
	MGraph *G;
	char startCity[1024];
	G = (MGraph *)malloc(sizeof(MGraph));
	G->n = G->e = 0;
	createGraph(G);
	fflush(stdin);
	gets(startCity);//输入出发城市
	Prim(G, startCity);
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/563880.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

2023最新SRC漏洞挖掘快速上手攻略！

2023最新SRC漏洞挖掘快速上手攻略！

前言 随着网络安全的快速发展&#xff0c;黑客攻击的手段也越来越多样化&#xff0c;因此SRC漏洞挖掘作为一种新的网络安全技术&#xff0c;也在不断发展和完善。那么&#xff0c;作为一个网安小白如果想要入门SRC漏洞挖掘&#xff0c;需要掌握哪些知识呢&#xff1f;以下是本…
阅读更多...
Vue3入门

Vue3入门

前言 在Vue 3提供的丰富的基础配置和插件生态系统之下&#xff0c;它是一种适用于多场景开发的前端框架&#xff0c;包括web应用程序、移动应用和桌面应用。使用Vue 3&#xff0c;您可以快速高效构建出具有优秀用户体验的应用程序。 准备工作 首先&#xff0c;我们需要安装V…
阅读更多...
运营-15.涉及促销活动的计算原则

运营-15.涉及促销活动的计算原则

1.是否 参与促销活动 如果商品参加促销活动&#xff0c;则在订单结算的时候显示已经参加的活动&#xff0c;否 则不显示&#xff1b; 2.是否 满足促销条件 如果有参加某个活动&#xff0c;则还要判断是否满足活动的条件&#xff0c;比如满200减 10&#xff0c;但是商品价格不足…
阅读更多...
spring-cloud-alibaba-seata分布式事务实例

spring-cloud-alibaba-seata分布式事务实例

第一步: 首先访问: https://seata.io/zh-cn/blog/download.html 下载我们需要使用的seata1.6.0服务 第二步: 1.在你的参与全局事务的数据库中加入undo_log这张表 -- for AT mode you must to init this sql for you business database. the seata server not need it. CRE…
阅读更多...
关于档案室十防环境监控的一些关键内容

关于档案室十防环境监控的一些关键内容

档案库房十防监控系统 智慧档案平台/温湿度/空气质量/漏水/视频/门禁/一体化管控平台 HONSOR多维空间可视化智慧档案库房建设一体化平台分享 三维可视化智慧档案馆库房一体化环境安全管控系统平台【相关项目经验图片/相关系统拓展图】【鉴赏】 1、智慧档案馆 2、智慧档案库房…
阅读更多...
从零开始之电机FOC控制

从零开始之电机FOC控制

我们将撕开FOC神秘而虚伪的面纱&#xff0c;以说人话的方式讲述它。真正的做到从零开始&#xff0c;小白一看就会&#xff0c;一学就废。 如果觉得有用的话&#xff0c;就点个赞呗&#xff0c;纯手码。 一、什么是FOC&#xff1f; FOC是Field Orientation Control的缩写&#…
阅读更多...
2023年，千万别裸辞....

2023年，千万别裸辞....

作为IT行业的大热岗位——软件测试&#xff0c;只要你付出了&#xff0c;就会有回报。说它作为IT热门岗位之一是完全不虚的。可能很多人回说软件测试是吃青春饭的&#xff0c;但放眼望去&#xff0c;哪个工作不是这样的呢&#xff1f;会有哪家公司愿意养一些闲人呢&#xff1f;…
阅读更多...
GaussDB云数据库SQL应用系列-基础使用

GaussDB云数据库SQL应用系列-基础使用

目录 一、前言 二、前提条件 1、连接数据库实例 2、GaussDB实例正常运行 三、操作示例 1、选择实例并进入SQL执行界面 2、创建数据库用户 3、创建数据库 4、创建SCHEMA 5、创建表&#xff08;增删改查&#xff09; 1&#xff09;创建3张表&#xff0c;并初始化一些数…
阅读更多...
Revit技巧 | 楼梯总画不好？原来是这些技巧你没有掌握

Revit技巧 | 楼梯总画不好？原来是这些技巧你没有掌握

Revit技巧 | 楼梯总画不好&#xff1f;原来是这些技巧你没有掌握 楼梯在我们BIM考试中是重点和难点&#xff0c;根据我们对历年考考题的分析&#xff0c;楼梯部分涉及到的考点为&#xff1a; 栏杆扶手样式的设置&#xff1b; 楼梯踏步数的设置&#xff1b; 楼梯踏板宽度的设…
阅读更多...
Adapt Learning使用教程（Adapt Framework/Adapt Authoring）（二）

Adapt Learning使用教程（Adapt Framework/Adapt Authoring）（二）

此文章在上一章的环境配置下操作的&#xff0c;如果还没配置参考我的上一篇文章&#xff1a;Adapt Learning使用教程&#xff08;Adapt Framework/Adapt Authoring&#xff09;&#xff08;一&#xff09; 。环境配置好了之后&#xff0c;就该从GitHub上拉取代码啦&#xff0c…
阅读更多...
如何入门Python——学习Python的指南针

如何入门Python——学习Python的指南针

✅作者简介&#xff1a;2022年博客新星 第八。热爱国学的Java后端开发者&#xff0c;修心和技术同步精进。 &#x1f34e;个人主页&#xff1a;Java Fans的博客 &#x1f34a;个人信条&#xff1a;不迁怒&#xff0c;不贰过。小知识&#xff0c;大智慧。 &#x1f49e;当前专栏…
阅读更多...
【JOSEF约瑟 应用于输配电路、变压器 JDP-1004双位置继电器 端子排】

【JOSEF约瑟 应用于输配电路、变压器 JDP-1004双位置继电器 端子排】

名称&#xff1a;双位置继电器&#xff1b;品牌&#xff1a;JOSEF约瑟&#xff1b;型号&#xff1a;JDP-1440&#xff1b;触点容量&#xff1a;250V2A&#xff1b;功率消耗&#xff1a;≤5W&#xff1b;额定电压&#xff1a;220V/110V&#xff1b;外形尺寸&#xff1a;868573特…
阅读更多...
LeetCode——矩阵中移动的最大次数

LeetCode——矩阵中移动的最大次数

目录 1、题目 2、题目解读 3、代码 1、题目 2684. 矩阵中移动的最大次数 - 力扣&#xff08;Leetcode&#xff09; 给你一个下标从 0 开始、大小为 m x n 的矩阵 grid &#xff0c;矩阵由若干 正 整数组成。 你可以从矩阵第一列中的 任一 单元格出发&#xff0c;按以下方式遍…
阅读更多...
面了一个00后测试工程师，问啥啥不会开口就要15k，我也是麻了····

面了一个00后测试工程师，问啥啥不会开口就要15k，我也是麻了····

在深圳这家金融公司也待了几年&#xff0c;被别人面试过也面试过别人&#xff0c;大大小小的事情也见识不少&#xff0c;今天又是团面的一天&#xff0c; 一百多个人都聚集在一起&#xff0c;因为公司最近在谈项目出来面试就2个人&#xff0c;无奈又被叫到面试房间。 整个过程我…
阅读更多...
一体化医学影像平台PACS源码，影像存档与传输系统源码

一体化医学影像平台PACS源码，影像存档与传输系统源码

PACS影像存档与传输系统源码 PACS即影像存档与传输系统&#xff0c;是医学影像、数字化图像技术、计算机技术和网络通讯技术相结合的产物&#xff0c;是处理各种医学影像信息的采集、存储、报告、输出、管理、查询的计算机应用程序。 是基于DICOM标准的医学影像管理系统&…
阅读更多...
分布式锁-Redis

分布式锁-Redis

一、为什么要有锁的概念 1.假如现在我们有这么一个场景&#xff1a; 用户在淘宝app上购买商品,用户提交订单的时候提交了,多点击了几次。 不管用户点击几次,只要用户一直停留在一个页面&#xff0c;那么就必须生成一个订单。 1.1 如果我们的服务是单体服务的话 比如现在我们的…
阅读更多...
单片机中GPIO八种工作模式详细分析

单片机中GPIO八种工作模式详细分析

今天给大家讲解一下 GPIO 基础&#xff0c;参考资料&#xff1a; STM32F1xx 官方资料&#xff1a; 《STM32中文参考手册V10》-第8章通用和复用功能IO(GPIO和AFIO) GPIO 是通用输入/输出端口的简称&#xff0c;是 STM32 可控制的引脚。GPIO 的引脚与外部硬件设备连接&#xff…
阅读更多...
2023护网蓝初面试题汇总

2023护网蓝初面试题汇总

一、描述外网打点的流程&#xff1f; 二、举几个 FOFA 在外网打点过程中的使用小技巧&#xff1f; 三、如何识别 CND &#xff1f; 四、邮件钓鱼的准备工作有哪些&#xff1f; 五、判断出靶标的 CMS &#xff0c;对外网打点有什么意义&#xff1f; 六、 Apache Log4j2…
阅读更多...
云原生之深入解析Kubernetes常见的多集群方案

云原生之深入解析Kubernetes常见的多集群方案

一、前言 Kubernetes 从 1.8 版本起就声称单集群最多可支持 5000 个节点和 15 万个 Pod&#xff0c;实际上应该很少有公司会部署如此庞大的一个单集群&#xff0c;很多情况下因为各种各样的原因我们可能会部署多个集群&#xff0c;但是又想将它们统一起来管理&#xff0c;这时…
阅读更多...
QT圆形进度条（QT桌面项目光照强度检测）

QT圆形进度条（QT桌面项目光照强度检测）

文章目录 前言一、编程思路二、核心代码实现总结 前言 本篇文章我们讲解QT实现圆形进度条&#xff0c;并实现动态的效果。 一、编程思路 实现QT圆形进度条其实是非常简单的&#xff0c;思路就是画两个圆弧。 这里大家就会觉得很奇怪了为什么画两个圆弧就能实现圆形进度条了呢…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023