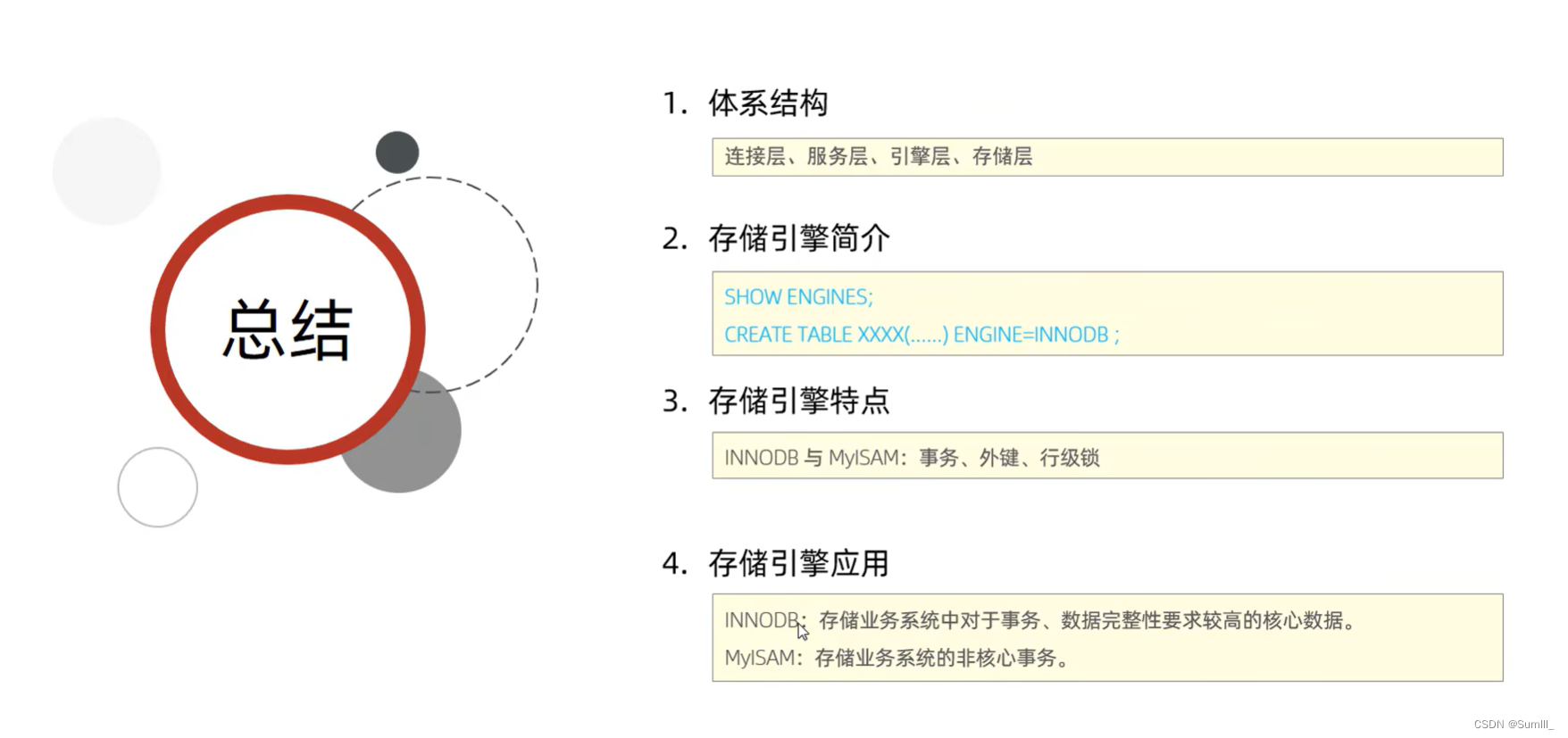
目录

1、题目

 2、题目解读

 3、代码

---

1、题目

2684. 矩阵中移动的最大次数 - 力扣（Leetcode）

给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干 正 整数组成。

你可以从矩阵第一列中的 任一 单元格出发，按以下方式遍历 grid ：

• 从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。

返回你在矩阵中能够 移动 的 最大 次数。

示例 1：

输入：grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
输出：3
解释：可以从单元格 (0, 0) 开始并且按下面的路径移动：
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
可以证明这是能够移动的最大次数。

示例 2：

输入：grid = [[3,2,4],[2,1,9],[1,1,7]]
输出：0
解释：从第一列的任一单元格开始都无法移动。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 106

 2、题目解读

题目第二个示例，第一列中的3的左边还有左下角都比3小，不能移动。2和1也是如此，所以无法移动

理解题目意思，然后就是dfs，每一轮向右搜索一列。注意不要重复搜索！

 3、代码

class Solution {
      //dfs
    private int n;
    private int m;
    private int max=0;//保存 当前最大移动次数

    public int maxMoves(int[][] grid) {
        n=grid.length;
        m=grid[0].length;
        //vis用于剪枝操作
        boolean[][] vis = new boolean[n][m];
        for(int i=0;i<n;i++)
        {
            dfs(i,0,grid, vis);
            //如果max为m-1，已经是能达到的最大值了，无须再考虑后面的情况了
            if(max==m-1)
                break;
        }
        return max;
    }
    public void dfs(int i, int j, int[][] grid, boolean[][] vis)
    {
        //如果j达到最大值，说明可以移动到最后一列，此时就可以退出递归了
        if(j==m-1)
        {
            max=m-1;
            return;
        }
        //符合移动条件，且目标单元格还没有搜索过
        if(grid[i][j+1]>grid[i][j] && !vis[i][j + 1])
        {
            //继续搜索
            dfs(i,j+1,grid,vis);
            //并标记目标单元格已经搜索，避免重复搜索
            vis[i][j+1]=true;
        }
        //下面同理
        if(i>0 && grid[i-1][j+1]>grid[i][j] && !vis[i - 1][j + 1])
        {
            dfs(i-1,j+1,grid,vis);
            vis[i-1][j+1]=true;
        }
        if(i<n-1 && grid[i+1][j+1]>grid[i][j] && !vis[i + 1][j + 1])
        {
            dfs(i+1,j+1,grid,vis);
            vis[i+1][j+1]=true;
        }
        //全部搜索完毕后，若j值比max大，则保留该j值为最大值
        max=Math.max(max,j);
    }
}