动态规划算法,以最小的消耗解题!
以一个走楼梯为例子展开。
假设有一个三级台阶,我们一次可以走一步,或者一次走两步,那么由此可知,一共有3中走法,如下图

当台阶数量少的时候,确实很容易解出来;那如果台阶数量是5呢,是10呢,是20呢。。。
这样复杂程度就蹭蹭蹭的放上涨了,这时就很那靠脑力算出来,所以得靠程序算法去求解。
可以使用递归的思维去求解!
从上往下分析问题,大问题可以分解为子问题,子问题中还有更小的子问题
比如总共有 5 级台阶,求有多少种走法;由于一次可以走两级台阶,也可以走一级台阶,所以我们可以分成两个情况
- 最后一次走了两级台阶,问题变成了“走上一个 3 级台阶,有多少种走法?”
- 最后一步走了一级台阶,问题变成了“走一个 4 级台阶,有多少种走法?”
我们将求 n 级台阶的共有多少种走法用 f(n) 来表示,则 f(n) = f(n-1) + f(n-2);
由上可得
f(5) = f(4) + f(3);
f(4) = f(3) + f(2);
f(3) = f(2) + f(1);
边界情况分析
走一步台阶时,只有一种走法,所以 f(1)=1
走两步台阶时,有两种走法,直接走 2 个台阶,分两次每次走 1 个台阶,所以 f(2)=2
走两个台阶以上可以分解成上面的情况
所以使用递归实现代码如下:
int WalkCount(int n) {
if (n <= 0) return 0;
if (1 == n) { // 一级台阶,一种走法
return 1;
} else if (2 == n) {
return 2; // 二级台阶,二种走法
}
// f(n) = f(n-1) + f(n-2);
return WalkCount(n - 1) + WalkCount(n - 2);
}编写main方法进行测试:
int main(void) {
int n = 0;
printf("请输入台阶的级数:");
scanf_s("%d", &n);
for (int i = 0; i <= n; i++) {
printf("走 %d 级台阶共有 %d 当中走法!\n", i, WalkCount(i));
}
return 0;
}编译输出:
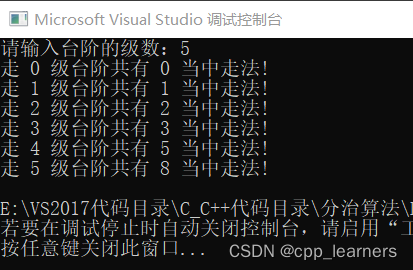

确实可以计算出来,但这种方式有种问题!
细心的朋友是否会注意到,上面的代码中存在很多重复的计算?
比如: f(5) = f(4) + f(3)
计算分成两个分支:
f(4) = f(3)+f(2) = f(2) + f(1) + f(2);
f(3) = f(2) + f(1);
上面阴影的部分就是重复计算的一部分!
有没有办法避免重复计算的部分?
其实我们可以从下向上分析推断问题。
f(1) = 1 f(2) = 2
f(3) = f(1) + f(2) = 3
f(4) = f(3) + f(2) = 3 + 2 = 5
f(5) = f(4) + f(3) = 5 + 3 = 8
依次类推 ...
我们可以不使用递归,从下往上进行分析推断问题,可以定义一个数组将之前计算好的数据保存下来,等到上面需要使用时,直接提取出来计算即可!
实现代码如下:
long long WalkCount2(int n) {
if (0 >= n) return 0;
if (1 == n) return 1;
if (2 == n) return 2;
long long *arr = (long long *)malloc(sizeof(long long)*(n + 1));
memset(arr, 0, sizeof(n)*(n + 1));
*(arr + 0) = 0; // arr[0] = 0;
*(arr + 1) = 1; // arr[1] = 1;
*(arr + 2) = 2; // arr[2] = 2;
for (int i = 3; i <= n; i++) {
// arr[3] = arr[i-1] + arr[i-2];
*(arr + i) = *(arr + (i-1)) + *(arr + (i-2));
}
long long ret = *(arr + n);
free((void *)arr);
return ret;
}使用以下代码进行测试:
int main(void) {
int n = 0;
printf("请输入台阶的级数:");
scanf_s("%d", &n);
for (int i = 0; i <= n; i++) {
printf("走 %d 级台阶共有 %lld 当中走法!\n", i, WalkCount2(i));
}
return 0;
}运行截图:
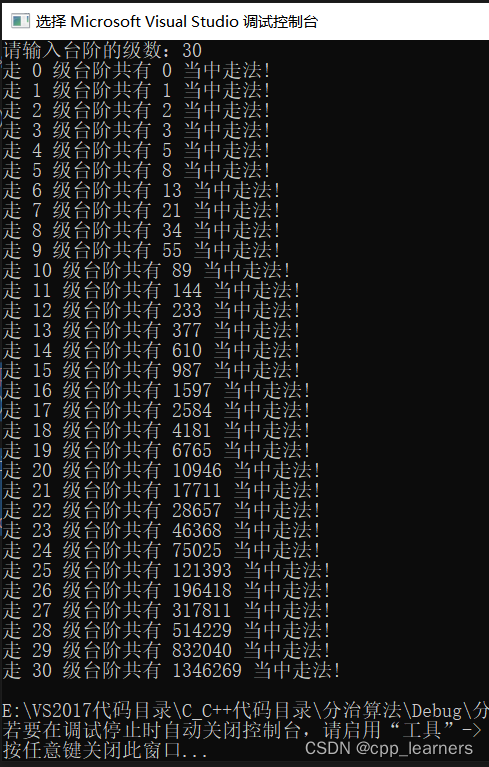
可以很快速的计算出来。
还可以计算更大的数据,例如1000次,只要计算的数据long long类型可以存储,那么都是可以很快的计算出来,但如果是递归,则需要花费很多时间,因为他在做重复的计算工作!
动态规划算法实现就是类似这样;当然并不是所有的递归都可以使用动态规划算法来实现,得要有重复计算的才可以!








![[附源码]Python计算机毕业设计SSM考勤管理系统(程序+LW)](https://img-blog.csdnimg.cn/361e94cb3715465597ada5cfab386e4b.png)

