论文信息
《Disentangled Information Bottleneck》
论文地址:https://ojs.aaai.org/index.php/AAAI/article/view/17120
代码地址:GitHub - PanZiqiAI/disentangled-information-bottleneck
@inproceedings{pan2021disentangled,
title={Disentangled information bottleneck},
author={Pan, Ziqi and Niu, Li and Zhang, Jianfu and Zhang, Liqing},
booktitle={Proceedings of the AAAI Conference on Artificial Intelligence},
volume={35},
number={10},
pages={9285–9293},
year={2021}
}
内容理解
摘要
信息瓶颈(Information Bottleneck,IB)方法是一种从源随机变量中提取与预测目标随机变量相关的信息的技术,通常通过优化平衡压缩项和预测项的IB拉格朗日量(IB Lagrangian)来实现。然而,IB拉格朗日量很难优化,需要对拉格朗日乘子的调整值进行多次试验。此外,我们还表明,在优化IB Lagrangian的过程中,随着压缩的增强,预测性能会严格下降。在本文中,我们从监督解纠缠的角度实现了IB方法。具体来说,我们引入了解纠缠信息瓶颈(DisenIB),它能最大限度地压缩源而不损失目标预测性能(最大压缩)。理论和实验结果表明,我们的方法在最大压缩方面是一致的,并且在泛化、对抗性攻击的鲁棒性、分布外检测和监督解纠缠方面表现良好。
引言
信息压缩重要的是决定数据的哪些方面应该保留,哪些方面应该丢弃。
IB就提供了应对这个问题的原则,它压缩源随机变量去保留与目标随机变量的相关信息,并同时丢弃所有的不相关信息。研究还表明,IB能够很好的产生广义的表示(表征学习)。
给定两个随机变量X,Y,IB旨在压缩X到一个瓶颈随机变量T,该变量保留了和预测值Y相关的信息。即,探索一个概率映射
q
(
T
∣
X
)
q(T|X)
q(T∣X),使得
I
(
X
;
T
)
I(X;T)
I(X;T)受到约束,同时
I
(
T
;
Y
)
I(T;Y)
I(T;Y)被最大化:
arg max
T
∈
Δ
I
(
T
;
Y
)
,
s
.
t
.
I
(
X
;
T
)
≤
r
\begin{equation} \argmax_{T \in \Delta} I(T;Y), \ s.t. \ I(X;T) \leq r \end{equation}
T∈ΔargmaxI(T;Y), s.t. I(X;T)≤r
其中 r 限制了压缩水平。
在实践中为了避免非线性约束,可以通过最小化所谓的IB拉格朗日量来优化Eq(1):
L
I
B
[
q
(
T
∣
X
)
;
β
]
=
−
I
(
T
;
Y
)
+
β
I
(
X
;
T
)
\begin{equation} \mathcal{L}_{IB}[q(T|X);\beta] = -I(T;Y) + \beta I(X;T) \end{equation}
LIB[q(T∣X);β]=−I(T;Y)+βI(X;T)
其中,
β
∈
[
0
,
1
]
\beta \in [0, 1]
β∈[0,1]是控制平衡的拉格朗日参数。
最小化Eq(2)会存在下列问题:
- 很难得到期望的压缩水平r。有工作认为 β \beta β跟压缩水平没有关系,需要对不同的 β \beta β值做多次优化才能达到特定的压缩水平。
- 压缩不可避免地降低了预测性能。
作者期望:
- 在X压缩为T的过程中从Y中提取最小有效部分,即最大程度的压缩X而不减少 I ( T ; Y ) I(T;Y) I(T;Y),即最大压缩。
- 消除对多次优化的需求,探索一种通过单一优化实现最大压缩的方法
有监督解纠缠解决了识别互补数据方面并在监督下将其彼此分离的问题。类似地,在IB方法中,必须将Y-relevant和Y-irrelevant的数据方面分开。这启发了作者从监督解纠缠的角度来实现IB方法,因此提出的解纠缠信息瓶颈(Disentangled Information Bottleneck,DisenIB)。据所知,该工作是第一个将IB方法与监督解纠缠联系起来的。贡献:
- 研究了IB拉格朗日中的权衡,表明平衡压缩和预测项只能降低预测性能,因此无法实现最大压缩。
- 提出了IB的一个变体,即纠缠信息瓶颈(DisenIB),它被证明在最大压缩上是一致的。具体来说,DisenIB消除了对多次优化的需求,并通过一次优化实现了一致的最大压缩。
- 通过实验结果,证明了这篇文章的理论陈述是正确的,并表明DisenIB在泛化、对抗性攻击的鲁棒性和分布外数据检测以及监督解纠缠方面表现良好。
方法
IB Lagrangian中压缩项与预测项的权衡
IB Lagrangian中存在的压缩项与预测项之间的权衡问题。具体而言,通过优化IB拉格朗日量获得的压缩和预测目标的最优解始终低于通过独立优化每个目标获得的最优解:

结果表明IB Lagrangian最优解是随着压缩程度
β
\beta
β的增大而严格下降的,即,压缩只能降低预测性能,这是不希望发生的。
最大压缩的一致性
由于上述权衡,优化IB Lagrangian不能实现最大压缩。期望探索一种能够进行最大压缩的方法。此外,这篇文章还希望消除对多重优化的需求。也就是说,希望探索一种通过单一优化一致地执行最大压缩的方法,这被称为最大压缩的一致性属性。
首先考虑最大压缩的情况,即
I
(
X
;
Y
)
=
H
(
Y
)
I(X;Y)=H(Y)
I(X;Y)=H(Y)。根据互信息(Mutual Information,MI)的基本性质,可以知道当
I
(
T
;
Y
)
=
H
(
Y
)
I(T;Y)=H(Y)
I(T;Y)=H(Y)时表示没有预测损失的情况。
根据信息处理不等式和MI的基本性质可知在无损预测的情况下,有:
H
(
Y
)
=
I
(
T
;
Y
)
⩽
I
(
X
;
T
)
⩽
H
(
X
)
\begin{equation} H(Y)=I(T ; Y) \leqslant I(X ; T) \leqslant H(X) \end{equation}
H(Y)=I(T;Y)⩽I(X;T)⩽H(X)
则在最大压缩的情况下有:
I
(
X
;
T
)
=
I
(
T
;
Y
)
=
H
(
Y
)
\begin{equation} I(X ; T)=I(T ; Y)=H(Y) \end{equation}
I(X;T)=I(T;Y)=H(Y)
因此,最大压缩一致性的形式定义如下:

满足
I
(
X
;
T
)
=
I
(
T
;
Y
)
=
H
(
Y
)
I(X ; T)=I(T ; Y)=H(Y)
I(X;T)=I(T;Y)=H(Y)涉及的精确信息量的控制,即将
I
(
X
;
T
)
I(X;T)
I(X;T)和
I
(
T
;
Y
)
I(T;Y)
I(T;Y)都精确约束在
H
(
Y
)
H(Y)
H(Y)。
Disentangled IB(DisenIB)
将Y中的相关信息编码为T,不相关信息编码为S,则要最小化的目标函数如下:
L
DisenIB
[
q
(
S
∣
X
)
,
q
(
T
∣
X
)
]
=
−
I
(
T
;
Y
)
−
I
(
X
;
S
,
Y
)
+
I
(
S
;
T
)
\begin{equation} \mathcal{L}_{\text {DisenIB }}[q(S \mid X),\ q(T \mid X)] = -I(T ; Y)-I(X ; S, Y)+I(S ; T) \end{equation}
LDisenIB [q(S∣X), q(T∣X)]=−I(T;Y)−I(X;S,Y)+I(S;T)
具体来说:
- 通过最大化 I ( X ; S , Y ) I(X;S,Y) I(X;S,Y),来鼓励(S, Y)来表示X的整体信息,使得S至少覆盖了Y-irrelevant部分的数据信息。
- 通过最大化 I ( T ; Y ) I(T;Y) I(T;Y),来鼓励T能准确的解码Y,这样T至少涵盖了Y-relevant部分的数据信息。
- 通过最小化 I ( S ; T ) I(S;T) I(S;T)来迫使S与T分离,消除他们之间重叠的信息,从而收紧边界,使得T中包含与Y相关的信息,S中包含与Y不相关的信息。
具体实施细节
根据推导可知,最小化
−
I
(
T
;
Y
)
−
I
(
X
;
S
,
Y
)
-I(T ; Y)-I(X ; S, Y)
−I(T;Y)−I(X;S,Y)等于:
min
q
,
p
,
r
E
p
data
(
x
)
E
p
data
(
y
∣
x
)
[
−
E
q
(
t
∣
x
)
log
p
(
y
∣
t
)
−
E
q
(
s
∣
x
)
log
r
(
x
∣
s
,
y
)
]
\begin{equation} \min _{q, p, r} \mathbb{E}_{p_{\text {data }}(x)} \mathbb{E}_{p_{\text {data }}(y \mid x)}\left[-\mathbb{E}_{q(t \mid x)} \log p(y \mid t)-\mathbb{E}_{q(s \mid x)} \log r(x \mid s, y)\right] \end{equation}
q,p,rminEpdata (x)Epdata (y∣x)[−Eq(t∣x)logp(y∣t)−Eq(s∣x)logr(x∣s,y)]
首先,概率映射
q
(
t
∣
x
)
q(t|x)
q(t∣x)和
q
(
s
∣
x
)
q(s|x)
q(s∣x)有两个编码器参数化:
E
t
:
X
→
R
K
E_t:\mathcal{X} \rightarrow \mathbb{R}^K
Et:X→RK 和
E
s
:
X
→
R
K
E_s:\mathcal{X} \rightarrow \mathbb{R}^K
Es:X→RK ,其中
E
t
E_t
Et和
E
s
E_s
Es分别被用来产生瓶颈表示 t(relevant)和 s(irrelevant),K是瓶颈表示的维度。因为在确定性的场景中(即,t是x的确定性函数),互信息
I
(
X
;
T
)
I(X;T)
I(X;T)是分段常数,难以通过梯度回传进行优化,所以引入高斯噪声
N
(
0
,
σ
1
2
I
)
\mathcal{N}\left(\mathbf{0}, \sigma_1^2 \mathbf{I}\right)
N(0,σ12I)使得
E
t
E_t
Et和
E
s
E_s
Es是随机的,重新参数化技巧去产生t和s:
t
∼
E
t
(
x
)
+
N
(
0
,
σ
1
2
I
)
s
∼
E
s
(
x
)
+
N
(
0
,
σ
2
2
I
)
t \sim E_{\mathrm{t}}(x)+\mathcal{N}\left(\mathbf{0}, \sigma_1^2 \mathbf{I}\right) \\ s \sim E_{\mathrm{s}}(x)+\mathcal{N}\left(\mathbf{0}, \sigma_2^2 \mathbf{I}\right)
t∼Et(x)+N(0,σ12I)s∼Es(x)+N(0,σ22I)
变分近似通过解码器来参数化:
D
:
R
K
→
R
∣
Y
∣
D: \mathbb{R}^K \rightarrow \mathbb{R}^{|\mathcal{Y}|}
D:RK→R∣Y∣,产生可能结果是y的概率。在分类任务中,很容易发现
−
E
p
data
(
y
∣
x
)
E
q
(
t
∣
x
)
log
p
(
y
∣
t
)
-\mathbb{E}_{p_{\text {data }}(y \mid x)} \mathbb{E}_{q(t \mid x)} \log p(y \mid t)
−Epdata (y∣x)Eq(t∣x)logp(y∣t)就是CrossEntropy Loss(交叉熵损失):
L
C
E
(
D
(
E
t
(
x
)
)
,
y
)
=
−
log
D
(
E
t
(
x
)
)
y
\begin{equation} \mathcal{L}_{\mathrm{CE}}\left(D\left(E_{\mathrm{t}}(x)\right), y\right)=-\log D\left(E_{\mathrm{t}}(x)\right)_y \end{equation}
LCE(D(Et(x)),y)=−logD(Et(x))y
即最大化 I ( T ; Y ) I(T;Y) I(T;Y)在分类任务中即对应着最小化相应的交叉熵损失,回归任务中可以考虑L1和MSE。
对于最大化
I
(
X
;
S
,
Y
)
I(X;S,Y)
I(X;S,Y),考虑一个重构器:
R
:
R
K
×
Y
→
X
R: \mathbb{R}^K \times \mathcal{Y} \rightarrow \mathcal{X}
R:RK×Y→X,接收concat的(s, t)作为输入,并产生相应的重构。所以重构损失可以用作
−
E
p
data
(
y
∣
x
)
E
q
(
s
∣
x
)
log
r
(
x
∣
s
,
y
)
-\mathbb{E}_{p_{\text {data }}(y \mid x)} \mathbb{E}_{q(s \mid x)} \log r(x \mid s,\ y)
−Epdata (y∣x)Eq(s∣x)logr(x∣s, y):
L
recon
(
R
(
E
s
(
x
)
,
y
)
,
x
)
=
∥
R
(
E
s
(
x
)
,
y
)
−
x
∥
2
2
\begin{equation} \mathcal{L}_{\text {recon }}\left(R\left(E_{\mathrm{s}}(x), y\right), x\right)=\left\|R\left(E_{\mathrm{s}}(x), y\right)-x\right\|_2^2 \end{equation}
Lrecon (R(Es(x),y),x)=∥R(Es(x),y)−x∥22
最小化
I
(
S
;
T
)
I(S;T)
I(S;T),可以通过鉴别器d和对抗性训练来实现:
min
q
max
d
E
q
(
s
)
q
(
t
)
log
d
(
s
,
t
)
+
E
q
(
s
,
t
)
log
(
1
−
d
(
s
,
t
)
)
\begin{equation} \min _q \max _d \mathbb{E}_{q(s) q(t)} \log d(s, t)+\mathbb{E}_{q(s, t)} \log (1-d(s, t)) \end{equation}
qmindmaxEq(s)q(t)logd(s,t)+Eq(s,t)log(1−d(s,t))
其中,鉴别器d通过
W
:
R
2
K
→
R
W: \mathbb{R}^{2 K} \rightarrow \mathbb{R}
W:R2K→R来参数化,接收concat的(s, t)作为输入,并产生相应的概率估计,输入是来自
q
(
s
,
t
)
q(s, t)
q(s,t)而不是来自
q
(
s
)
q
(
t
)
q(s)q(t)
q(s)q(t)的概率。首先从联合分布
q
(
s
,
t
)
q(s, t)
q(s,t)中有效地进行采样,方法是首先从数据集中均匀随机地对
x
x
x进行采样,然后从
q
(
s
,
t
∣
x
)
q(s, t|x)
q(s,t∣x)中进行采样,然后通过沿批轴从联合分布
q
(
s
)
q
(
t
)
q(s)q(t)
q(s)q(t)中打乱样本,从边际分布
q
(
s
)
q
(
t
)
q(s)q(t)
q(s)q(t)的乘积中抽样。
对应的大致框架如下:
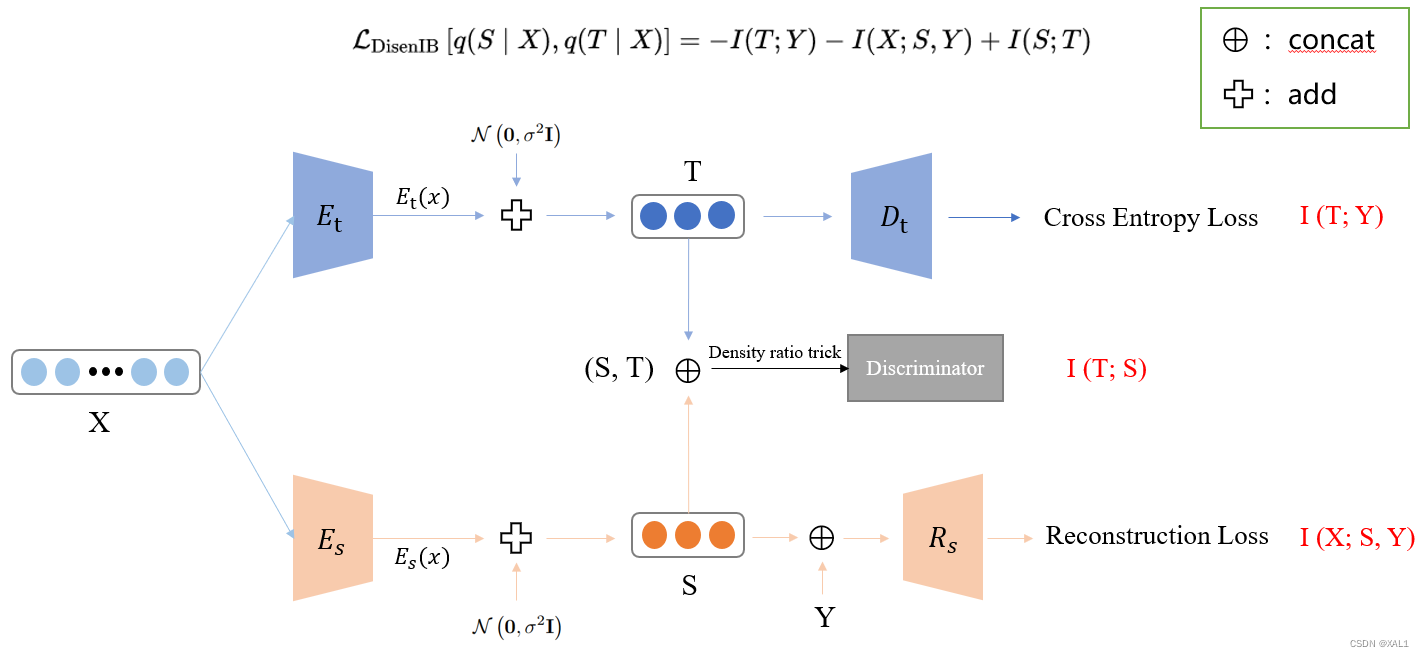
伪代码如下: