目录
- 1.题目
- 2.思路
- 3.代码实现(Java)
1.题目
给你一棵由 n 个顶点组成的无向树,顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下:
- 在一秒内,青蛙从它所在的当前顶点跳到另一个未访问过的顶点(如果它们直接相连)。
- 青蛙无法跳回已经访问过的顶点。
- 如果青蛙可以跳到多个不同顶点,那么它跳到其中任意一个顶点上的机率都相同。
- 如果青蛙不能跳到任何未访问过的顶点上,那么它每次跳跃都会停留在原地。无向树的边用数组 edges 描述,其中 edges[i] = [ai, bi] 意味着存在一条直接连通 ai 和 bi 两个顶点的边。
返回青蛙在 t 秒后位于目标顶点 target 上的概率。与实际答案相差不超过 10-5 的结果将被视为正确答案。
示例 1:
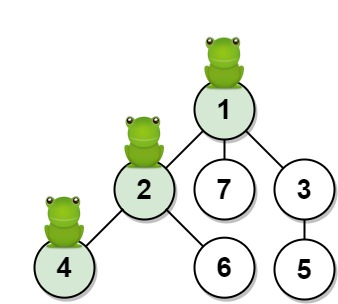
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出:0.16666666666666666
解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,第 1 秒 有 1/3 的概率跳到顶点 2 ,然后第 2 秒 有 1/2 的概率跳到顶点 4,因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。
示例 2:
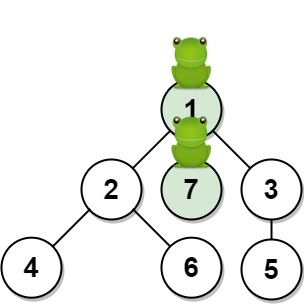
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
输出:0.3333333333333333
解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。
提示:
1 <= n <= 100
edges.length == n - 1
edges[i].length == 2
1 <= ai, bi <= n
1 <= t <= 50
1 <= target <= n
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/frog-position-after-t-seconds
2.思路
(1)DFS
思路参考本题官方题解。
- 为了方便我们对图进行搜索,先根据 edges 构造出无向树的邻接表
graph,并且定义数组visited来标记节点是否已经被遍历过 - 然后使用 dfs 来进行深度遍历,其中,dfs 的参数包括:
- 邻接表
graph、数组visited; - 当前遍历的顶点序号 i、剩余时间 restTime,以及目标顶点编号 target;
- 邻接表
- 每次遍历一个节点时候:
- 如果当前节点没有后续节点,或者剩余时间为 0,则不能继续搜索;此时当前节点是 target,返回概率 1.0,否则返回概率为 0.0
- 如果有后续节点,并且剩余时间不为 0,则继续深度优先搜索,如果有子节点返回概率 p > 0,说明已经找到了节点 target,又因为跳到任意一个后续子节点上的机率都相同, 我们返回概率 p 除以后续节点个数的商,作为最后的结果。
3.代码实现(Java)
//思路1————DFS
class Solution {
public double frogPosition(int n, int[][] edges, int t, int target) {
//创建邻接表 graph
List<Integer>[] graph = new ArrayList[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = new ArrayList<>();
}
for (int[] edge : edges) {
graph[edge[0]].add(edge[1]);
graph[edge[1]].add(edge[0]);
}
boolean[] visited = new boolean[n + 1];
return dfs(graph, visited, 1, t, target);
}
//返回从节点 i 开始,在剩余时间为 restTime 秒后位于目标节点 target 的概率
private double dfs(List<Integer>[] graph, boolean[] visited, int i, int restTime, int target) {
int next = (i == 1) ? graph[i].size() : graph[i].size() - 1;
//剩余时间不足或者当前节点没有后续节点
if (restTime == 0 || next == 0) {
return i == target ? 1.0 : 0.0;
}
visited[i] = true;
double res = 0.0;
for (int j : graph[i]) {
if (!visited[j]) {
res += dfs(graph, visited, j, restTime - 1, target);
}
}
return res / next;
}
}