目录
围栏木桩
某农场有一个由按编号排列的根木桩构成的首尾不相连的围栏。现要在这个围栏中选取一些木桩,按照原有的编号次序排列之后,这些木桩高度成一个升序序列。
大厨小码哥
附庸的附庸
最长子段和
旅费
纸带
暧昧团
上楼梯
上楼梯2
采蜜

围栏木桩
某农场有一个由按编号排列的根木桩构成的首尾不相连的围栏。现要在这个围栏中选取一些木桩,按照原有的编号次序排列之后,这些木桩高度成一个升序序列。
难度:黄金
0时间限制:1秒
巴占用内存:128M
某农场有一个由按编号排列的根木桩构成的首尾不相连的围栏。现要在这个围栏中
选取一些木桩,按照原有的编号次序排列之后,这些木桩高度成一个升序序列。所谓
的升序序列就是序列中的任何一个数都不小于它之前的任何一个数。试编写程序从这
个围栏中选取合适的木桩使得选出的木桩个数t最大,并求出选取出t根木桩的方案
总数c。
格式
输入格式:文件中的第一行只有一个数m,表明随后有m个问题的描述信息。
每个问题的描述信息格式为n,h1,h2,hg,,hn(其中h:(i=
1,2,3,..,n)表示第i根木桩的高度)。
输出格式:依次输出每个问题中t和c的解,每行输出一个问题的解。
//
// Created by abner on 2023/5/24.
//
#include <bits/stdc++.h>
using namespace std;
const int N = 27;
int n,m,h[N],dp[N],f[N],ans_t,ans_c;
int main(){
cin >>m;
while (m--){
ans_t = ans_c = 0;
memset(h,0,sizeof(h));
memset(dp,0,sizeof(dp));
memset(f,0,sizeof(f));
cin >> n;
for(int i=1;i<=n;++i){
cin >> h[i];
dp[i]=f[i]=1;
}
for(int i=2;i<=n;++i)
for (int j=i-1;j;--j)
if(h[j]<=h[i]){
if (dp[j]+1>dp[i]) {
dp[i] = dp[j] + 1;
f[i] = f[j];
} else if (dp[j]+1 == dp[i])
f[i]++;
}
for (int i = 1;i<=n;++i)
ans_t = max(ans_t,dp[i]);
for(int i=1;i<=n;++i)
if(dp[i]==ans_t)
ans_c +=f[i];
cout <<ans_t <<' '<<ans_c <<endl;
}
return 0;
}
大厨小码哥
难度:黄金
时间限制:1秒
巴占用内存:128M
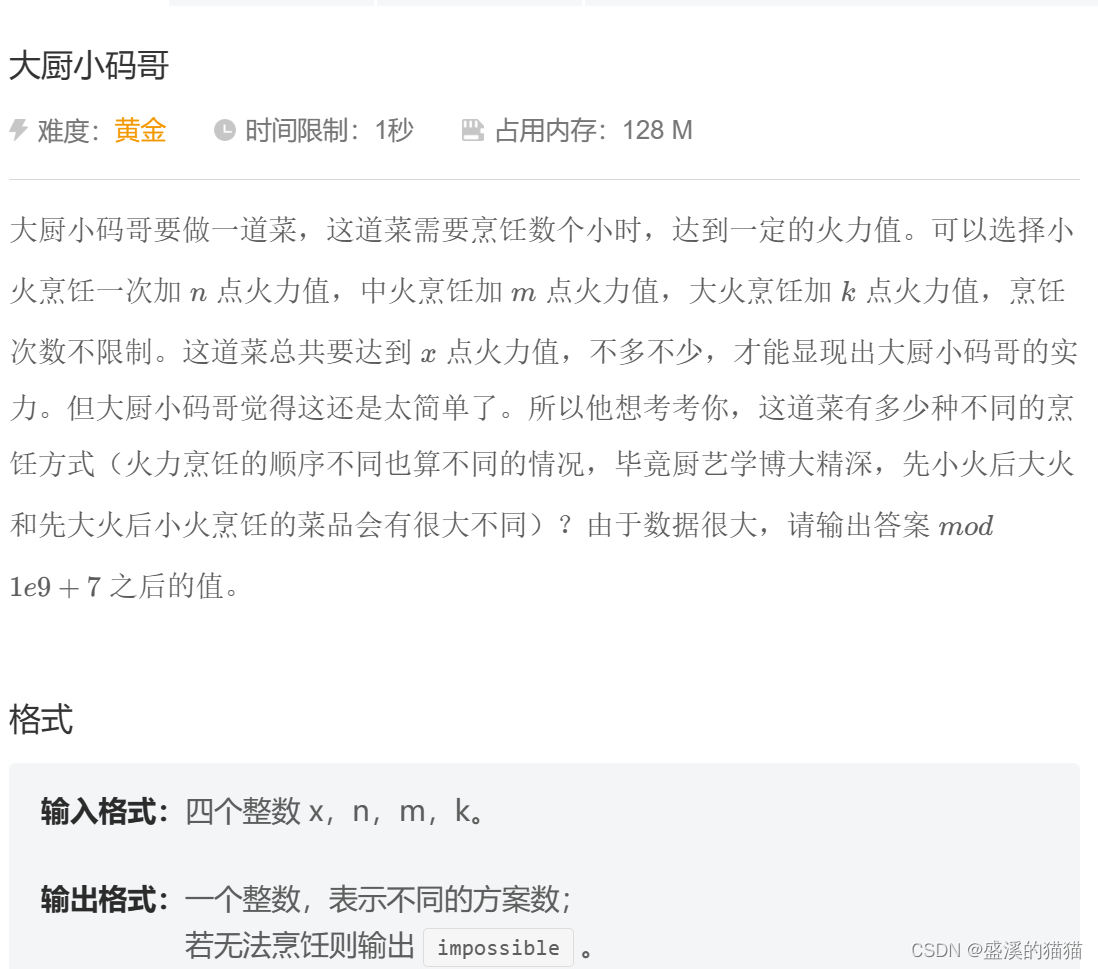
大厨小码哥要做一道菜,这道菜需要烹饪数个小时,达到一定的火力值。可以选择小
火烹饪一次加点火力值,中火烹饪加m点火力值,大火烹饪加k点火力值,烹饪
次数不限制。这道菜总共要达到x点火力值,不多不少,才能显现出大厨小码哥的实
力。但大厨小码哥觉得这还是太简单了。所以他想考考你,这道菜有多少种不同的烹
饪方式(火力烹饪的顺序不同也算不同的情况,毕竟厨艺学博大精深,先小火后大火
和先大火后小火烹饪的菜品会有很大不同)?由于数据很大,请输出答案m0d
1e9+7之后的值。
格式
输入格式:四个整数X,n,m,k。
输出格式:一个整数,表示不同的方案数;
//
// Created by abner on 2023/5/24.
//
#include <bits/stdc++.h>
using namespace std;
#define mem(a) memset(a, 0, sizeof(a))
#define dbg(x) cout << #x << " = " << x << endl
#define fi(i, l, r) for (int i = l; i < r; i++)
#define cd(a) scanf("%d", &a)
typedef long long ll;
ll dp[1010] = {1, 0};
const ll mod = 1e9 + 7;
int main() {
int x;
int val[3];
cin >> x;
for (int i = 0; i < 3; i++) {
cin >> val[i];
}
for (int i = 1; i <= x; i++) {
for (int j = 0; j < 3; j++) {
if (i - val[j] >= 0) {
dp[i] += dp[i - val[j]];
dp[i] %= mod;
}
}
}
if (dp[x]) {
cout << dp[x] << endl;
}
else {
puts("impossible");
}
return 0;
}

附庸的附庸
难度:黄金
0时间限制:1秒
巴占用内存:128M
蒙德城的旧贵族们存在着附庸的关系。欧洲有一位伟人说过,我的附庸的附庸不是我
的附庸。尽管如此,他们还是存在着隐性的自上而下的关系,属于同一个利益集团。
所以,在蒙德城,附庸的附庸也是附庸。也就是说,如果两个附庸都能追溯到同一个
贵族,他们也存在附庸关系(仅仅是蒙德人这样认为)蒙德城人口众多,现在小码哥
把各人的关系都梳理了出来交给了你,并想让你告诉他,某两个人存不存在附庸关系
(按照蒙德人的观念)。
格式
输入格式:第一行一个整数n,表示n个关系;
接下来n行,每行两个数a,b,表示b是a的附庸;
下一行一个整数q,表示询问次数;
接下来g行,每行两个数a,b,询问a和b是否存在附庸关系。
//
// Created by abner on 2023/5/24.
//
#include <bits/stdc++.h>
using namespace std;
const int N = 2e4 +7;
int fa[N],n,q,a,b;
void init(int n) {
for (int i = 1; i <= n; i++)
fa[i] = i;
}
int find(int x)//查找
{ return x == fa[x] ? x : (fa[x] = find(fa[x]));//路径压缩
}
int main(){
cin >>n;
init(N);
while (n--){
cin >>a >>b;
fa[b] = a;}
cin >>q;
while (q--){
cin >>a >>b;
if (find(a)==find(b))
cout <<"1"<<endl;
else
cout <<"0"<<endl;
}
return 0;
}
最长子段和
号难度:钻石
0时间限制:1秒
巴占用内存:128M
给出一个长度为n的序列α,选出其中连续且非空的一段使得这段和最大。
格式
输入格式:第一行是一个整数,表示序列的长度;
第二行有n个整数,第i个整数表示序列的第i个数字a:。
输出格式:输出一行一个整数表示答案。
样例1
输入:7
复制
2-43-12-43
输出:4
复制
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1000010;
int n, a[N], dp[N], res = -9999999;
int main(){
cin >> n;
for (int i = 1 ; i <= n ; i ++ ) cin >> a[i];
for (int i = 1 ; i <= n ; i ++ ){
dp[i] = max(dp[i - 1] + a[i], a[i]);//状态转移方程->选or不选a[i]
res = max(res, dp[i]);
}
cout << res;
return 0;
}
旅费
难度:黄金
0时间限制:1秒
巴占用内存:128M
提瓦特大陆上有个贫穷的占星术士小码哥,他要从蒙德去往璃月,两个地方相隔很
远,所以要搭乘车队。但是搭乘车队需要金币,而小码哥没有太多金币,幸运的是,
车队在这一路上有个停靠点,每两个停靠点之间所需要的金币数不一样,如果能选
择好的话说不定能省点钱。于是小码哥找来了每个站点之间所需的路费,请你帮他找
出他完成这一旅途所需要的最少的旅费。
格式
输入格式:第一行输入一个数,表示马车中间停靠的站点数;
接下来一个+1行的半矩阵,表示从蒙德开始,每个站点到接下来
每个站点所需要的金币数。
输出格式:输出一行一个正整数,表示完成这一旅途所需要的最少的旅费(金
币数)。
//
// Created by abner on 2023/5/24.
//
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 +7;
int a[N][N],dp [N],n;
int main(){
cin >>n;
n++;
for (int i=0;i<n;i++){
for (int j =i+1;j <=n;j++)
cin >>a[i][j];
dp[i]= 0x3f3f3f3f;
}
for(int i=n-1;i>=0;i--)
for (int j=i+1;j <=n;j++)
dp[i] =min(dp[i],a[i][j]+dp[j]);
cout <<dp[0];
return 0;
}
纸带
难度:钻石
0时间限制:6秒
巴占用内存:128M
小码哥有一张1×n的纸带,由n个格子组成。初始有一个点在n号格子(即
左数第n个)中。
假设现在这个点在x(x>1)号格子,每次小码哥可以对这个点进行如下操作中的一
种:
减法。选择一个[1,x一1中的正整数y,将点移动到x一y号格子中。
除法。选择一个[2,中的正整数之,将点移动到L」号格子中。
当点在1号格子中时无法移动,操作结束。
求将点从号格子移到1号格子的方案数,答案对给定的模数取模。
两个方案不同当且仅当有一步选择的操作或选择的数不同。
//
// Created by abner on 2023/5/24.
//
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=4e6 +5;
int n,mod;
ll dp[N],sum[N];
int main(){
cin >>n >>mod;
dp[n]=sum[n]=1;
for (int i =n-1;i>=1;i--){
dp[i] = sum[i+1];
for (int j=2;j*i<=n;j++) {
int r = min(n, i * j + j - 1);
dp[i] = (dp[i] + sum[i * j] - sum[r + 1]) % mod;
}
sum[i] = (sum[i + 1]+ dp[i])%mod;
}
cout << dp[1];
return 0;
}
暧昧团
难度:黄金
©时间限制:1秒
巴占用内存:128M
小码哥正在整理NPU的学生信息。现在到了关键的一步:存储cp信息。
因为众所周知情网很乱,所以可能一个人和多个人暖味,并且不分性别,而且有可能
自己和自己暖味。
同时一对暖昧关系可能会由于大意等原因多次记录。
现在我们知道n个人,并且有m个暖味关系。
现在我们对暖昧团进行定义:一个人所有和他有直接暖昧关系以及间接暖昧关系的集
合。
比如1与2暖昧,2与3暧昧,3与4暖昧,5与3暖昧,6与2暖昧,那么
{1,2,3,4,5,6},{2,3},{1,4,5,6},{空集合}就均属于暧昧团,其中,
{1,2,3,4,5,6就是极大暖昧团。
现在小码哥告诉你一个人名的编号x,让你回答与x所处极大暖味团的大小。
#include<bits/stdc++.h>
using namespace std;
int n,m,a,b,f[100005],sz[100005];
int find(int x){
return x==f[x]?x:f[x]=find(f[x]);
}
int main( )
{
cin>>n>>m;
for(int i=1;i<=n;i++) sz[i]=1,f[i]=i;
while(m--){
cin>>a>>b;
int fa=find(a),fb=find(b);
if(fa!=fb){
f[fa]=fb;
sz[fb]+=sz[fa];
}
}
cin>>a;cout<<sz[find(a)];
return 0;
}
上楼梯
难度:黄金
时间限制:1秒
巴占用内存:128M
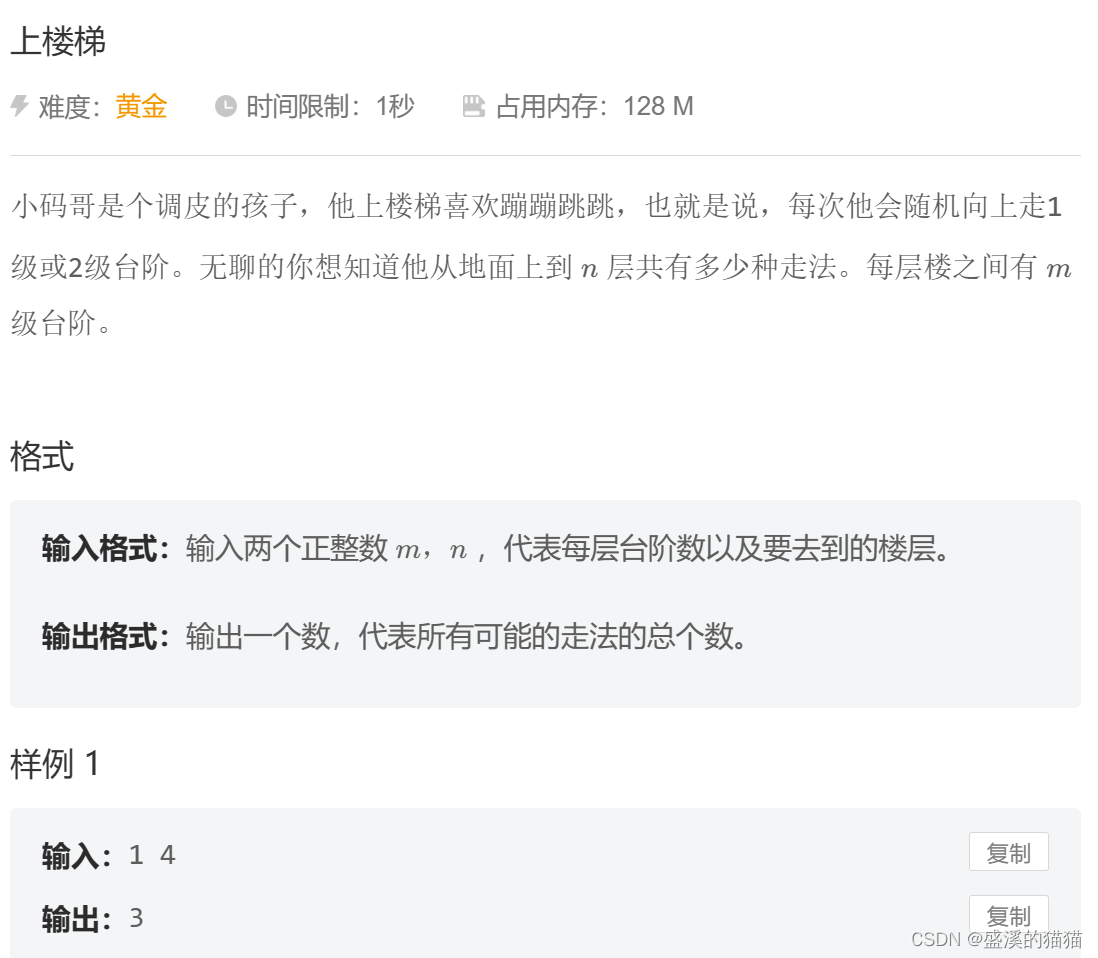
小码哥是个调皮的孩子,他上楼梯喜欢蹦蹦跳跳,也就是说,每次他会随机向上走1
级或2级台阶。无聊的你想知道他从地面上到n层共有多少种走法。每层楼之间有m
级台阶。
格式
输入格式:输入两个正整数m,n,代表每层台阶数以及要去到的楼层。
输出格式:输出一个数,代表所有可能的走法的总个数。
样例1
输入:14
复制
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[100005]={
0};
int main( )
{
int n,m;
cin>>m>>n;
dp[0] = 0;
dp[1] = 1,dp[2] = 2;
for(int i=3;i<=m*(n-1);i++) dp[i] = dp[i-1]+dp[i-2];
cout<<dp[m*(n-1)]<<'\n';
return 0;
}
上楼梯2
难度:黄金
时间限制:1秒
巴占用内存:128M
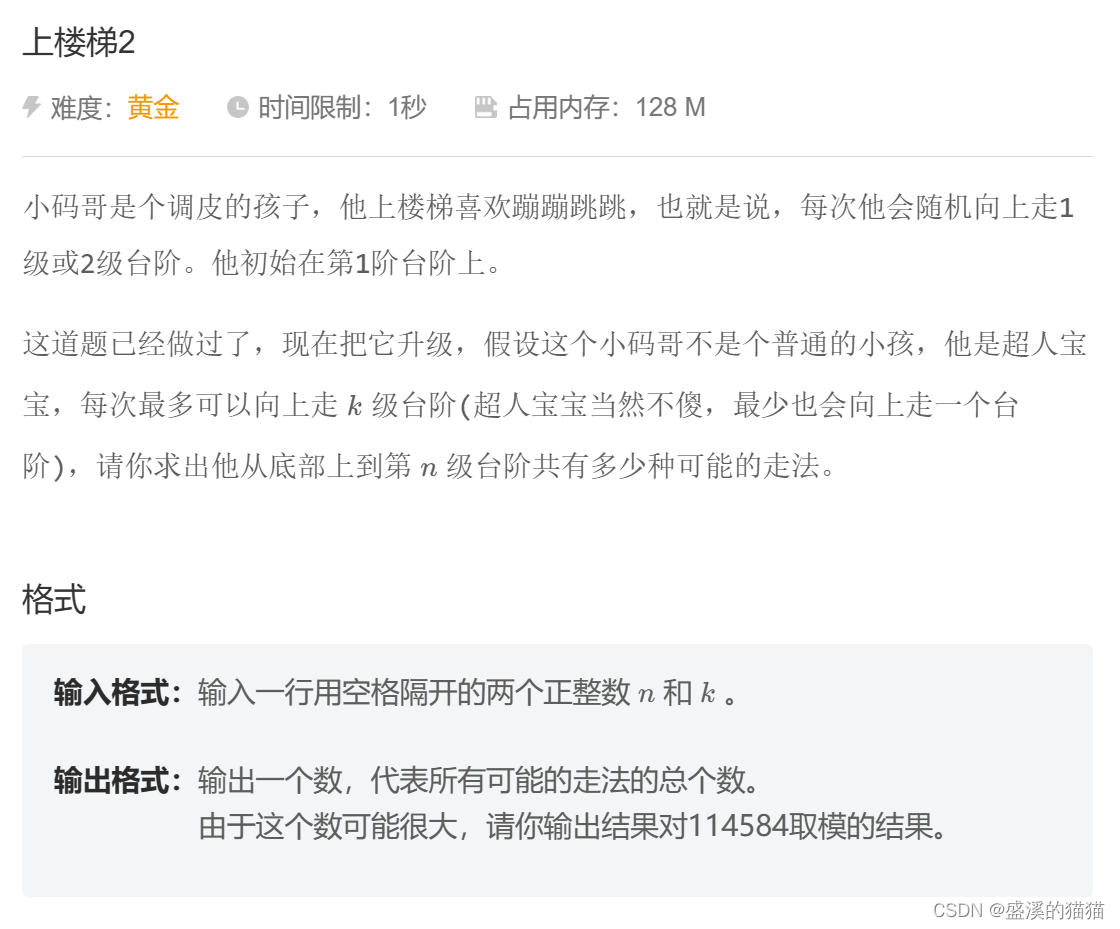
小码哥是个调皮的孩子,他上楼梯喜欢蹦蹦跳跳,也就是说,每次他会随机向上走1
级或2级台阶。他初始在第1阶台阶上。
这道题已经做过了,现在把它升级,假设这个小码哥不是个普通的小孩,他是超人宝
宝,每次最多可以向上走k级台阶(超人宝宝当然不傻,最少也会向上走一个台
阶),请你求出他从底部上到第级台阶共有多少种可能的走法。
格式
输入格式:输入一行用空格隔开的两个正整数和k。
输出格式:输出一个数,代表所有可能的走法的总个数。
由于这个数可能很大,请你输出结果对114584取模的结果。
def main():
#code here
n,k=map(int,input().split())
f = [0 for i in range(n+1)]
f[0]=1
f[1]=1
for i in range(2,n+1):
for j in range(1,min(k+1,i+1)):
f[i]+=f[i-j]
f[i]%=114584
print(f[n])
if __name__ == '__main__':
main();
采蜜
难度:黄金
0时间限制:1秒
巴占用内存:128M
现在有n个蜂巢,每一个蜂窝都对应了一个蜂蜜值s:。
小码哥发现:有一些峰窝相互联结,使得他们可以共享蜂蜜值,即该蜂巢的蜂蜜值变
为:它和它连接(直接连接或间接连接)的蜂巢的蜂蜜值的和。
现在小码哥想要查询一下一些蜂巢的蜂蜜值。
格式
输入格式:第一行有两个数
n(蜂巢的数量)
、
m(操作的数量)
第二行有n个数字(s1,·,sn):分别表示了每一个蜂巢的蜂蜜
值。
随后有m行:第一个数字如果是1,则后面还有两个数字a,b
表示此次发现蜂巢α和b是相连的。第一个数字如果是2,则
后面只有一个数字c,表示查询所有与蜂巢℃相连的蜂巢(包括自
己)的总蜂蜜值。
#include<cstdio>
#define maxn 100005
using namespace std;
int n,m,a[maxn],fa[maxn];
inline int get(int x){
if (x==fa[x]) return x;
return fa[x]=get(fa[x]);
}
int main(){
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++) scanf("%d",&a[i]),fa[i]=i;
while (m--){
int f=0;
scanf("%d",&f);
if (f==1){
int x,y;
scanf("%d%d",&x,&y);
int fx=get(x),fy=get(y);
if (fx!=fy){
fa[fy]=fx;
a[fx]+=a[fy];
}
}else{
int x;scanf("%d",&x);
printf("%d\n",a[get(x)]);
}
}
return 0;
}