目录
- 前言
- 实验内容
- 实验流程
- 实验过程
- 实验分析
- 伪代码
- 代码实现
- 分析算法复杂度
- 用例测试
- 总结
前言
动态规划是一种解决复杂问题的方法,它将一个问题分解为若干个子问题,然后从最简单的子问题开始求解,逐步推导出更复杂的子问题的解,最终得到原问题的最优解。动态规划的关键是找到子问题之间的递推关系,以及确定合适的边界条件和初始值。
数塔问题是一个经典的动态规划问题,它描述了一个由数字组成的三角形结构,要求从顶部开始向下走,每次只能走到相邻的位置,最终到达底部,使得经过的数字之和最大。数塔问题可以用一个二维数组来表示,其中第i行有i个元素,表示第i层的数字。例如:
9
12 15
10 6 8
2 18 9 5
16 12 18 10 8
数塔问题的一个可能的最优路径是:9 -> 15 -> 8 -> 9 -> 18,其和为59。
实验内容
给出一个数塔,从该数塔的顶层出发,在每一个节点可以选择向左走或向右走,一直走到该数塔的最底层,找出一条路径,使得路径上的数值和最大,输出最大数值及其路径,输出时要求有文字说明。请任选一种语言编写程序实现上述算法,并分析其算法复杂度。
实验流程
根据实验内容设计算法伪代码进行算法描述;
利用C++/C/Java等编程语言对算法伪代码进行工程化实现;
输入测试用例对算法进行验证;
列出算法时间复杂度模型并与计算机运行统计时间进行对比分析。
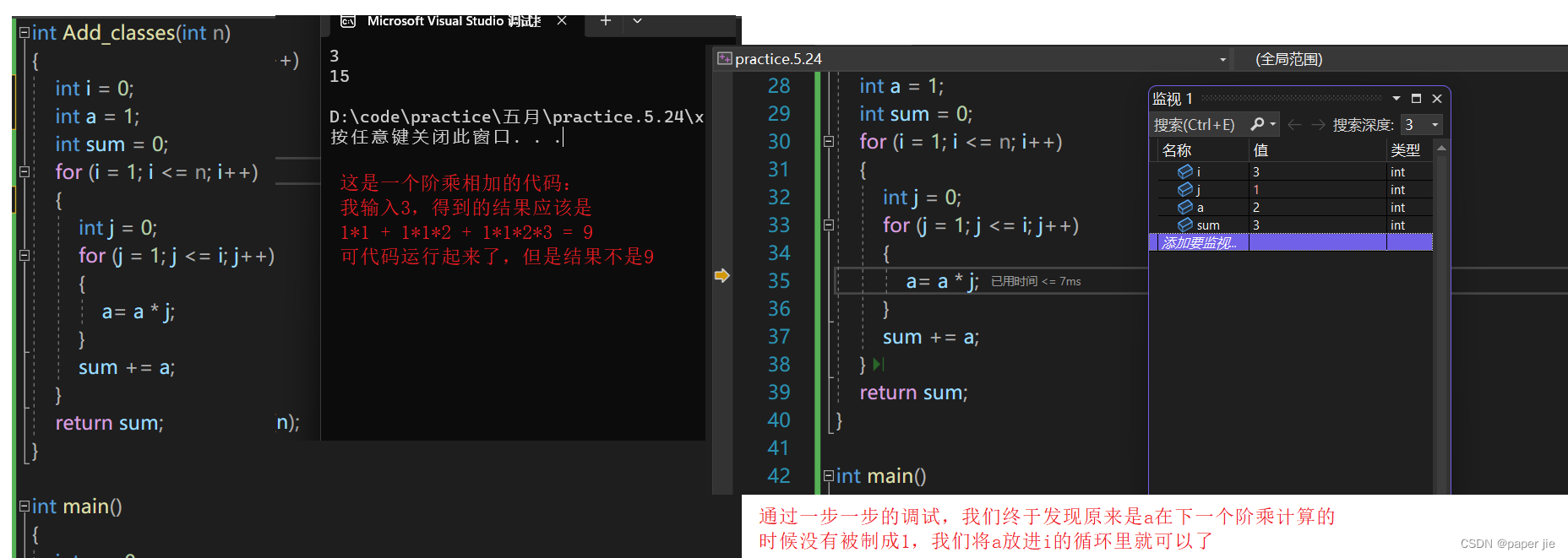
实验过程
实验分析
这个问题是一个典型的动态规划问题,动态规划的基本思想是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。动态规划通常需要保存已解决的子问题的答案,以避免重复计算,节省时间。
对于数塔问题,我们可以从下往上逐层计算每个节点到底层的最大路径和,并记录下每个节点选择的方向。最后从顶层开始根据方向输出路径即可。
例如,给定一个数塔如下:
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
我们可以用一个二维数组a来存储数塔中的数字,用另一个二维数组f来存储每个节点到底层的最大路径和,用另一个二维数组p来存储每个节点选择的方向(0表示左,1表示右)。初始化时,f的最后一行就是a的最后一行,p可以任意初始化。
然后我们从倒数第二行开始,逐层向上计算f和p。对于每个节点a[i][j],我们比较它下面两个节点f[i+1][j]和f[i+1][j+1]的大小,选择较大者作为它到底层的最大路径和,并记录下选择的方向。具体地,有如下状态转移方程:
f[i][j] = max(f[i+1][j], f[i+1][j+1]) + a[i][j]
p[i][j] = f[i+1][j] > f[i+1][j+1] ? 0 : 1
复制
当我们计算完所有的f和p后,f[0][0]就是数塔顶层到底层的最大路径和。我们可以从顶层开始根据p输出路径。具体地,我们用两个变量i和j表示当前节点的位置,初始为0和0。然后我们输出a[i][j],并根据p[i][j]更新i和j(如果p[i][j]为0,则i=i+1,j=j;如果p[i][j]为1,则i=i+1,j=j+1)。重复这个过程直到i等于数塔的高度。
例如,对于上面给定的数塔,计算完f和p后得到如下结果:
f:
30
23 21
20 13 10
7 12 10 10
4 5 2 6 5
p:
1
0 1
0 0 0
0 0 0 0
则最大路径和为30,路径为7->3->8->7->5。
伪代码
// Define a constant for the maximum height of the tower
constant MAXN = 100
// Declare a two-dimensional array to store the numbers in the tower
array a[MAXN][MAXN]
// Declare a two-dimensional array to store the maximum path sum from each node to the bottom
array f[MAXN][MAXN]
// Declare a two-dimensional array to store the direction of each node (0 for left, 1 for right)
array p[MAXN][MAXN]
// Define the main program
function main()
// Declare an integer variable to store the height of the tower
integer n
// Input the height from the user
input n
// Input the numbers in the tower from the user
for i from 0 to n-1 // Loop through each row
for j from 0 to i // Loop through each column
input a[i][j]
// Initialize f and p
for j from 0 to n-1 // Loop through the last row
f[n-1][j] = a[n-1][j] // The last row of f is the same as the last row of a
p[n-1][j] = -1 // The last row of p has no direction to choose
// Compute f and p from bottom to top
for i from n-2 to 0 // Loop through each row except the last one in reverse order
for j from 0 to i // Loop through each column
if f[i+1][j] > f[i+1][j+1] // If the left child is larger than the right child
f[i][j] = f[i+1][j] + a[i][j] // Choose the left child as the maximum path sum and add the current node value
p[i][j] = 0 // Record the direction as left
else // Otherwise
f[i][j] = f[i+1][j+1] + a[i][j] // Choose the right child as the maximum path sum and add the current node value
p[i][j] = 1 // Record the direction as right
// Output the maximum path sum and its path
print "最大路径和为:" + f[0][0] // The maximum path sum is f[0][0]
print "路径为:"
i = 0, j = 0 // The current node position (starting from the top)
while i < n // Loop until reaching the bottom row
print a[i][j] + " " // Output the current node value
if p[i][j] == -1 // If there is no direction to choose, break the loop (reached the bottom row)
break
if p[i][j] == 0 // If the direction is left, update the position to the next row and same column
i = i + 1
else // If the direction is right, update the position to the next row and right column
i = i + 1
j = j + 1
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define MAXN 100 // 数塔最大高度
int a[MAXN][MAXN]; // 存储数塔中的数字
int f[MAXN][MAXN]; // 存储每个节点到底层的最大路径和
int p[MAXN][MAXN]; // 存储每个节点选择的方向(0表示左,1表示右)
int main() {
int n; // 数塔高度
scanf("%d", &n); // 输入高度
// 输入数塔中的数字
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) {
scanf("%d", &a[i][j]);
}
}
// 初始化f和p
for (int j = 0; j < n; j++) {
f[n-1][j] = a[n-1][j]; // 最后一行就是a的最后一行
p[n-1][j] = -1; // 最后一行没有方向可选
}
// 自底向上计算f和p
for (int i = n-2; i >= 0; i--) { // 倒数第二行开始往上
for (int j = 0; j <= i; j++) { // 每行有i+1个节点
if (f[i+1][j] > f[i+1][j+1]) { // 如果左边大于右边
f[i][j] = f[i+1][j] + a[i][j]; // 则选择左边作为最大路径和,并加上当前节点值
p[i][j] = 0; // 记录方向为左
} else { // 否则选择右边作为最大路径和,并加上当前节点值
f[i][j] = f[i+1][j+1] + a[i][j];
p[i][j] = 1; // 记录方向为右
}
}
}
// 输出最大路径和及其路径
printf("最大路径和为:%d\n", f[0][0]); // 最大路径和就是f[0][0]
printf("路径为:");
int i = 0, j = 0; // 当前节点位置(从顶层开始)
while (i < n) { // 直到到达底层结束循环
printf("%d ", a[i][j]); // 输出当前节点值
if (p[i][j] == -1) break; // 如果没有方向可选,则结束循环(已经到达底层)
if (p[i][j] == 0) { // 如果方向为左,则更新位置为下一行同一列
i++;
} else { // 如果方向为右,则更新位置为下一行右一列
i++;
j++;
}
}
printf("\n");
return 0;
}
分析算法复杂度
时间复杂度:由于需要遍历整个数塔两次(一次输入数字,一次计算f和p),所以时间复杂度为O(n^2),其中n为数塔高度。
空间复杂度:由于需要使用三个二维数组来存储数字、最大路径和、方向信息,所以空间复杂度也为O(n^2),其中n为数塔高度。
用例测试
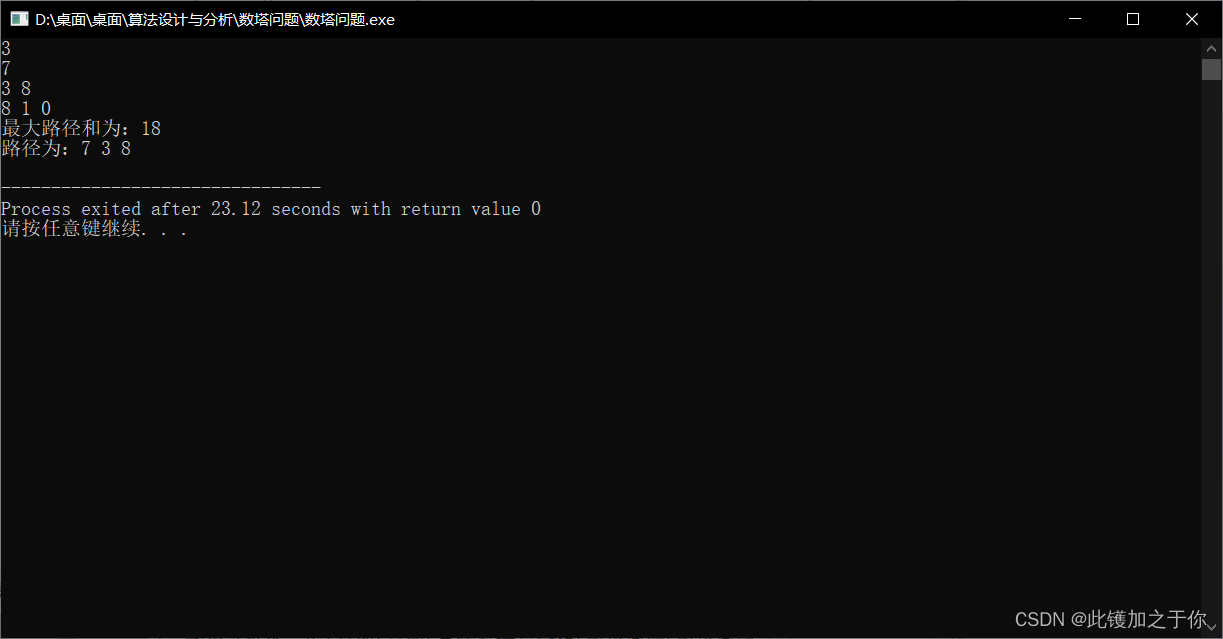
总结
本实验的目的是掌握动态规划的基本思想和方法,以及如何应用动态规划解决数塔问题。数塔问题是一个经典的动态规划问题,给定一个由n层数字组成的三角形,从顶层出发,在每一层可以选择左边或右边的数字,一直走到底层,求出所经过的数字之和的最大值。本实验采用自底向上的方法,从底层开始,计算每个位置到底层的最大值,并存储在一个二维数组中,最后得到顶层到底层的最大值。本实验还要求输出最大值对应的路径,即所选择的数字序列。为了实现这一功能,需要在计算过程中记录每个位置选择的方向,并在计算完成后从顶层开始回溯,输出所选择的数字。
本实验的难点在于理解动态规划的原理和过程,以及编写正确和高效的代码。动态规划是一种将复杂问题分解为子问题,并利用子问题之间的关系和重复性,避免重复计算,从而提高效率的方法。动态规划适用于具有最优子结构和重叠子问题的问题。最优子结构指的是原问题的最优解可以由子问题的最优解构成,重叠子问题指的是在求解过程中会多次遇到相同的子问题。数塔问题满足这两个条件,因为每个位置到底层的最大值只取决于它下面一层相邻两个位置的最大值,而且在计算过程中会多次计算同一个位置到底层的最大值。因此,可以用动态规划来解决数塔问题。
本实验还需要注意代码的编写规范和风格,以及程序的可读性和可维护性。代码应该遵循统一和清晰的命名规则,使用适当的注释和缩进,避免冗余和无用的代码,使用合理的数据结构和算法,处理好边界情况和异常情况等。程序应该具有良好的模块化和封装性,将不同功能分离为不同函数或类,并提供清晰和完整的接口和文档。