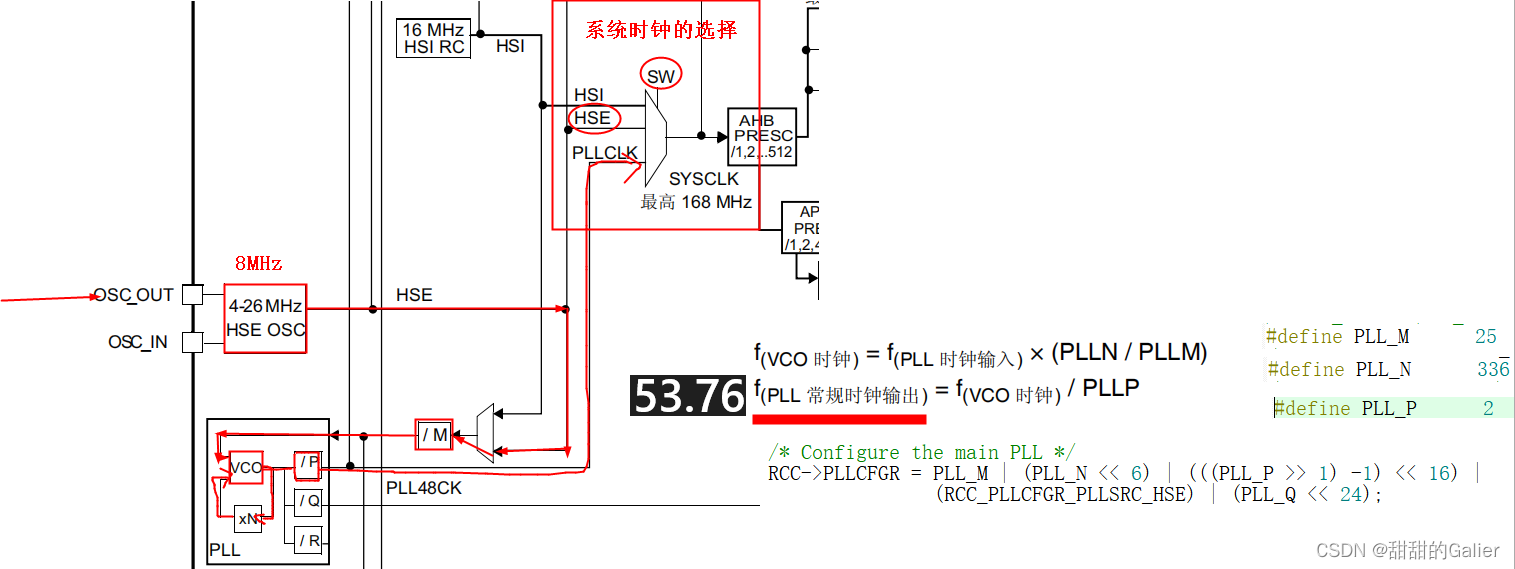
仅作自己笔记用

1，FFT函数调用基础知识

     采样得到的数字信号，就可以做FFT变换了。N个采样点，经过FFT之后，就可以得到N个点的FFT结果。为了方便进行FFT运算，通常N取2的整数次方。

假设采样频率为Fs，信号频率F，采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。而第一个点就是直流分量，它的模值就是直流分量的N倍。而每个点的相位呢，就是在该频率下的信号的相位。第一个点表示直流分量（即0Hz），而最后一个点N的再下一个点（实际上这个点是不存在的，这里是假设的第N+1个点，也可以看做是将第一个点分做两半分，另一半移到最后）则表示采样频率Fs，这中间被N-1个点平均分成N等份，每个点的频率依次增加。例如某点n所表示的频率为：Fn=(n-1)*Fs/N。由上面的公式可以看出，Fn所能分辨到频率为为Fs/N，如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。1024Hz的采样率采样1024点，刚好是1秒，也就是说，采样1秒时间的信号并做FFT，则结果可以分析到1Hz，如果采样2秒时间的信号并做FFT，则结果可以分析到0.5Hz。如果要提高频率分辨力，则必须增加采样点数，也即采样时间。频率分辨率和采样时间是倒数关系。

假设FFT之后某点n用复数a+bi表示，那么这个复数的模就是An=根号a*a+b*b，相位就是Pn=atan2(b,a)。根据以上的结果，就可以计算出n点（n≠1，且n<=N/2）对应的信号的表达式为：An/(N/2)*cos(2*pi*Fn*t+Pn)，即2*An/N*cos(2*pi*Fn*t+Pn)。
对于n=1点的信号，是直流分量，幅度即为A1/N。由于FFT结果的对称性，通常我们只使用前半部分的结果，即小于采样频率一半的结果。

2，DSP库函数。

FFT 算法的实质是把一长序列的 DFT 计算分割为较短序列的 DFT 计算，对于基2算法而言，是把序列每次一分为二，最后分割成两点 DFT，也可以采用别的分割法，每次一分为四，八等，就得到了基4，基8等算法；基数越大，一般速度越快。

stm32的DSP库中

基2函数：arm_cfft_radix2_f32();

基4函数：arm_cfft_radix4_f32();

不过，新版库函数，可以使用混合基函数，这样更方便，速度更快。

arm_cfft_f32();

f32是单精度；f64是双精度；

以混合基函数函数介绍，从下面代码中可以看出，混合基将基2，基4，基8等放在一起了。

/**
* @details
* @brief       Processing function for the floating-point complex FFT.
* @param[in]      *S    points to an instance of the floating-point CFFT structure.
* @param[in, out] *p1   points to the complex data buffer of size <code>2*fftLen</code>. Processing occurs in-place.
* @param[in]     ifftFlag       flag that selects forward (ifftFlag=0) or inverse (ifftFlag=1) transform.
* @param[in]     bitReverseFlag flag that enables (bitReverseFlag=1) or disables (bitReverseFlag=0) bit reversal of output.
* @return none.
*/

void arm_cfft_f32(
    const arm_cfft_instance_f32 * S,
    float32_t * p1,
    uint8_t ifftFlag,
    uint8_t bitReverseFlag)
{
    uint32_t  L = S->fftLen, l;
    float32_t invL, * pSrc;

    if (ifftFlag == 1U)
    {
        /*  Conjugate input data  */
        pSrc = p1 + 1;
        for(l=0; l<L; l++)
        {
            *pSrc = -*pSrc;
            pSrc += 2;
        }
    }

    switch (L)
    {
    case 16:
    case 128:
    case 1024:
        arm_cfft_radix8by2_f32  ( (arm_cfft_instance_f32 *) S, p1);
        break;
    case 32:
    case 256:
    case 2048:
        arm_cfft_radix8by4_f32  ( (arm_cfft_instance_f32 *) S, p1);
        break;
    case 64:
    case 512:
    case 4096:
        arm_radix8_butterfly_f32( p1, L, (float32_t *) S->pTwiddle, 1);
        break;
    }

    if ( bitReverseFlag )
        arm_bitreversal_32((uint32_t*)p1,S->bitRevLength,S->pBitRevTable);

    if (ifftFlag == 1U)
    {
        invL = 1.0f/(float32_t)L;
        /*  Conjugate and scale output data */
        pSrc = p1;
        for(l=0; l<L; l++)
        {
            *pSrc++ *=   invL ;
            *pSrc  = -(*pSrc) * invL;
            pSrc++;
        }
    }
}

使用举例

arm_cfft_f32(&arm_cfft_sR_f32_len1024,fft_inputbuf,ifftFlag,doBitReverse);

参数1：是一个arm_cfft_instance_f32类型的结构体变量，包含数据个数等信息；

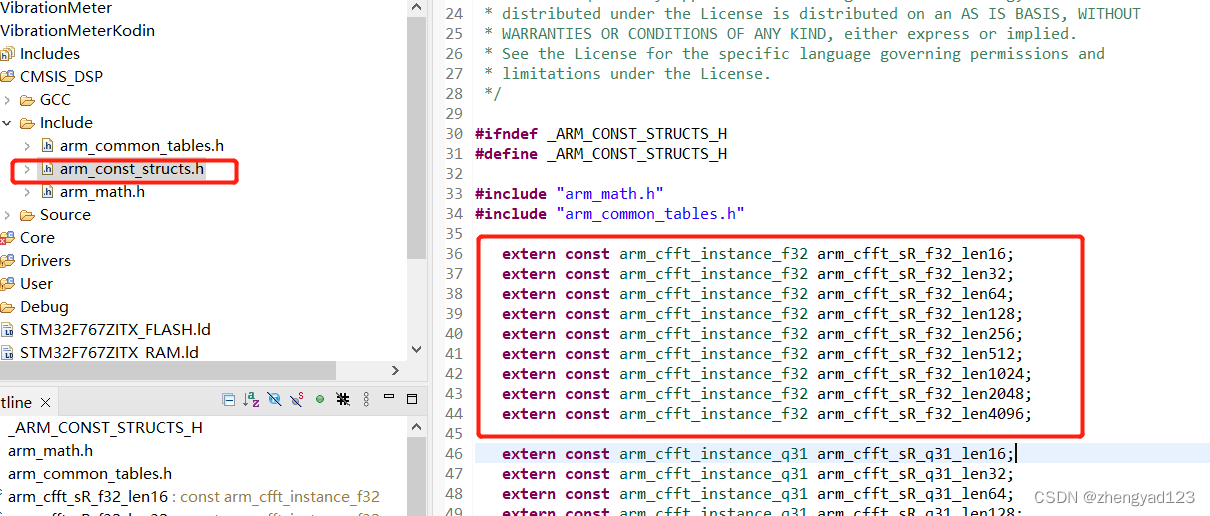
 参数2：数组，要变换的数据。要变换的数据是一个复数，前面i是实部，后面i+1是虚部，这样存储，所以数组大小为2*N，不过我们这里虚部全置0了???待补充；

float fft_inputbuf[FFT_LENGTH*2];    //FFT输入数组

 参数3：用于设置正变换和逆变换，ifftFlag=0表示正变换，ifftFlag=1表示逆变换。

参数4：用于设置输出位反转，bitReverseFlag=1表示使能，bitReverseFlag=0表示禁止。

3，测试

for(i=0;i<FFT_LENGTH;i++)//生成信号序列
		{
			 fft_inputbuf[2*i]=1+
							   1*arm_sin_f32(2*PI*i/FFT_LENGTH)+
							   2*arm_sin_f32(2*PI*i*4/FFT_LENGTH)+
							   4*arm_cos_f32(2*PI*i*8/FFT_LENGTH);	//生成输入信号实部
			 fft_inputbuf[2*i+1]=0;//虚部全部�????0
		}


	  // data = arm_sin_f32(3.1415926/6);		//对sin(PI/6 = 30�???????????)正弦值，求浮点�?�，理论上应为：1/2�???????????0.5
	  // printf("sin=%.2f\r\n",data);

	  	__HAL_TIM_SET_COUNTER(&htim3,0);//重设TIM3定时器的计数器�??
		timeout=0;
		arm_cfft_f32(&arm_cfft_sR_f32_len1024,fft_inputbuf,ifftFlag,doBitReverse);

		//arm_cfft_radix2_f32(&scfft,fft_inputbuf);	//FFT计算（基4�????
		arm_cmplx_mag_f32(fft_inputbuf,fft_outputbuf,FFT_LENGTH);   //把运算结果复数求模得幅�??
		//temp = ADC1247_Read();
		time=__HAL_TIM_GET_COUNTER(&htim3)+(uint32_t)timeout*50000;//计算�????????用时�????????
		printf("time = %0.3fms\r\n",((float)time*10)/1000);

		for(i=0;i<FFT_LENGTH;i++)
		{
			//printf("fft_outputbuf[%d]:%f\r\n",i,fft_outputbuf[i]);
			printf("%f ",i,fft_outputbuf[i]);
		}

 

总结：

1，采样率Fs ，采样点N ，则采样分辨力 = Fs/N；也就是，FFT之后，根据采样点个数等分Fs，某点n所表示的频率为：Fn=(n-1)*Fs/N。如果要提高频率分辨力，则必须增加采样点数。

2，FFT函数输入数据，是一个2*N大小的数组。

3，FFT函数输出数据。

假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。而第一个点就是直流分量，它的模值就是直流分量的N倍

        假设FFT之后某点n用复数a+bi表示，那么这个复数的模就是An=根号a*a+b*b，相位就是Pn=atan2(b,a)。根据以上的结果，就可以计算出n点（n≠1，且n<=N/2）对应的信号的表达式为：An/(N/2)*cos(2*pi*Fn*t+Pn)，即2*An/N*cos(2*pi*Fn*t+Pn)。对于n=1点的信号，是直流分量，幅度即为A1/N。

参考文章

【STM32H7的DSP教程】第30章 STM32H7复数浮点FFT（支持单精度和双精度）_嵌入式系统OS的博客-CSDN博客_arm_cfft_f32(&arm_cfft_sr_f32_len4096, fft_input_f

【转】FFT的matlab实现与结果解释_落yi翊的博客-CSDN博客

FFT结果的物理意义_修补桑的博客-CSDN博客_已知信号采样率fs=2000hz,信号有两个频率分量:f1=300hz,a1=1; f2=304hz