238. 除自身以外数组的乘积（中等）

方法一：左右乘积列表

思路

• 除了 nums[i] 以外各元素的积，就等同于 nums[i] 左边元素的乘积 * 右边元素的乘积，因此，我们可以计算出两个乘积列表 ，最后再经过一次遍历，将对应位置上的结果相乘，得到最终答案。

  

代码

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> ans(n, 1), left(n, 1), right(n, 1);
        for(int i=1; i<n; ++i){
            left[i] = left[i-1] * nums[i-1];
        }
        for(int i=n-2; i>=0; --i){
            right[i] = right[i+1] * nums[i+1];
        }
        for(int i=0; i<n; ++i){
            ans[i] = left[i] * right[i];
        }
        return ans;
    }
};

方法二：空间优化

思路

• 题目进一步要求：空间复杂度为 O（1） ，因此我们不可以使用 left 和 right 数组；
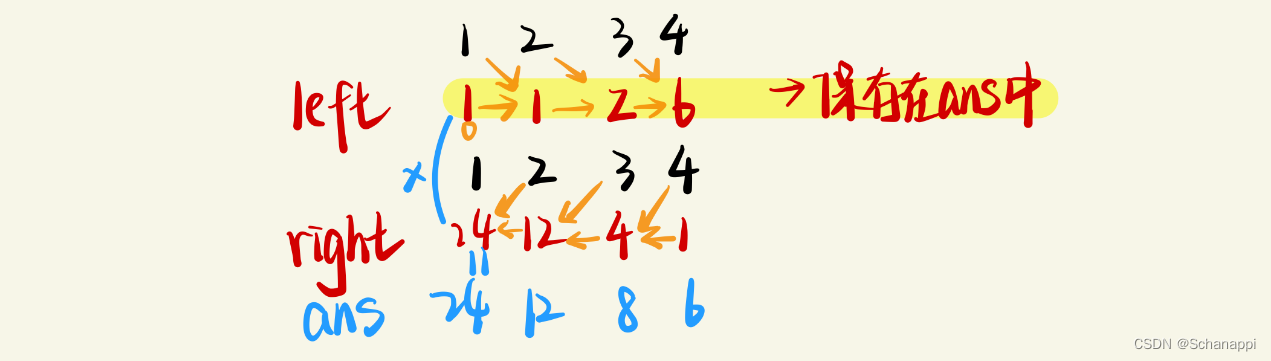
• 通过观察不难发现，从 i = 2 开始， left[i] 只和 left[i-1] 、nums[i-1] 有关，因此我们可以进行空间压缩， 用变量来替代数组，left 的状态更新：left = left * nums[i]; ，此时只需要把当前的left 存入 ans[i] 即可；
• 同样地，对于 right[i] 而言，它只和 right[i+1] 、nums[i+1] 有关，所以 right 的状态更新为：right = right * nums[i]; ，此时只需要将当前的 right 和 已有的 ans[i] 相乘，得到最终结果。
• 初始化：int left = nums[0] , right = nums[n-1];
  

代码

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> ans(n, 1);
        int left = nums[0] , right = nums[n-1];
        for(int i=1; i<n; ++i){
            ans[i] = left;
            left = left * nums[i];
        }
        for(int i=n-2; i>=0; --i){
            ans[i] *= right;
            right = right * nums[i];
        }
        return ans;
    }
};