2023-05-24每日一题
一、题目编号
1377. T 秒后青蛙的位置
二、题目链接
点击跳转到题目位置
三、题目描述
给你一棵由 n 个顶点组成的无向树,顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下:
- 在一秒内,青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点(如果它们直接相连)。
- 青蛙无法跳回已经访问过的顶点。
- 如果青蛙可以跳到多个不同顶点,那么它跳到其中任意一个顶点上的机率都相同。
- 无向树的边用数组 edges 描述,其中 edges[i] = [ai, bi] 意味着存在一条直接连通 ai 和 bi 两个顶点的边。
返回青蛙在 t 秒后位于目标顶点 target 上的概率。与实际答案相差不超过 10-5 的结果将被视为正确答案。
四、解题代码
class Solution {
double dfs(vector<vector<int>> &Edge, int *hash, int node, int time, int t, int target){
if(t == time){
if(node == target){
return 1;
}
return 0;
}
double cnt = 0;
double probability = 0;
for(int i = 0; i < Edge[node].size(); ++i){
int next_node = Edge[node][i];
if(hash[next_node] == 0){
cnt++;
hash[next_node] = 1;
probability += dfs(Edge, hash, next_node, time+1, t, target);
hash[next_node] = 0;
}
}
if(cnt == 0){
return dfs(Edge, hash, node, t, t, target);
}
return probability / cnt;
}
public:
double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
vector<vector<int>> Edge;
Edge.resize(110);
int m = edges.size();
for(int i = 0; i < m; ++i){
int x = edges[i][0];
int y = edges[i][1];
Edge[x].push_back(y);
Edge[y].push_back(x);
}
int hash[110];
memset(hash, 0, sizeof(hash));
hash[1] = 1;
return dfs(Edge, hash, 1, 0, t, target);
}
};
五、解题思路
(1) 这道题目是一道与概率论相关的题目,所以我们得先理清楚如何算出概率,才能写出代码。
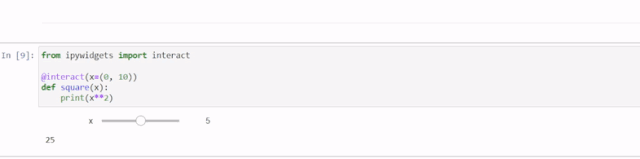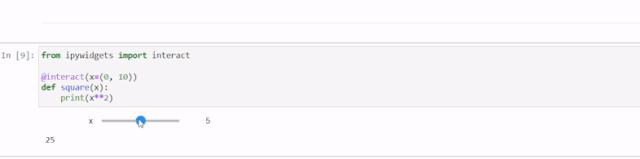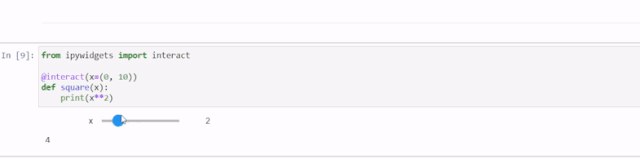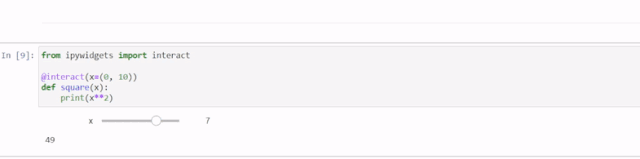
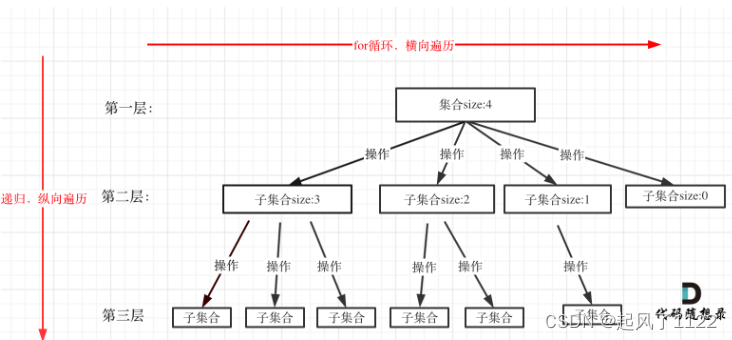
这是题目给出的一个例子,t = 2, target = 4。那么我们最终的概率是多少呢,是1 / 3 * 1 / 2。那么我们知晓了概率计算方式,便可以思考下面一个问题了。
(2) 对于结点4,已经打成目标了,所以可以返回1。对于结点6,因为达不成目标了,所以返回0。那么对于结点2,后继结点是2个,可能的概率为1 / 2。 那么同理,对于结点1,后继结点是3,那么概率为(1 / 2)/ 3.
(3) 按照上述的思路思考完毕,这道题目可以用深度优先搜索的方式来求概率,如果最终时间到了或者没有后继结点,如果达到目标节点,则返回1,否则返回0。每一点的概率等于到达的可能性除以后继结点即可。
(4) 用邻接表来辅助进行深度优先搜索。