题目

给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。

示例

输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出： True
说明：有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。

题解

该题目的意思是给你一堆数据nums，你要把这些数据划分成k个集合，每个集合里的数据和是相同的。以nums=[1,3, 3, 2, 3, 5, 2, 1],k=4为例来说明一下该题目的思路。
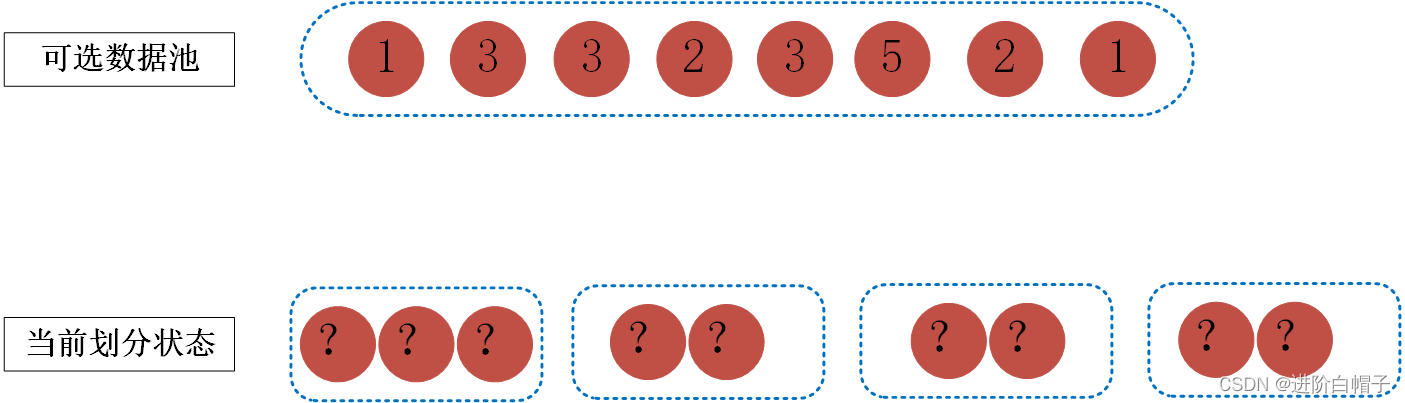
在这里插入图片描述
首先来分析题目，题目的意思就是把给定的可选数据池分到k=4个桶里，每个桶中的数据和相同，那很显示有一个特性就是k*每个桶中数据和=可选数据池所有数据的和，在这个示例里每个桶中包含的数据和为5。通过这一步分析我们能得到一个新的条件即每个桶中数据和，同时也能确定两个边界：1 必须满足sum(nums)%k=0，即所有数据和必须能被k整除；2 len(num)>k,即可选数据池的数据个数必须大于k不然的话k个桶中就会出现空集。

下面探索一下该题目的可行算法。初始状态可选数据集为当前数据列表，所有的桶中均为空。
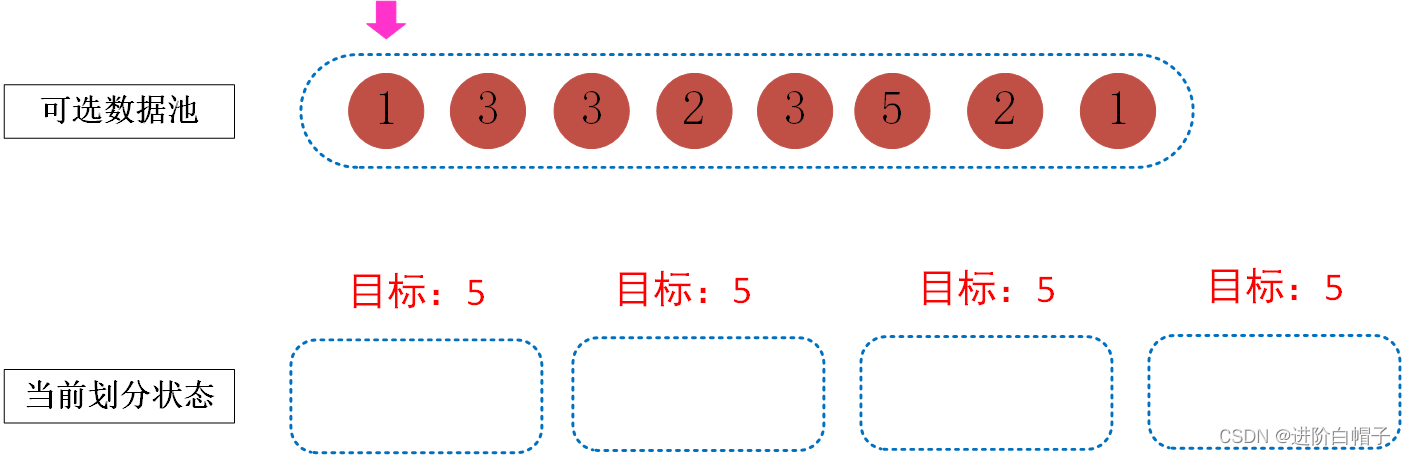
在这里插入图片描述
由于目标是为了让每个桶中的数据达到5。我们可以遍历可选择数据池，选择数据放到桶中。由于当前桶中均为空是一样的，可以随意选择一个桶放入数据1，结果如下图所示。

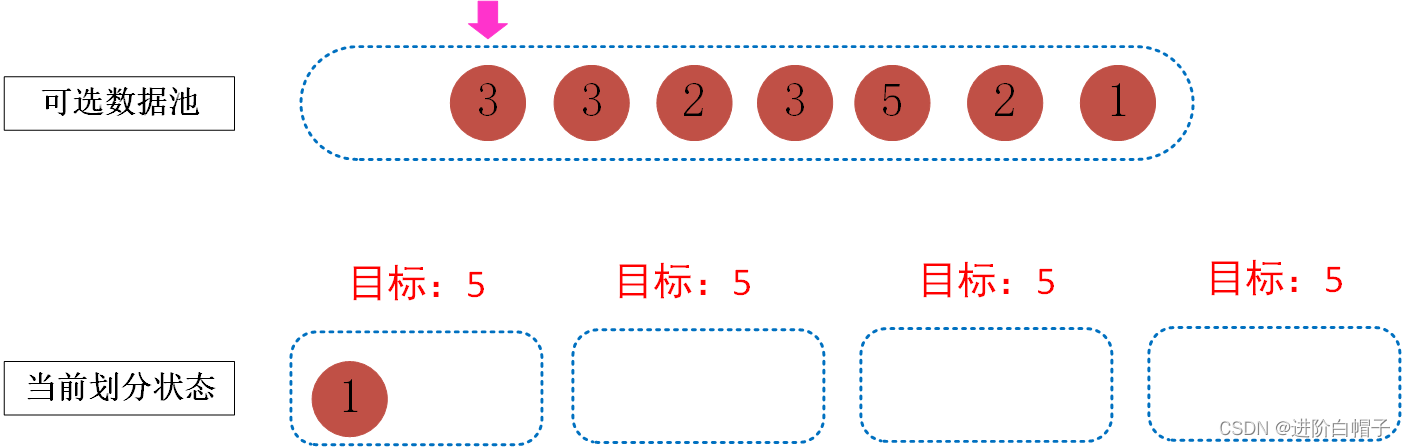
接下来处理数字3，在这里当前的桶中有一个里面有数据了，这里我们首先需要尽可以找到一组数来填满一个桶，然后再填下一个桶。把3放到第一个桶中，这样第一个桶中的数据和就变成了4。
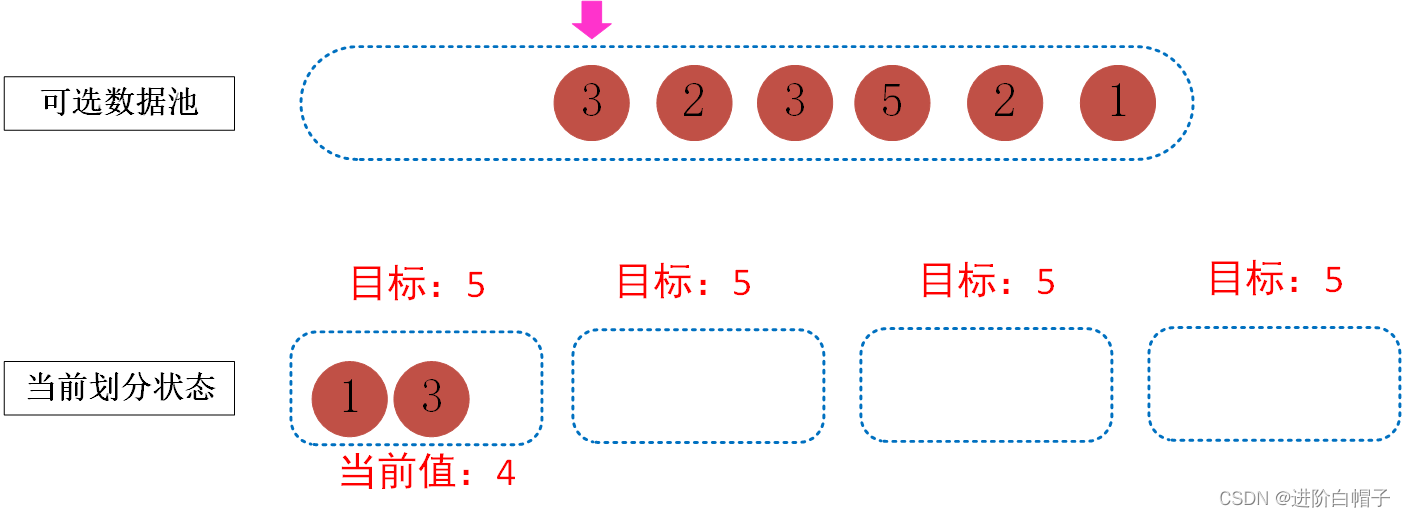
在这里插入图片描述
继续下去，碰到当前数据池中第2个3，由于该数据如果放到第一个桶中的话会超出目标，因此，跳过3，直到1才能满足要求。最终结果如下图。

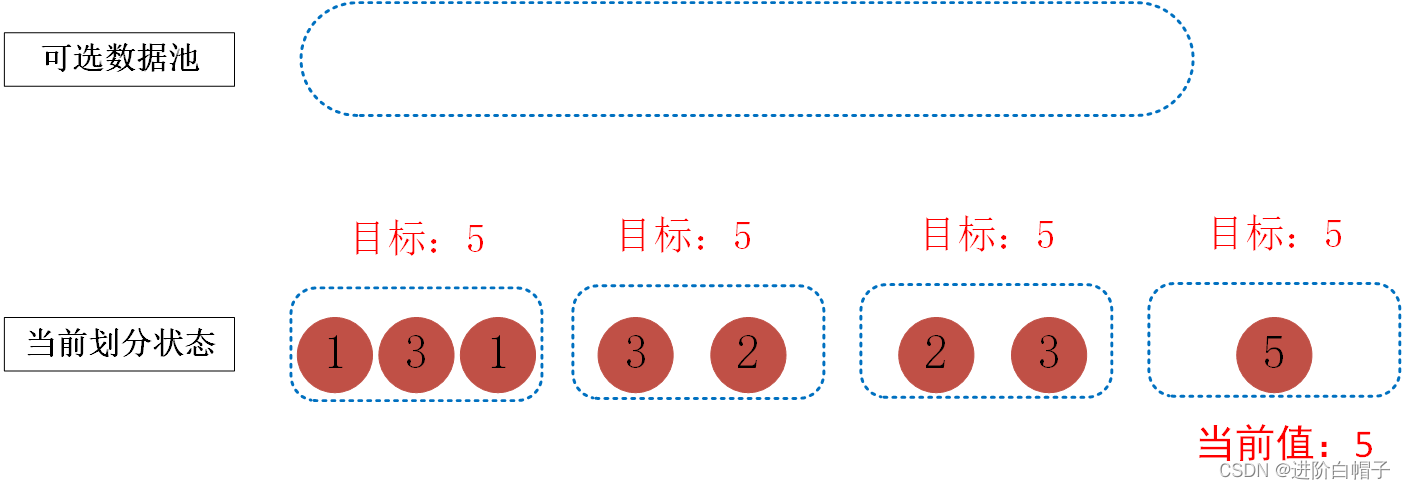
针对该问题大体思路已出现，但是还有一个关键的问题即第一个桶中选完1之后，3一定是放在第一个桶中的么，其实不一定。这里是本题的关键，其中涉及到递归或回溯思想来解决该问题。

其实我们在之前的步骤中也看到了，我们进行划分的时候只跟两个变量有关，一是当前值，一是可选数据池，我们每一步的目标均是希望实现剩下的所有桶均达到目标值。如果一个桶满了当前值就需要再从0开始算，如下图所示。

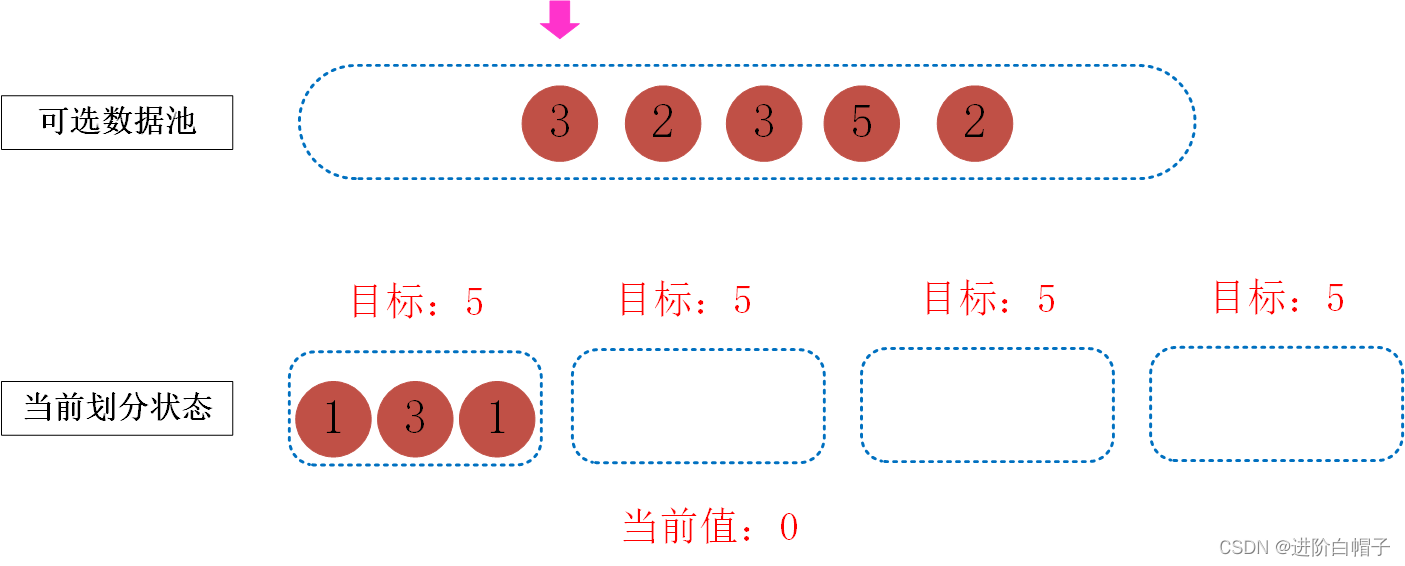
在这里插入图片描述
我们的递归函数的已经很明显了：

输入：可选数据池，当前值
输出：是否能填充剩下的桶
递归过程：终止条件是可选数据池数据为空，如果已选数据与当前值大于目标则跳过，否则更新当前值与可选择数据池执行递归过程。

到些基础版本的递归代码就可以手写了。

class Solution:
    def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:
        all_sum=sum(nums)
        sub_sum,rest=divmod(all_sum,k)
        #边界，判断是不是
        if rest:
            return False
        if len(nums)<k:
            return False
        def dfs(choosable_list,curr_value):
            #如果可选数据池为空则分配完成
            if not choosable_list:
                return True
            for idx in range(len(choosable_list)):
                #如果当前数与靠近的数据之处大于sub_sum则跳过
                if choosable_list[idx]+curr_value>sub_sum:
                    break
                #复制choosable_list
                choosable_list_copy=[item for item in choosable_list]
                del choosable_list_copy[idx]
                if dfs(choosable_list_copy,(curr_value+choosable_list[idx])%sub_sum):
                    return True
            return False
        return dfs(nums,0)

代码会超时。这里需要进步一优化。

状态压缩

首先考虑的是状态压缩，因为chooselist使用的话需要复杂副本，占用较大空间。这里可选数据池满足状态压缩的条件，要求的长度小于16，使用32位二进制可以有效表示可选数据的状态。这里二进制中的1表示nums列表中该位置的数据可选，0表示该位置不可选择。初始状态是(1<<n)-1，n是nums的长度，表示0到n-1位全为1。这里与上面使用列表不同，需要判断当前状态是否可选择，state>>i&1即判断nums[i]的数据是否可选。在递归时，需要更新可选择列表的状态，state^ (1<<i)是利用位运算把第i位的状态变成0，这里^ 有个性质，0与任何数做^ 运算均不变，而当前i位置是1再与一个i位置为1做^运算即变为0。这样基于状态压缩的代码即如下实现。

class Solution:
    def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:
        n=len(nums)
        all_sum=sum(nums)
        sub_sum,rest=divmod(all_sum,k)
        #边界
        if rest:
            return False
        #如果nums的长度小于k
        if n<k:
            return False
        def dfs(state,curr_value):
            #如果没有可选择的数据则分配完成
            if state==0:
                return True
            for i in range(n):
                #判断i位置数据是否可选
                if state>>i&1:
                    #判断该数据是否可以与curr_value分到一起
                    if nums[i]+curr_value>sub_sum:
                        break
                    if dfs(state^(1<<i),(curr_value+nums[i])%sub_sum):
                        return True
            return False
        return dfs((1<<n)-1,0)

依然超时。

记忆化搜索

上面代码超时的原因是递归过程会有大量的重复计算，这里显示考虑记忆化搜索，python中记忆化搜索实现非常简单，在递归函数前加上@cache装饰器。

class Solution:
    def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:
        n=len(nums)
        all_sum=sum(nums)
        sub_sum,rest=divmod(all_sum,k)
        #边界
        if rest:
            return False
        #如果nums的长度小于k
        if n<k:
            return False
        @cache
        def dfs(state,curr_value):
            #如果没有可选择的数据则分配完成
            if state==0:
                return True
            for i in range(n):
                #判断i位置数据是否可选
                if state>>i&1:
                    #判断该数据是否可以与curr_value分到一起
                    if nums[i]+curr_value>sub_sum:
                        break
                    if dfs(state^(1<<i),(curr_value+nums[i])%sub_sum):
                        return True
            return False
        return dfs((1<<n)-1,0)