代码随想录刷题记录day34 动态规划理论基础+斐波那契数+爬楼梯+使用最小花费爬楼梯

动态规划理论基础

解决的问题

由前一个状态决定了后一个的状态，可以用动态规划来解决。贪心是没有状态推导的。

解题步骤

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

打印dp数组来验证

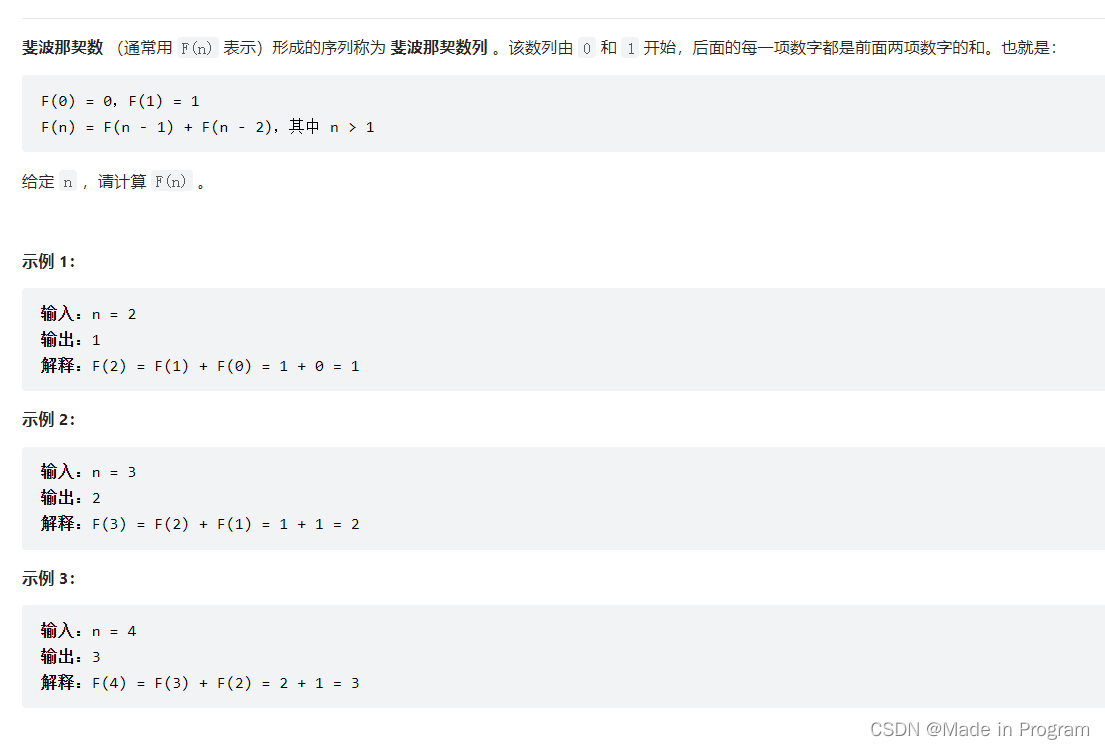
509. 斐波那契数

思想

当前的状态是由之前的状态推导出来的，所以可以用动态规划来解决此类问题。

动态规划五步曲

1. 确定dp数组（dp table）以及下标的含义

   dp[i]表示第i个斐波那契数

2. 确定递推公式

   题目给了递推公式了dp[i]=dp[i-1]+dp[i-2]

3. dp数组如何初始化

   题目已经给了初始数值 dp[0]=0,dp[1]=1

4. 确定遍历顺序

   当前状态是依赖之前的状态的，所以是从前往后遍历的

5. 举例推导dp数组

   0 1 1 2 3 5 8 13 21 34 55

代码

class Solution {
    // public int fib(int n) {
    //     int f0=0,f1=1;
    //     if(n==0) return 0;
    //     if(n==1) return 1;
    //     int sum=0;
    //     for(int i=2;i<=n;i++){
    //         sum=f1+f0;
    //         f0=f1;
    //         f1=sum;
    //     }

    //     return sum;
    // }

    public int fib(int n){
        //动态规划五步曲
        //1/确定dp数组（dp table）以及下标的含义  dp[i]表示 第i个斐波那契数
        //2.确定递推公式 dp[i]=dp[i-1]+dp[i-2]
        //3.dp数组如何初始化 dp[0]=0;dp[1]=1
        //4.确定遍历顺序 前面的状态推出后面的状态 所以是从前往后遍历
        //5.举例推导dp数组  dp[2]=dp[1]+dp[0];

        int [] dp=new int[n+1];
        if(n==0) return 0;
        if(n==1) return 1;
        dp[0]=0;
        dp[1]=1;
        for(int i=2;i<=n;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }

        return dp[n];

    }
}

70. 爬楼梯

思想

动态规划五步曲

1. 确定dp数组（dp table）以及下标的含义

   dp[i]表示到达第i个台阶的方法

2. 确定递推公式

   dp[i-1]表示到达第i-1个台阶的方法

   dp[i-2]表示到达第i-2个台阶的方法

   dp[i]只能从i-1个台阶和i-2个台阶跳过来，所以dp[i]=dp[i-1]+dp[i-2];

3. dp数组如何初始化

   n从1开始

   dp[1]=1;

   dp[2]=2;

4. 确定遍历顺序

   当前状态是依赖之前的状态的，所以是从前往后遍历的

5. 举例推导dp数组

   1 2 3 5 8

代码

class Solution {
    public int climbStairs(int n) {
        //动态规划 五步曲
        //1.确定 dp[i] 和下标
        //2.动态规划方程
        //3.初始化
        //4..遍历顺序
        //5.举例推导

        //dp[i] 表示跳到第i个台阶的方法数
        //dp[i]=dp[i-1]+dp[i-2];
        //dp[1]跳到第一个台阶，有一种  跳到第二个台阶有2种
        if(n==1) return 1;
        int [] dp=new int[n+1];
        dp[1]=1;
        dp[2]=2;
        //当前台阶需要之前台阶的状态
        for(int i=3;i<=n;i++){
            dp[i]=dp[i-1]+dp[i-2];
            //System.out.println(dp[i]);
        }

        return dp[n];
    }
}

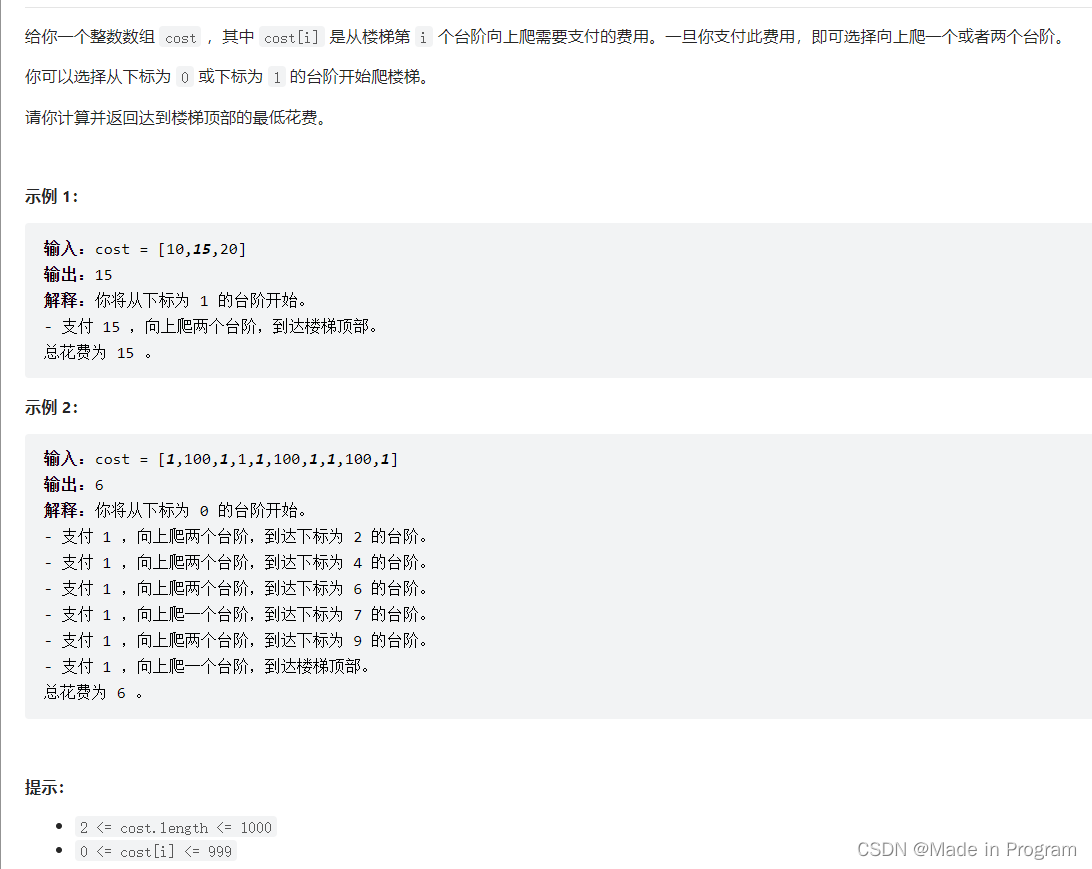
746. 使用最小花费爬楼梯

思想

动态规划五步曲

1. 确定dp数组（dp table）以及下标的含义

   dp[i]表示到达第i个台阶所需的最小的花费

2. 确定递推公式

   dp[i-1]表示到达第i-1个台阶所需的最小的花费

   dp[i-2]表示到达第i-2个台阶所需的最小的花费

   dp[i]只能从i-1个台阶和i-2个台阶跳过来，所以dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);

3. dp数组如何初始化

   从第0个台阶或者第1个台阶开始跳，dp[0]=0,dp[1]=0;

4. 确定遍历顺序

   当前状态是依赖之前的状态的，所以是从前往后遍历的

5. 举例推导dp数组

   cost=[1,100,1,1,1,100,1,1,100,1]

   dp[i]=[0,0,1,2,2,3,3,4,4,5,6]

代码

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        //递归五部曲
        //1.确定dp数组含义 及下标的含义
        //2.确定递推公式
        //3.初始化
        //4.遍历顺序
        //5.模拟过程

        //cost[i] 从楼梯第i个台阶向上爬需要支付的费用
        //dp[i] 爬到第i个台阶 所需要的最小的费用
        //dp[i-1]爬到第i-1个台阶 所需要的最小的费用
        //dp[i-2]爬到第i-2个台阶 所需要的最小的费用
        //dp[2]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);


        int[] dp=new int[cost.length+1];
        dp[0]=0;
        dp[1]=0;

        for(int i=2;i<=cost.length;i++){
            dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
            //System.out.println(dp[i]);
        }

        return dp[cost.length];

    }
}