文章目录
- 第1讲:概论
- 一、课程内容
- 课程简介
- 课程教材
- 慕课堂
- 二、课程组成结构
- 计算机系统组成
- 计算机软硬件概念
- 以运算器为中心
- 现代计算机的存储器为中心
- 硬件各部分关系
- 内存基本组成
- 运算器基本组成
- 累加器(相当于寄存器)
- 控制器组成
- 第2讲:计算机系统层次结构
- 三、计算机系统层次结构
- 计算器语言比较
- 四、计算机的工作过程
- (1)取数指令(从存储器中取数据)
- (2)存数指令(向存储器中写数据)
- 五、机器字长
- 六、存储容量
- 七、运算速度
- 速度衡量方法
- 八、程序执行的时间度量方法
- 信息表示
- 数据表示
- 无符号数
- 有符号数
- 位串(比符号数更为广泛)
- 带权的位置数制
- 十进制
- 二进制
- 十六进制
- 进制相互转化表
- 十进制转二进制
- 十进制转十六进制
- 总结:十进制转二四八十六进制
- 总结:二四八十六进制转十进制
- BCD码表示法(自学)
- BCD码的分类和运算
- BCD码的用途
- BCD码分类
- 有权BCD码
- 无权BCD码
- 8421BCD码运算
- 例题1:
- 余三码及运算
- 例2:
- 第3讲:定点数的数据表示
- 无符号数和有符号数
- 无符号数
- 有符号数
- 有符号机器数的编码形式
- 定点机器数和真值
- 原码表示法
- 1.原码的定义
- 整数原码
- 小数原码
- 例一:已知原码求真值
- 例二:已知真值求原码
- 2.原码表示法总结
- 定点数的补码表示法
- 一、补码表示法
- 结论:
- 二、补码定义
- 整数
- 小数
- 三、求补码表示的方法
- 例一:已知小数补码求真值
- 例二:已知整数补码求真值
- 例三:已知负数补码求真值
- 证明:已知[y]补,求[-y]补
- 求补的应用:把所有减法变加法
- 例四:几个特殊值的机器值
- 四、反码的表示法
- 整数
- 小数
- 例一:已知整数反码求真值
- 例二:求0的反码
- 总结:三种机器数
- 各种机器数的数值表示(机器字长8位)
- 定点数加减法
- 一、补码加减运算公式
- 例题1:加法
- 例题2:减法
- 第4讲:定点数加减法器实现
- 一、1-bit加法器
- 二、n-bit加法器
- n-bit减法器
- 三、加减法器
- 定点数加减法的溢出判断
- 一、溢出问题(练习1)
- 练习2
- 2038年问题
- 二、溢出概念
- 三、溢出判断
- 1.一位符号位判断溢出
- 2.符号位进位CF和最高有效位C进位判断溢出
- 3.双符号位判断溢出
- 总结:补码加减法硬件电路
- 定点数移位运算
- 一、移位运算意思
- 二、算术移位和逻辑移位
- 三、算术移位(有符号数移位)规则
- 例1
- 例2
- 四、移位运算硬件实现
- 第5讲 计算方法-定点数算术逻辑单元
- 一、串行进位加法器的延迟问题
- 二、分析n-bit串行加法器的进位
- image-20221109165849153
- 三、4-bit先行进位电路
- 四、4-bit超前进位加法器
- 五、16-bit快速加法器
- 六、16-bit更快速加法器
- 算术逻辑单元
- 一、算术逻辑单元概念
- 二、设计一个特定功能的算术逻辑单元
- 三、一款商用算术逻辑单元芯片74181
- 四、多位ALU
- 第9讲 存储器存储结构
- 半导体存储器概述
- 一、按存储器分类
- EPROM
- Flash存储器
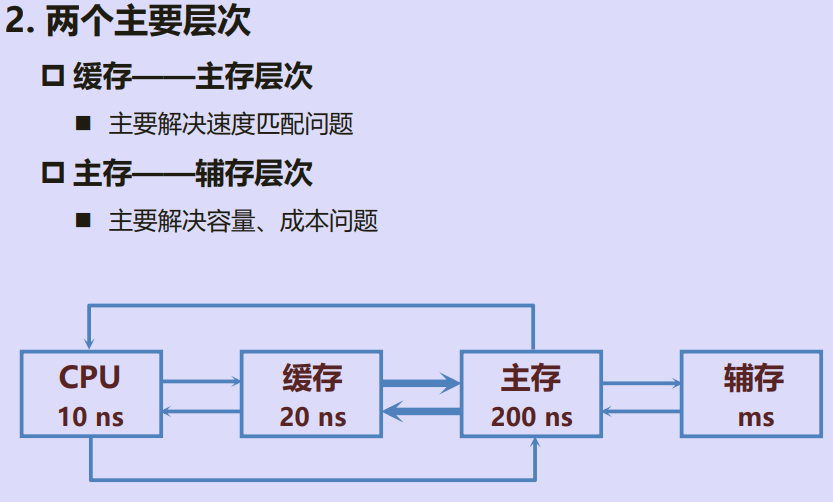
- 二、存储器的层次结构
- 1. 存储器各层位置及特点
- 三、主存和cpu的联系
- 读操作
- 写操作
- 四、半导体存储芯片的基本结构
- 静态随机存储器的存储元
- 静态随机存储器基本单元电路(存储元)
- 静态存储元的读操作
- 静态存储元的写操作
- 静态储存元的抽象表示
- 动态随机存储器的存储元
- 动态随机存储器基本单元电路
- 存储元读过程
- 存储元写过程
- 动态存储元简化
- 单管动态存储元
- 动态存储元的抽象
- 随机存储器的存储字结构
- 四、半导体存储芯片的基本结构
- 译码器&编码器
- 译码器(解码器)
- 半导体储存芯片的译码驱动
- (1)线选法
- (2)重合法
- 优点
- 单管动态存储元
- 动态存储元的抽象
- 随机存储器的存储字结构
- 四、半导体存储芯片的基本结构
- 译码器&编码器
- 译码器(解码器)
- 半导体储存芯片的译码驱动
- (1)线选法
- (2)重合法
- 优点
第1讲:概论
一、课程内容
课程简介

课程教材


慕课堂

二、课程组成结构
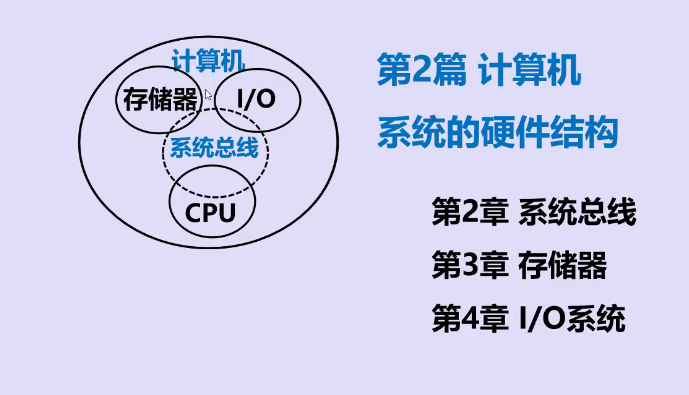
计算机系统组成
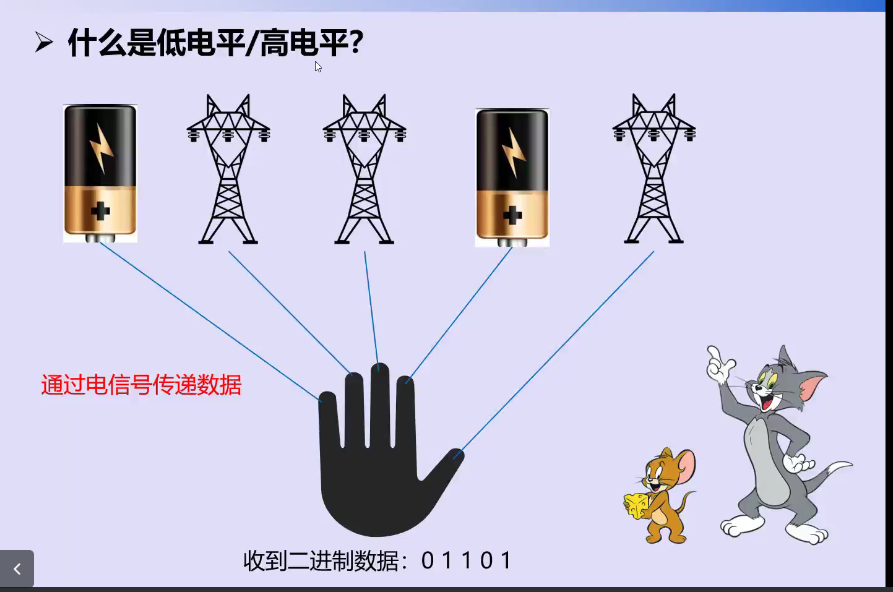

计算机软硬件概念
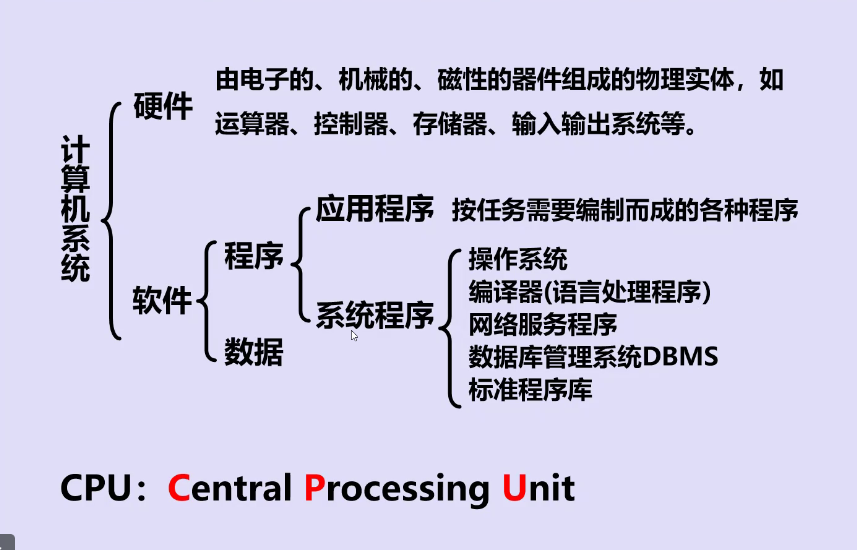
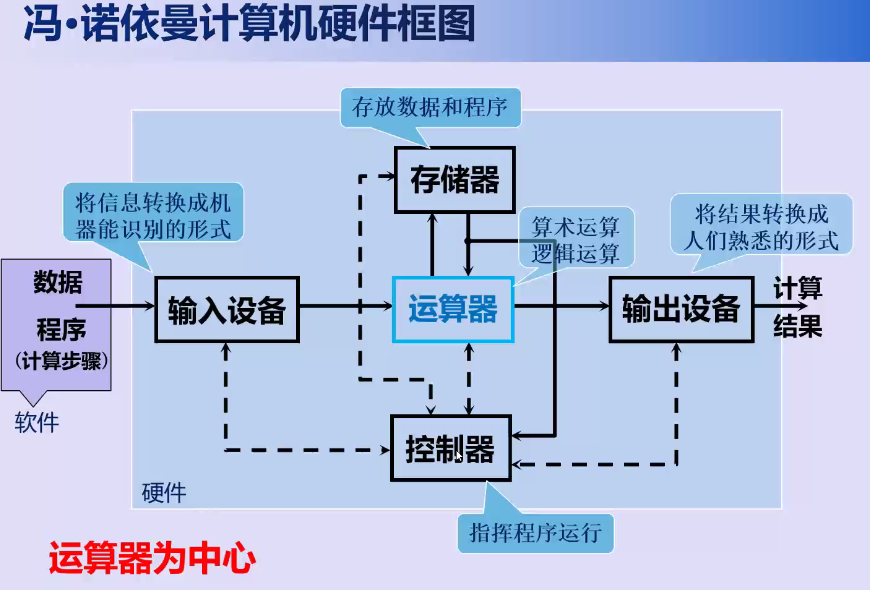

以运算器为中心
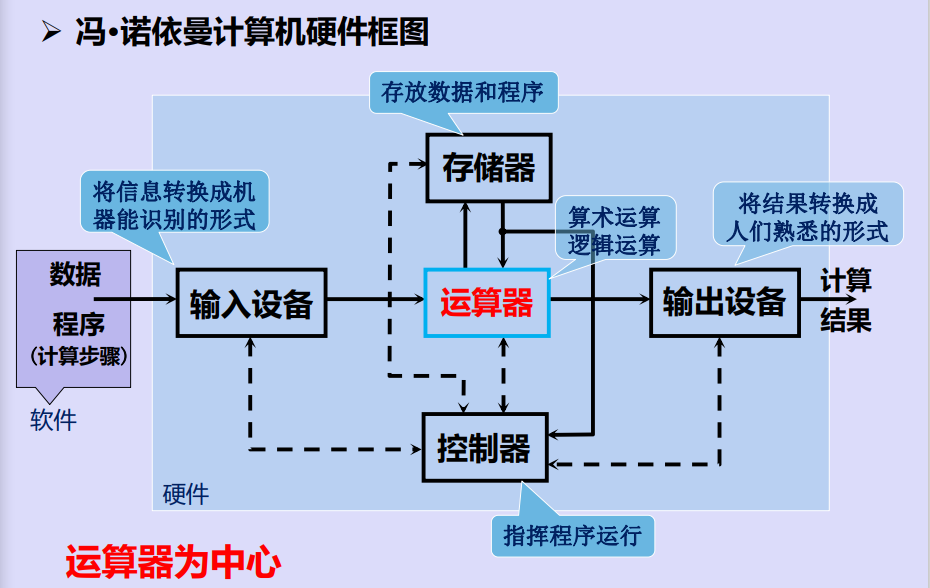
现代计算机的存储器为中心
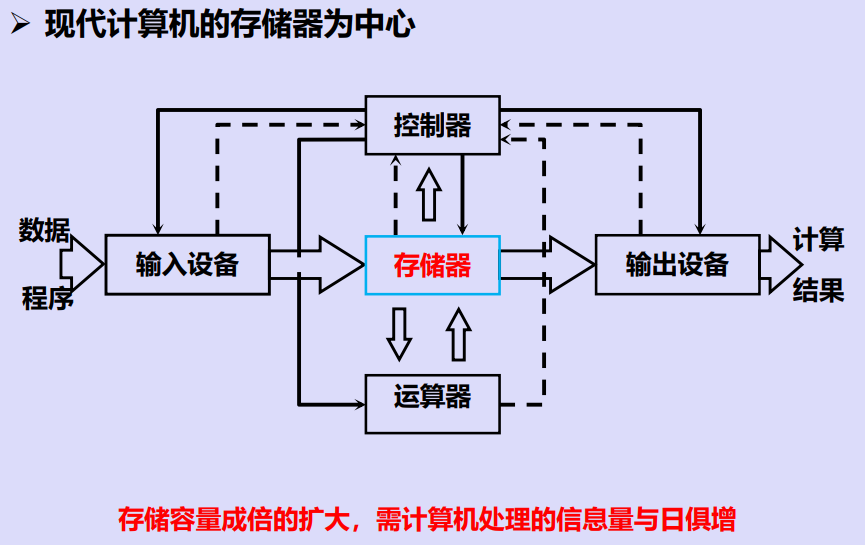
硬件各部分关系
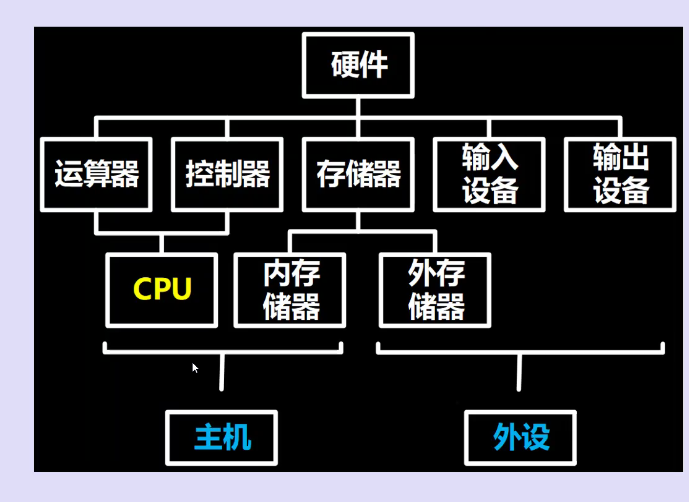
内存基本组成


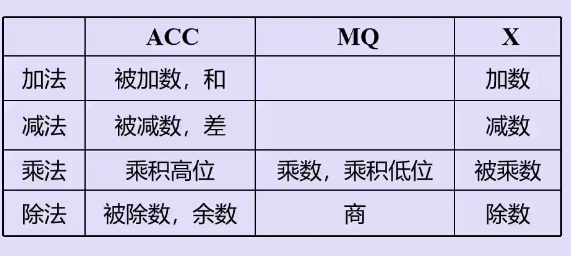
运算器基本组成

累加器(相当于寄存器)
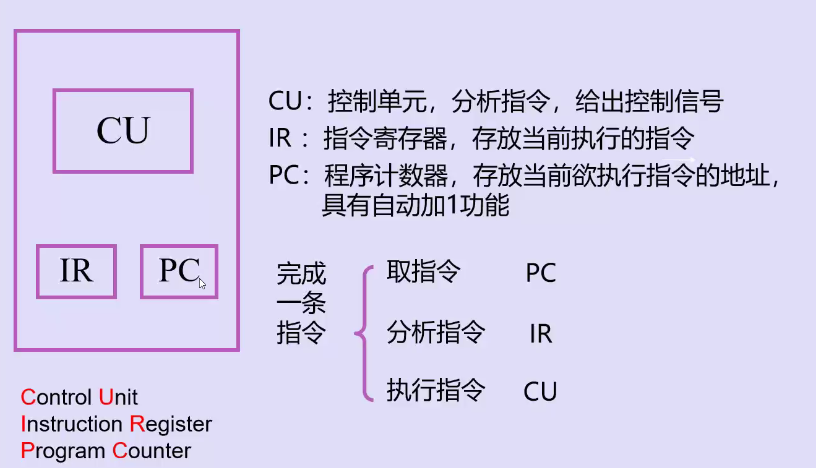
控制器组成
第2讲:计算机系统层次结构
三、计算机系统层次结构
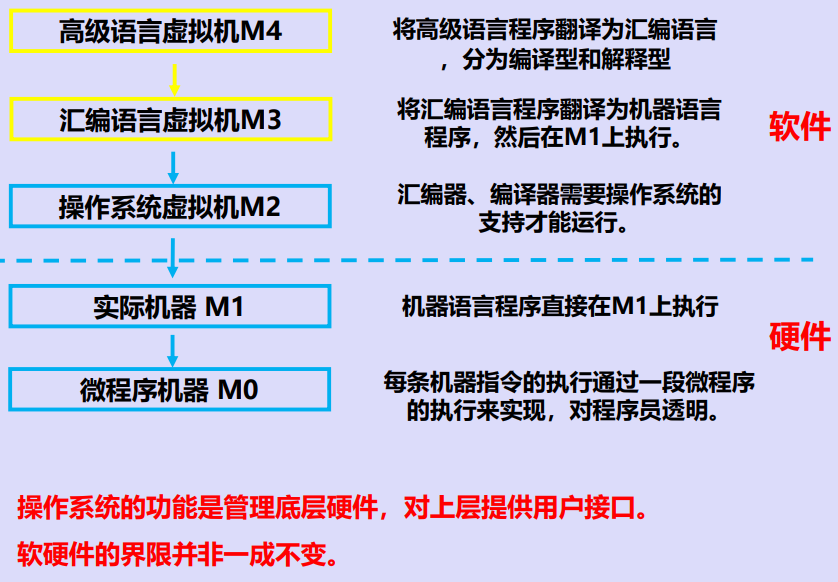
计算器语言比较
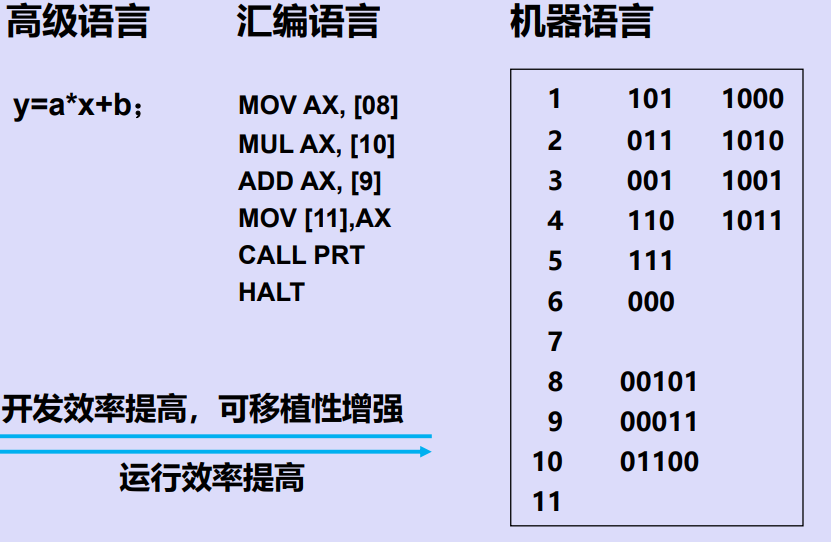
四、计算机的工作过程
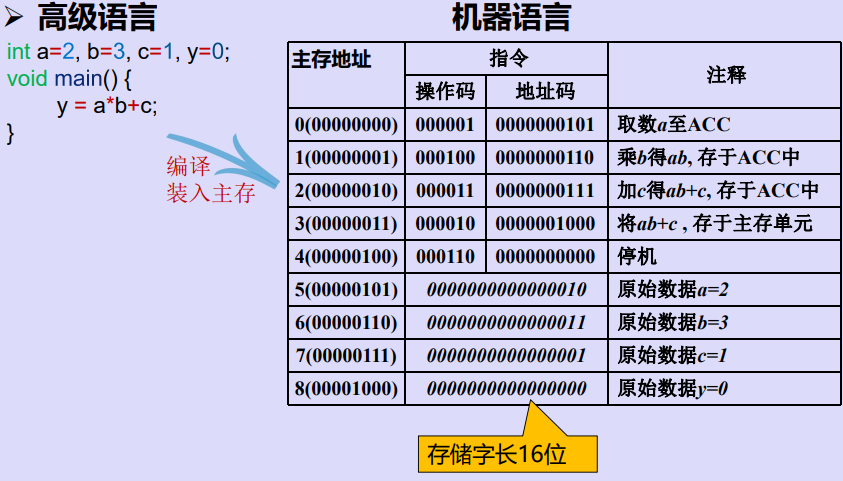
完整指令执行流程——读取指令、分析指令、执行指令
(1)取数指令(从存储器中取数据)
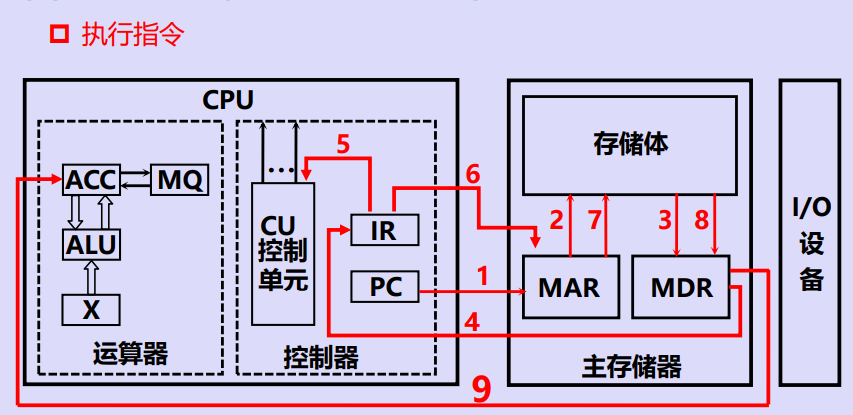
(2)存数指令(向存储器中写数据)
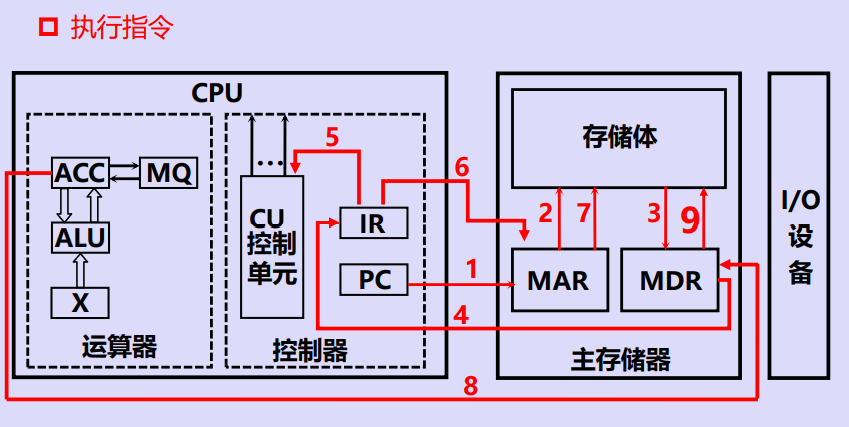
五、机器字长
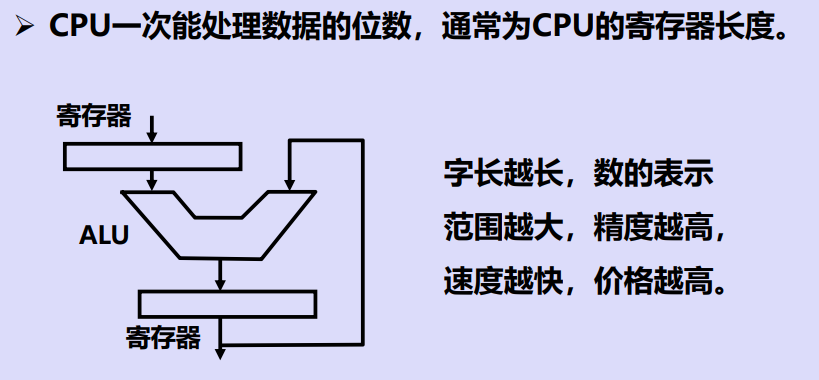
六、存储容量

七、运算速度
速度衡量方法

八、程序执行的时间度量方法

信息表示

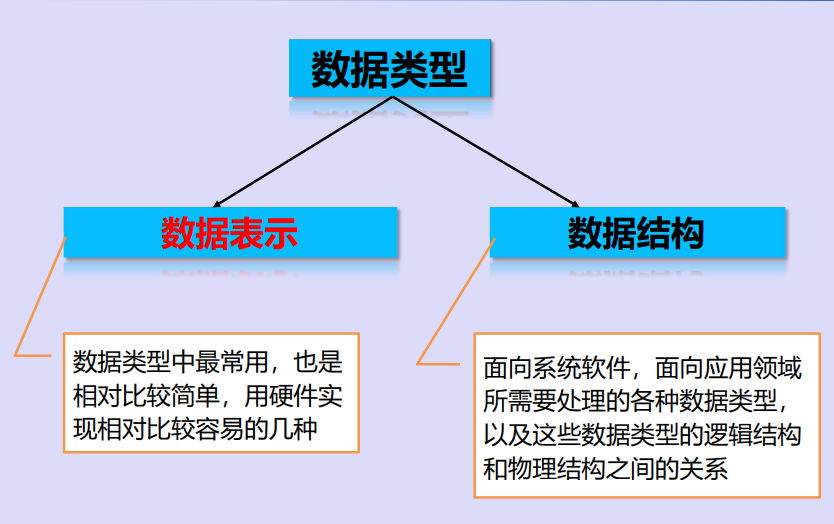

数据表示

无符号数

有符号数

位串(比符号数更为广泛)

带权的位置数制

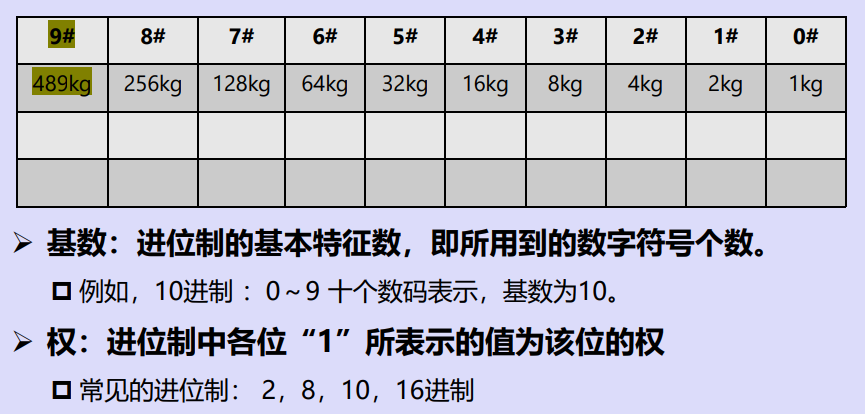
十进制

二进制

十六进制

进制相互转化表
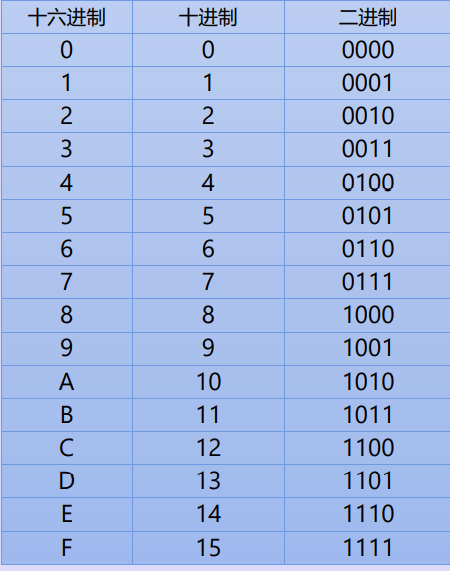
十进制转二进制
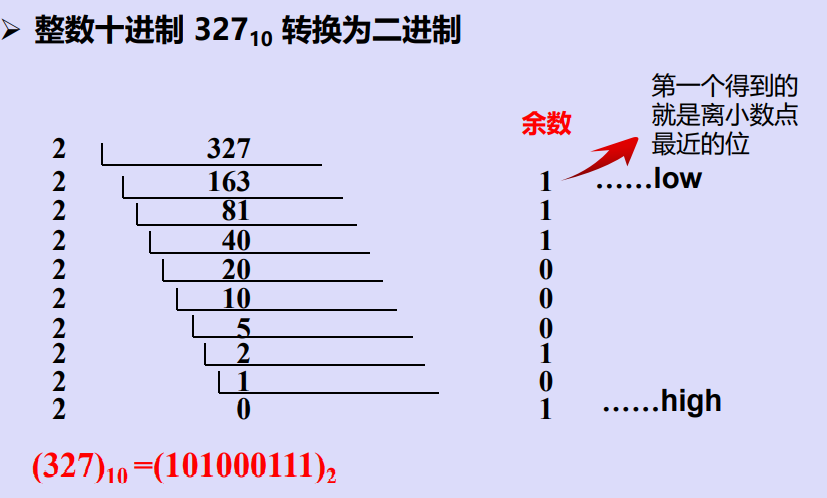


十进制转十六进制

总结:十进制转二四八十六进制

总结:二四八十六进制转十进制

BCD码表示法(自学)
BCD码的分类和运算

BCD码的用途

BCD码分类

有权BCD码
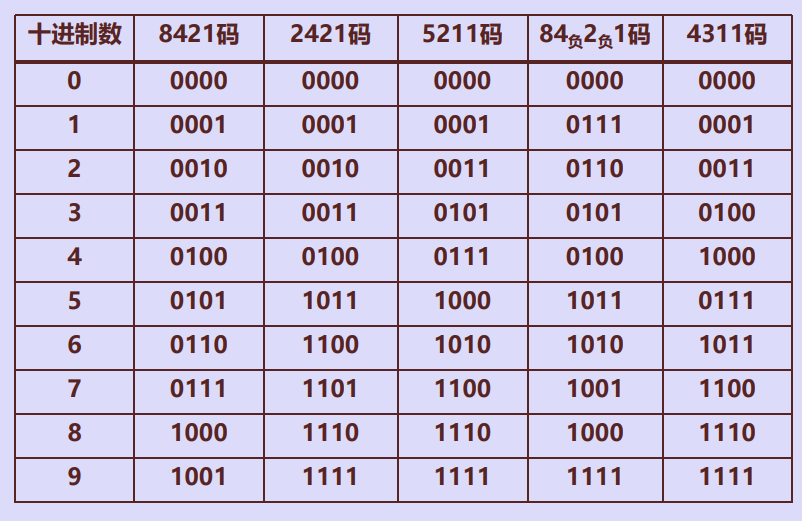
无权BCD码
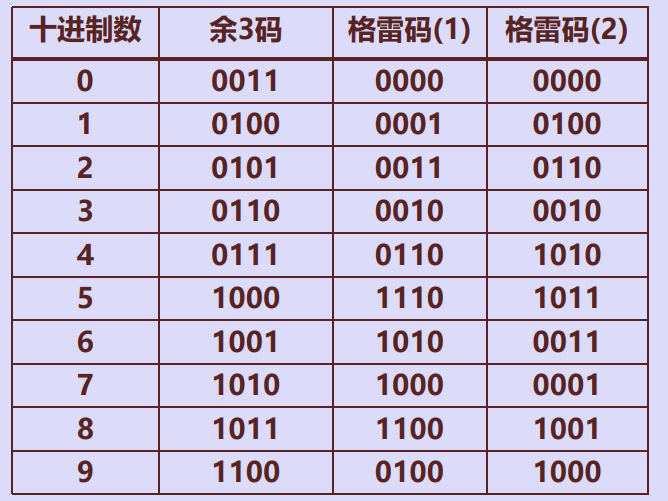
8421BCD码运算

例题1:

余三码及运算

例2:

第3讲:定点数的数据表示
无符号数和有符号数

无符号数
没有符号的数,寄存器的每一位存放的都是数值
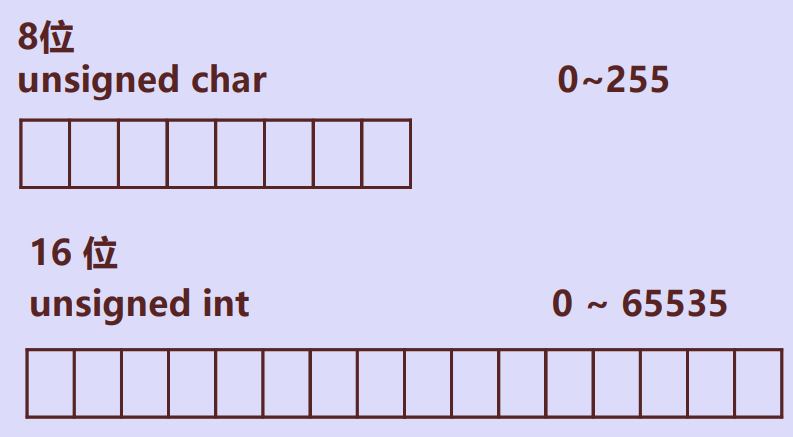
有符号数

有符号机器数的编码形式
定点机器数和真值

小数的机器数忽略小数点左边的部分
所有机器数最左位都是代表正负1和0
原码表示法

1.原码的定义
整数原码

小数原码

例一:已知原码求真值

例二:已知真值求原码

2.原码表示法总结

定点数的补码表示法
一、补码表示法
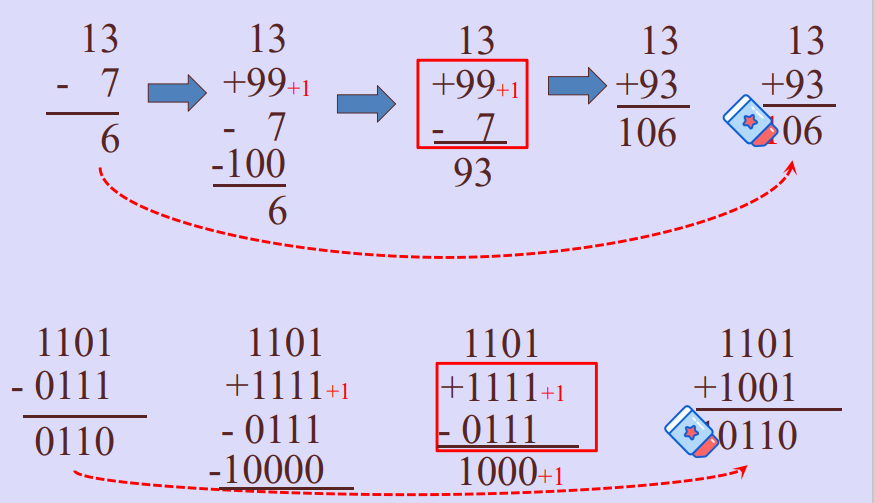
结论:
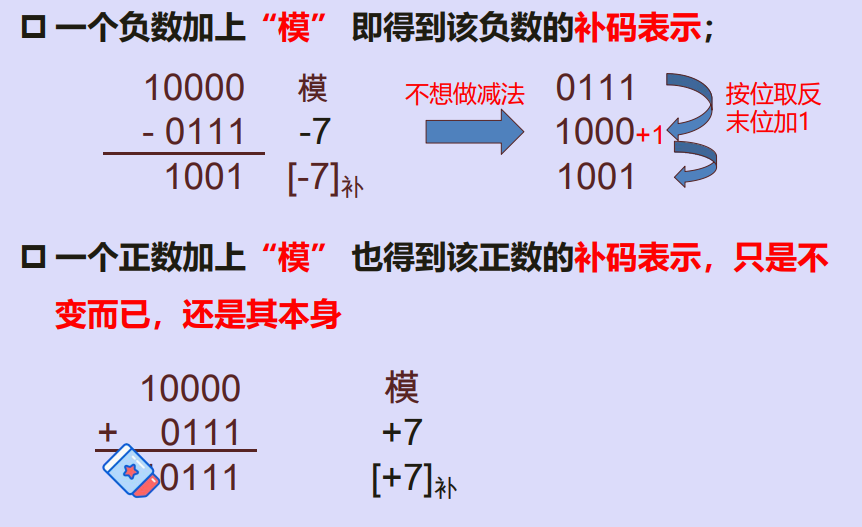
二、补码定义
整数

小数

三、求补码表示的方法

例一:已知小数补码求真值

例二:已知整数补码求真值

例三:已知负数补码求真值

证明:已知[y]补,求[-y]补

求补的应用:把所有减法变加法

例四:几个特殊值的机器值
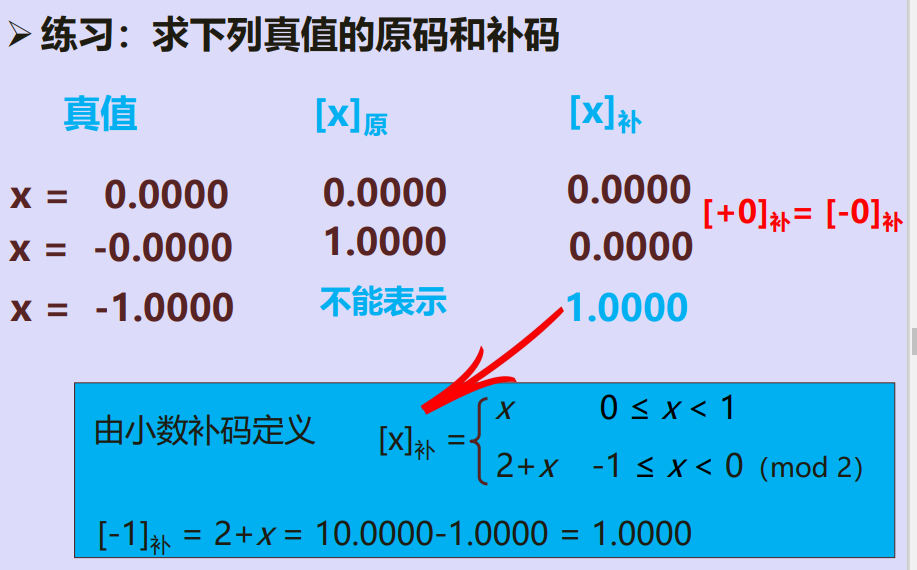
四、反码的表示法
整数

小数

例一:已知整数反码求真值

例二:求0的反码

总结:三种机器数

各种机器数的数值表示(机器字长8位)
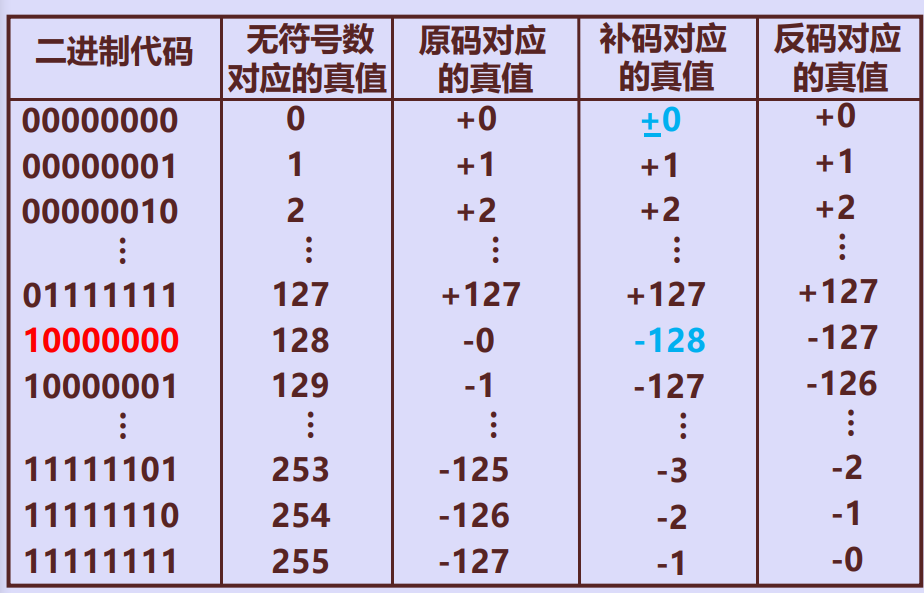
定点数加减法
一、补码加减运算公式

例题1:加法

例题2:减法

第4讲:定点数加减法器实现
一、1-bit加法器
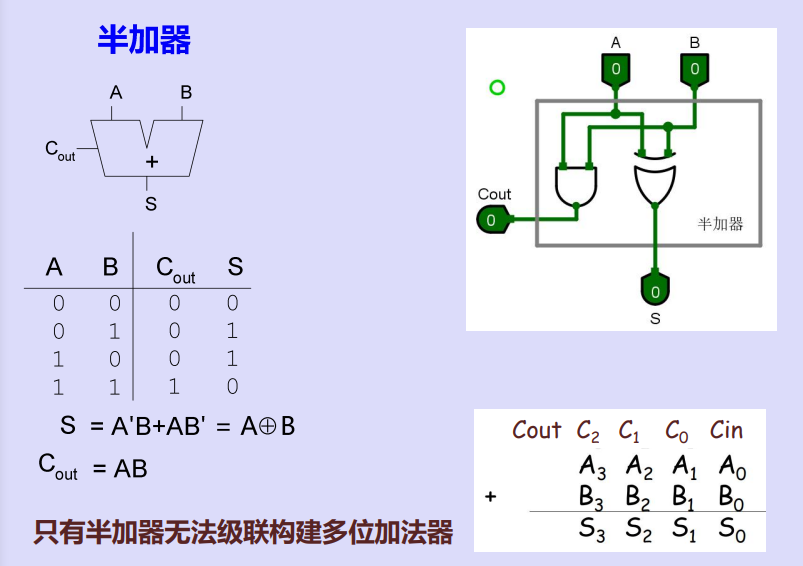
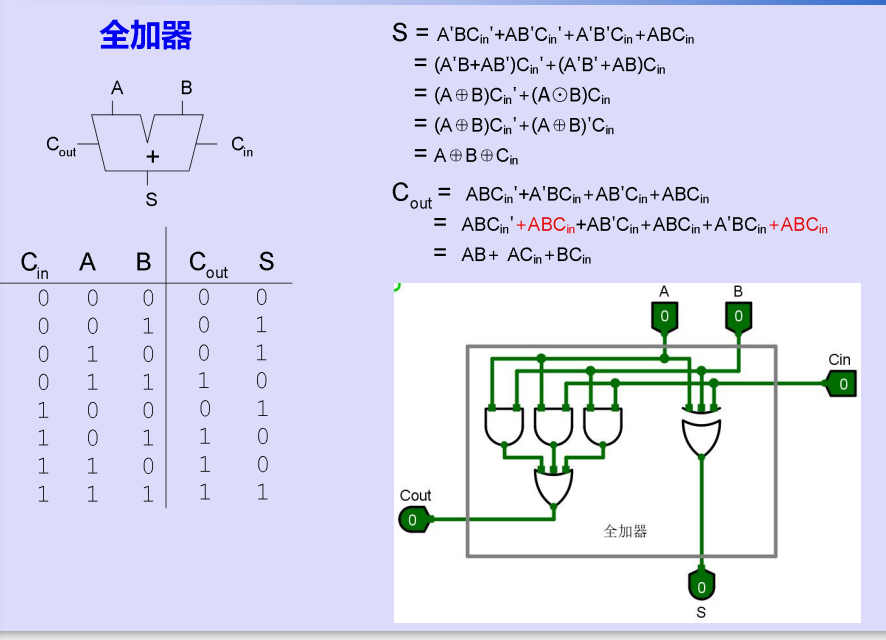
二、n-bit加法器
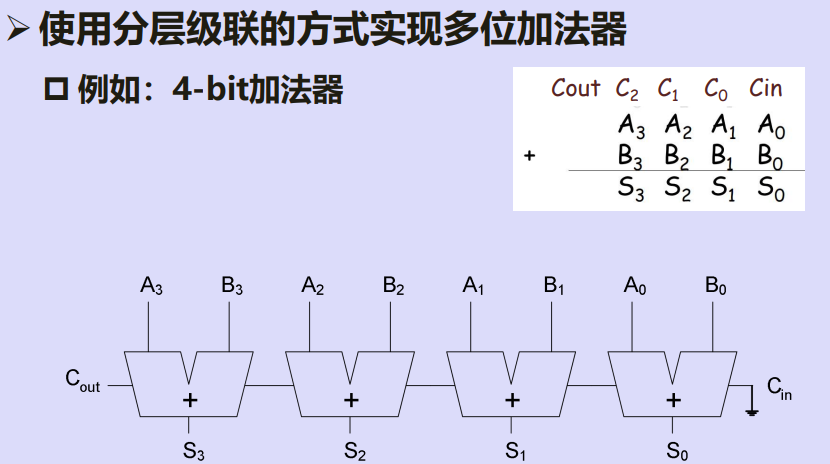
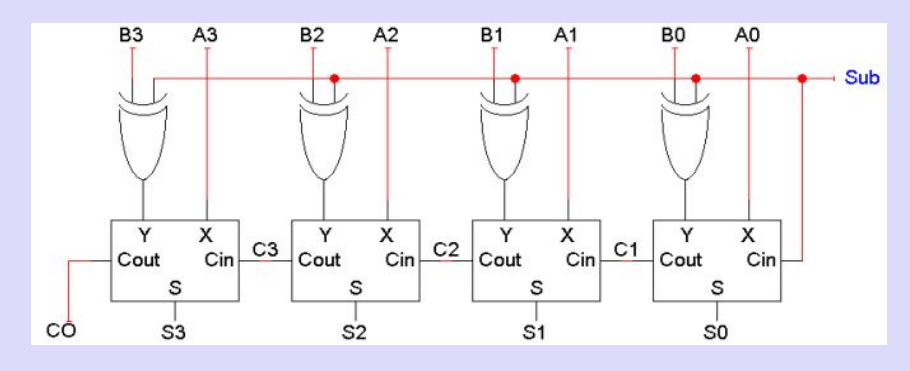
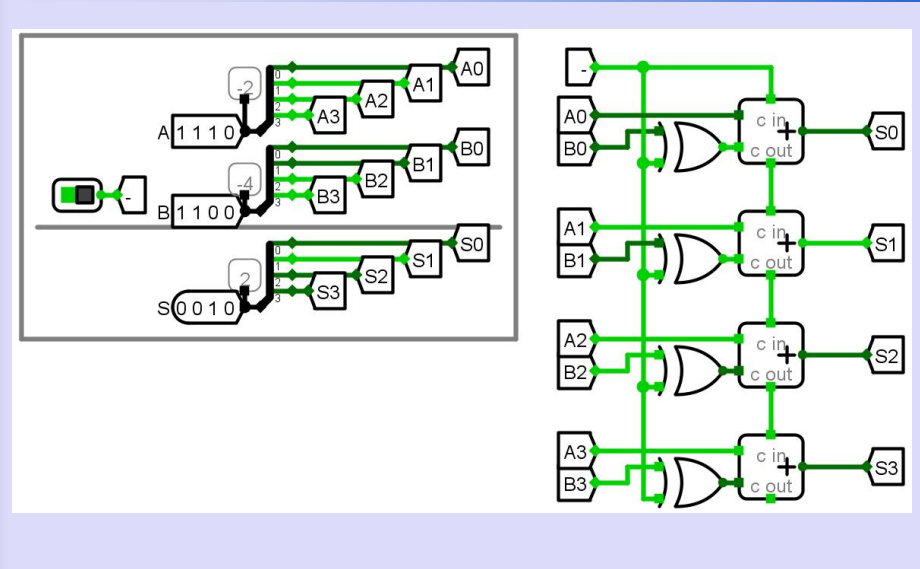
n-bit减法器
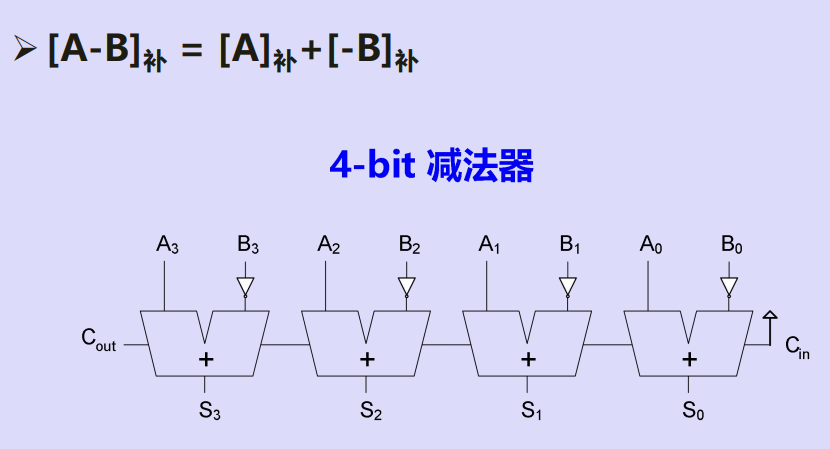
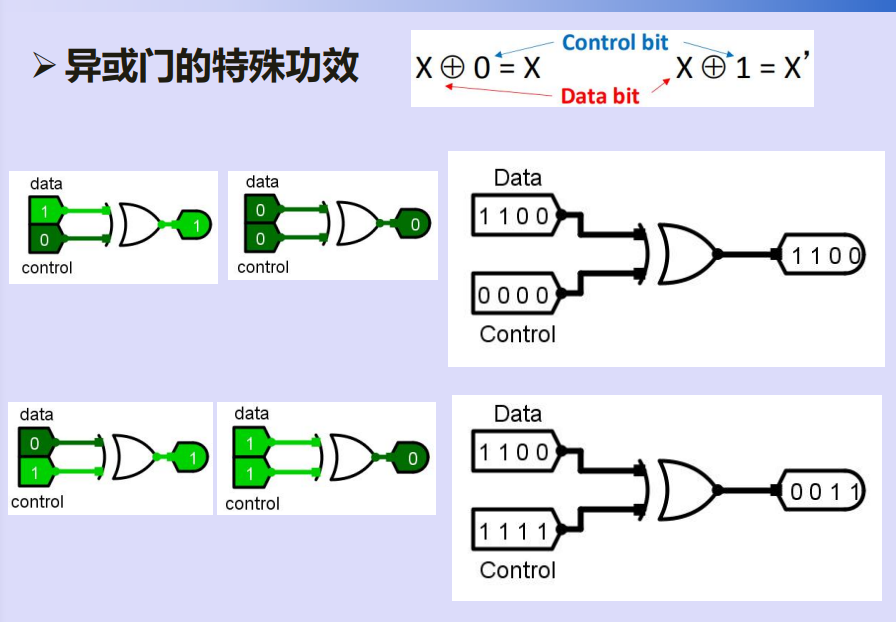
三、加减法器
定点数加减法的溢出判断
一、溢出问题(练习1)

练习2

2038年问题

二、溢出概念


三、溢出判断
1.一位符号位判断溢出

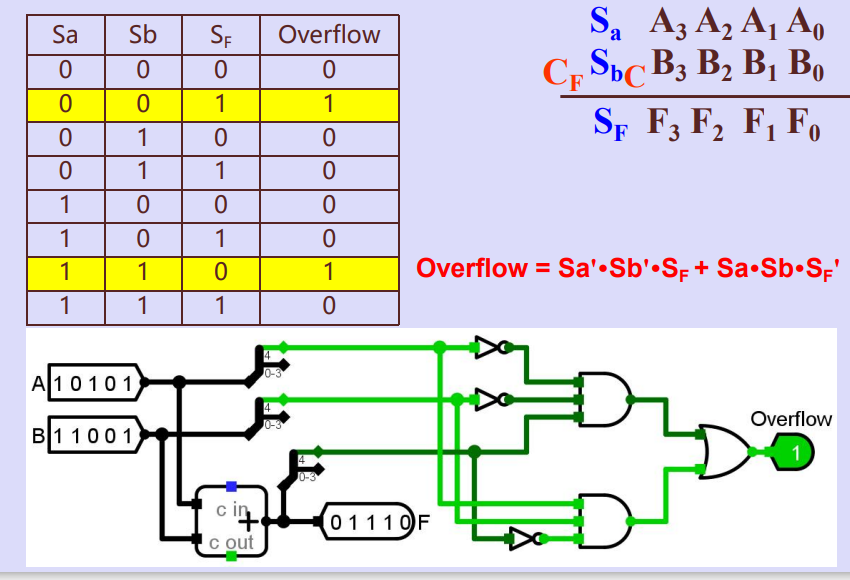
2.符号位进位CF和最高有效位C进位判断溢出

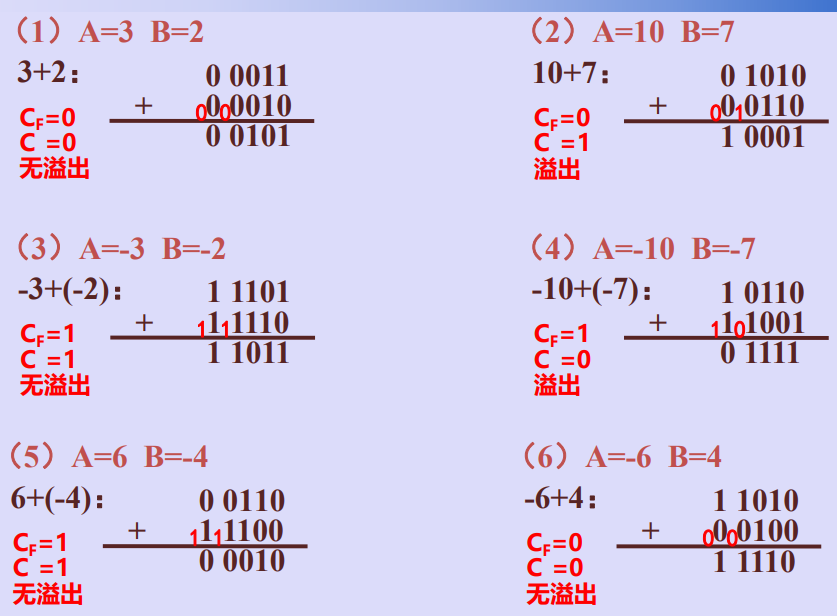
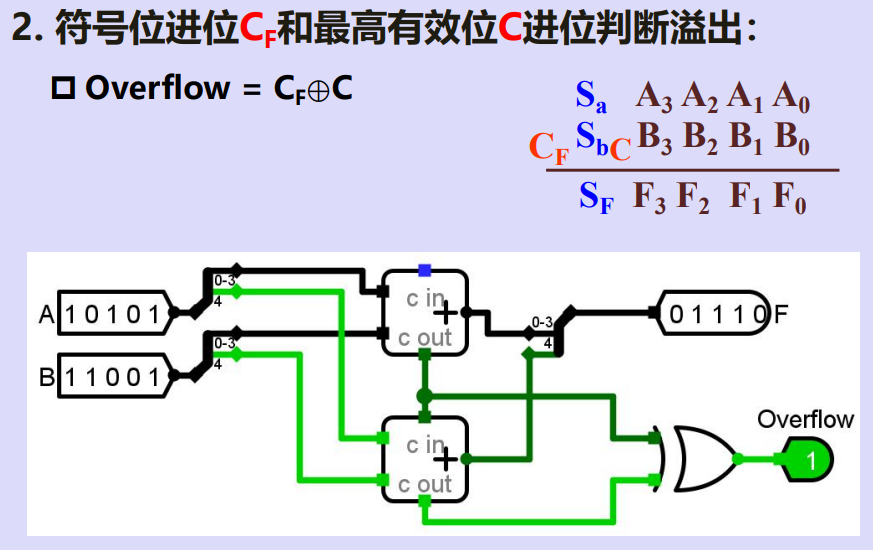
3.双符号位判断溢出

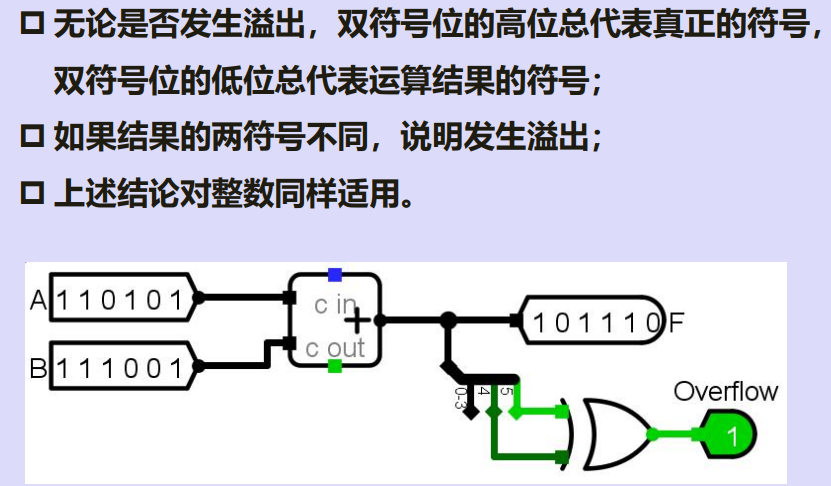
总结:补码加减法硬件电路
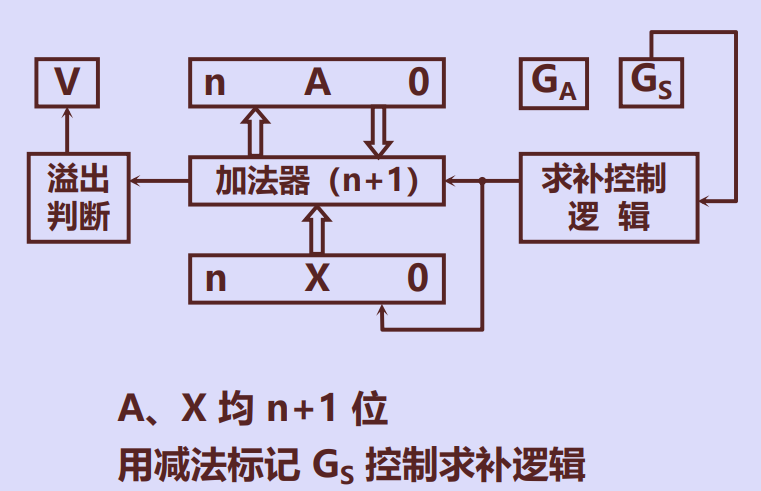
定点数移位运算
一、移位运算意思

二、算术移位和逻辑移位

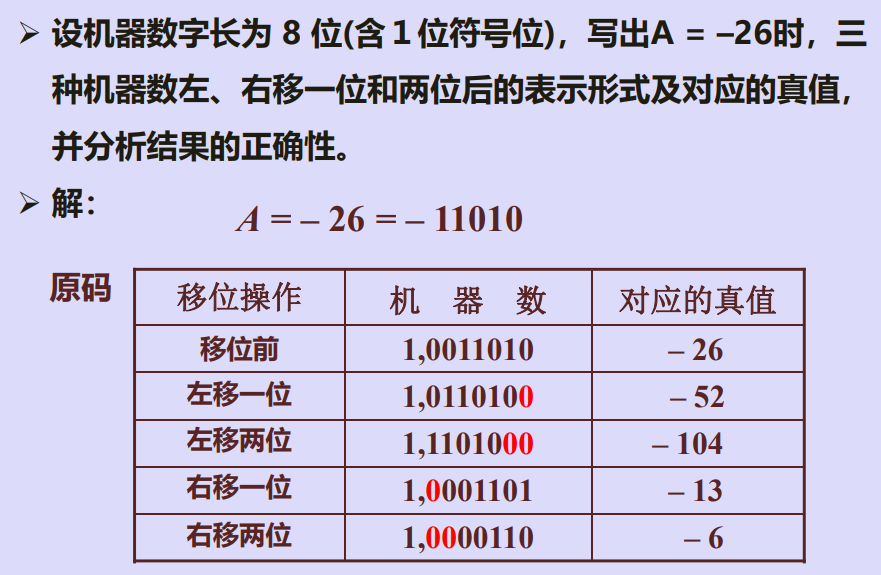
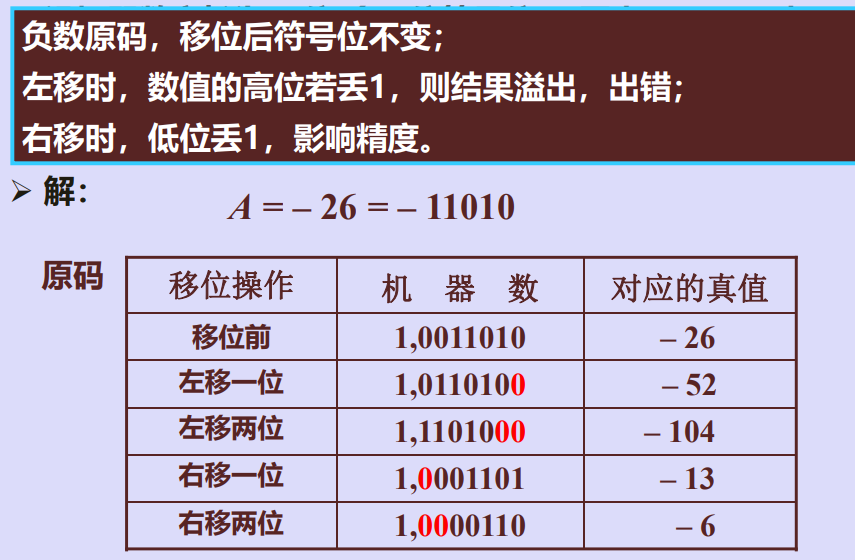
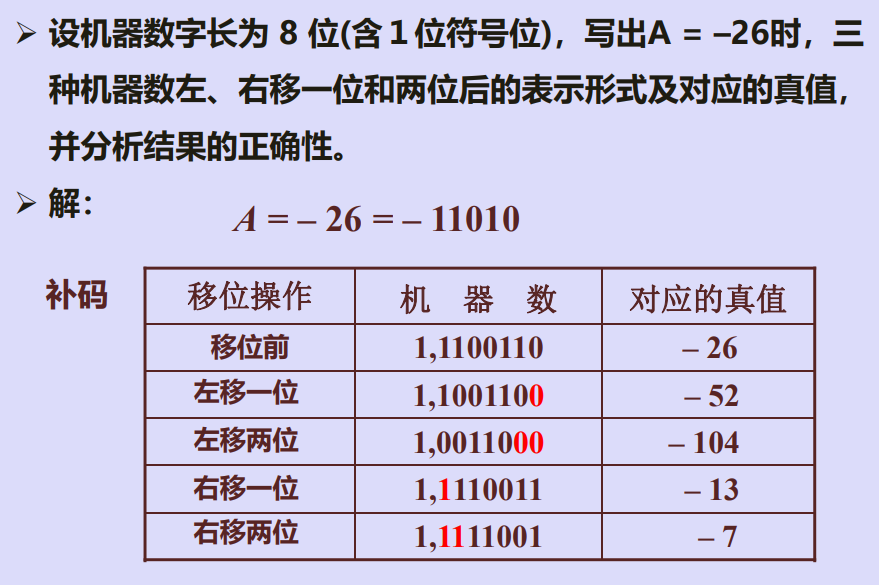
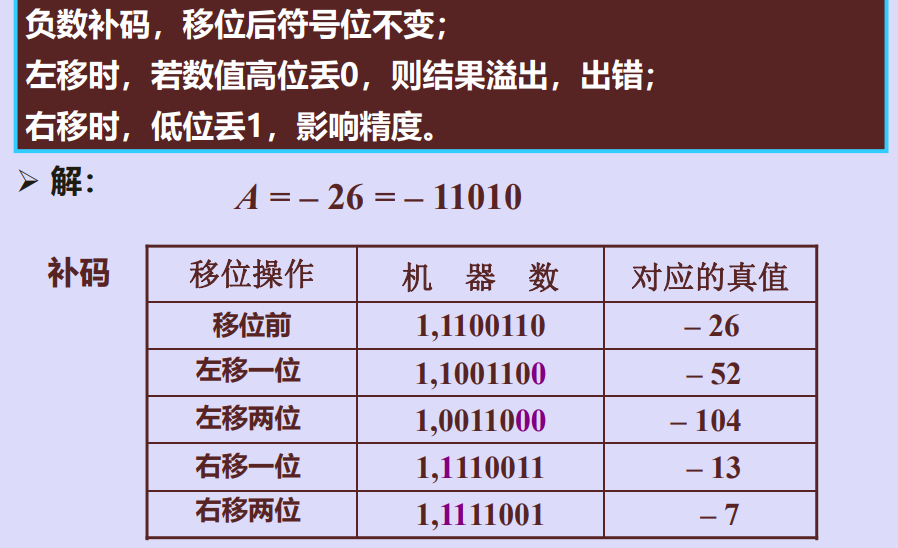
三、算术移位(有符号数移位)规则
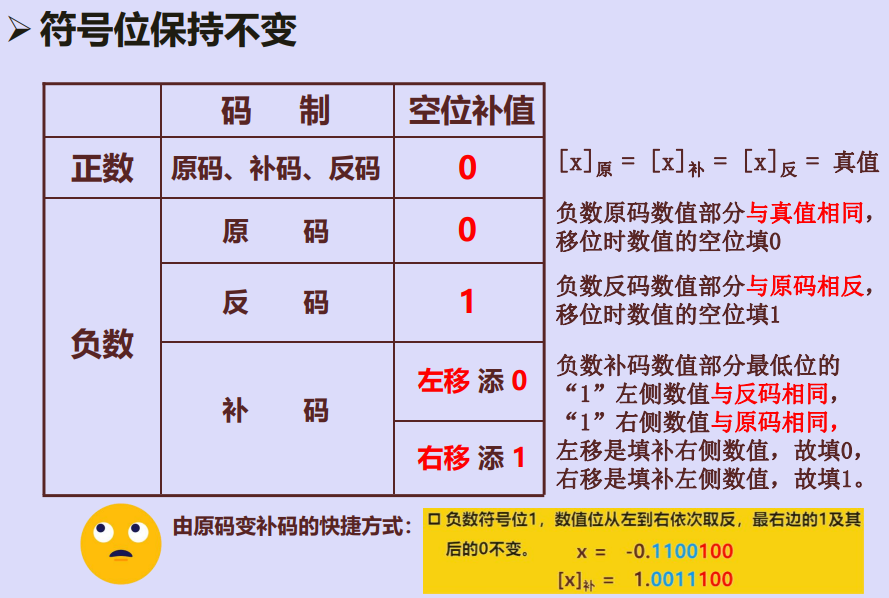
例1
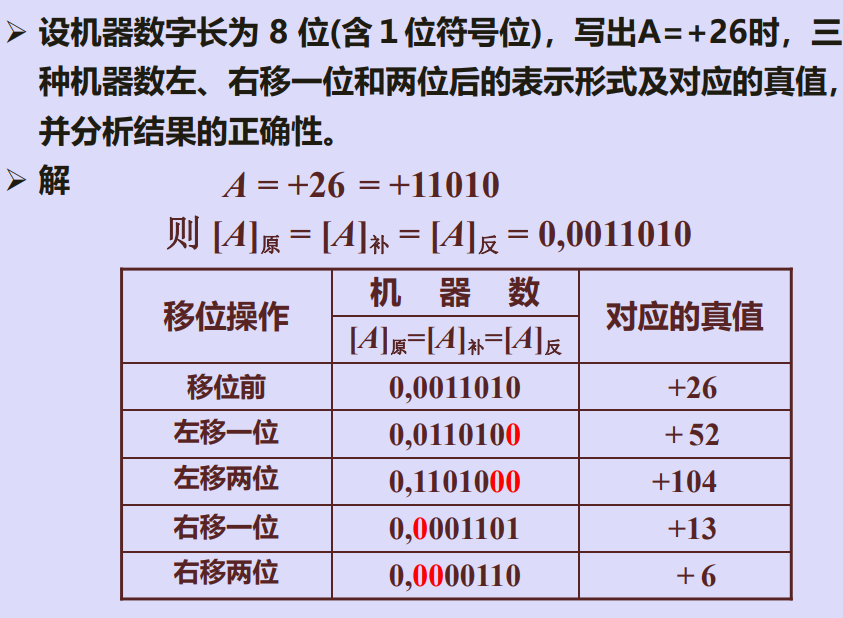
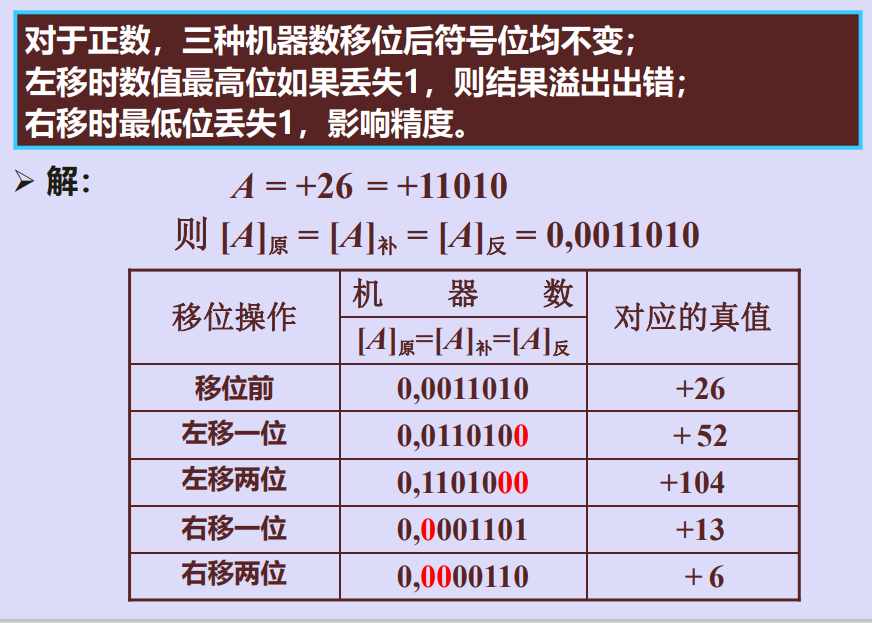
例2
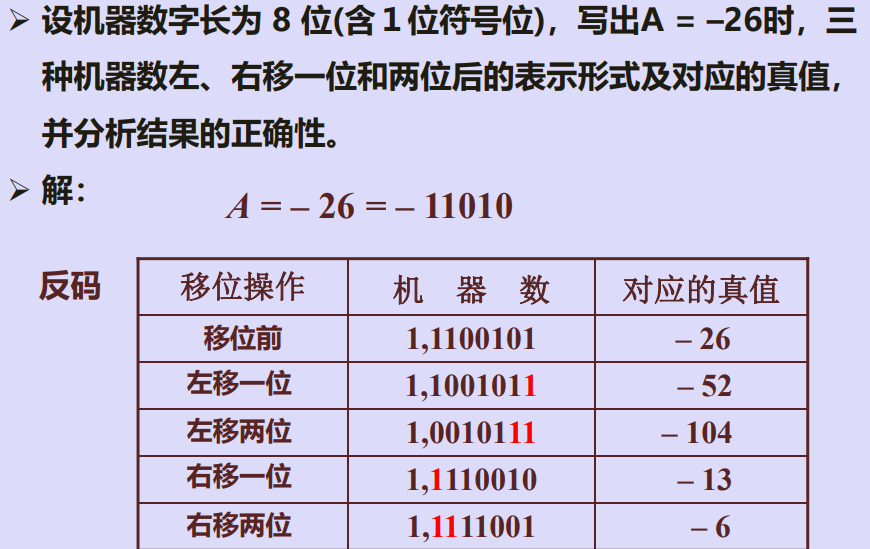
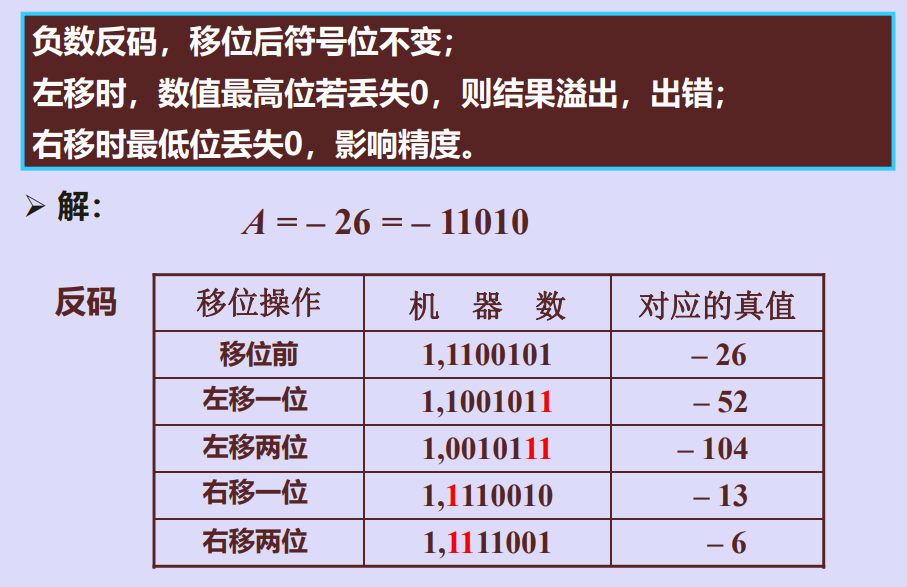
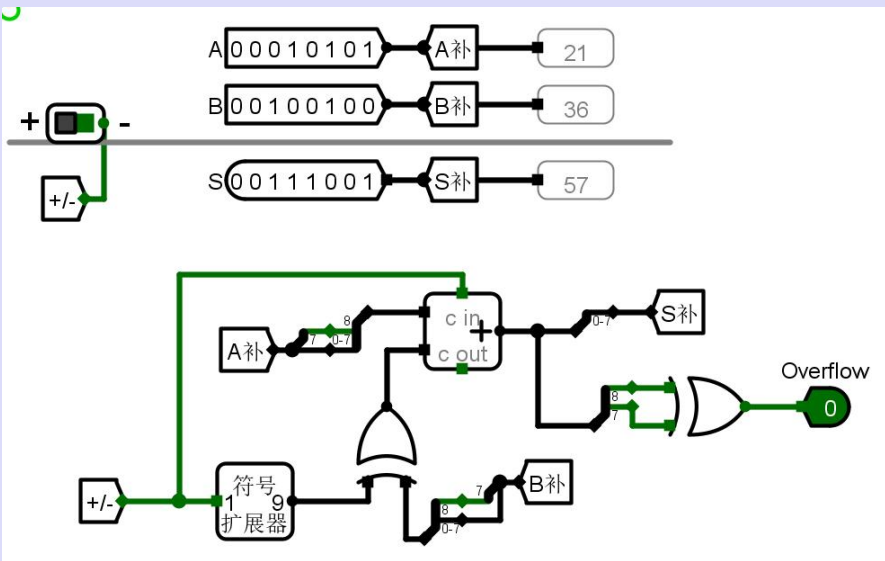
四、移位运算硬件实现
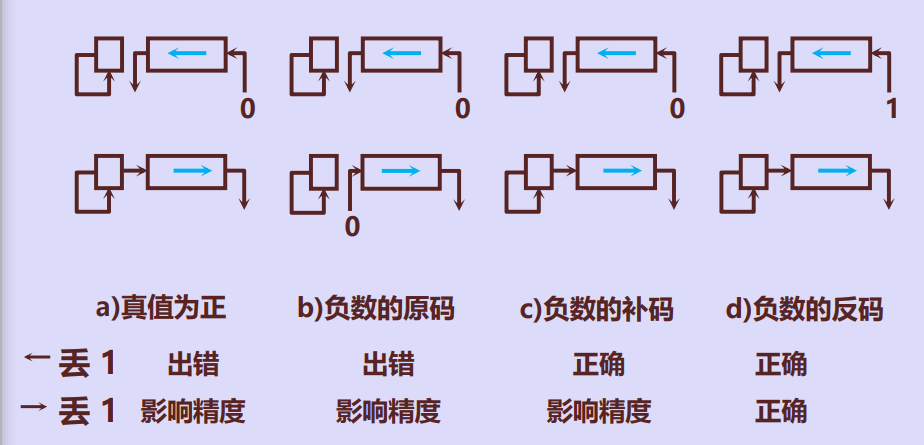
第5讲 计算方法-定点数算术逻辑单元
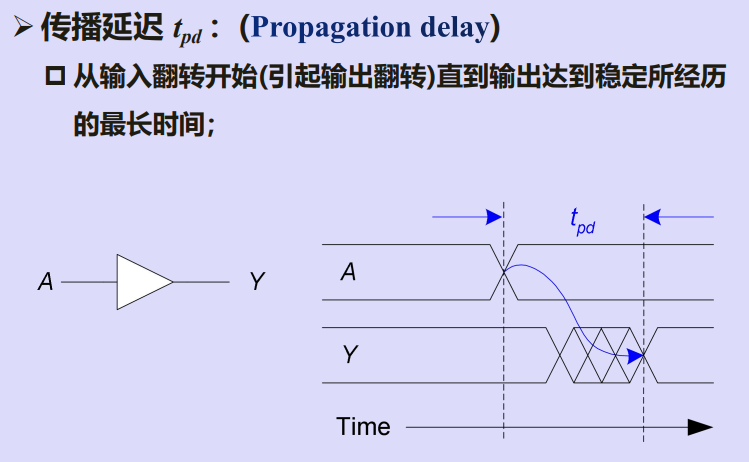
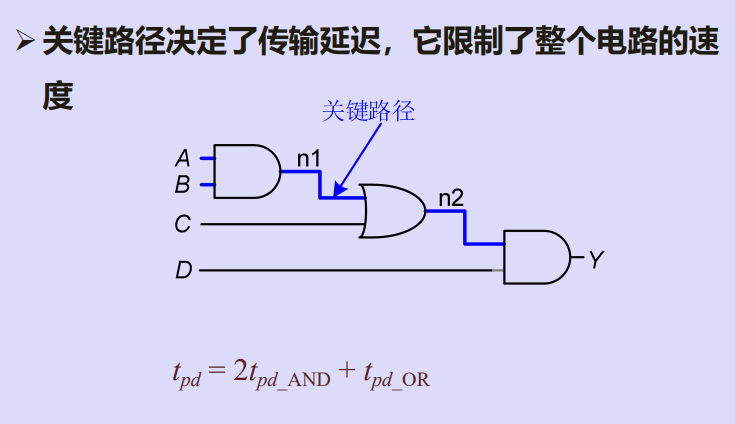
一、串行进位加法器的延迟问题
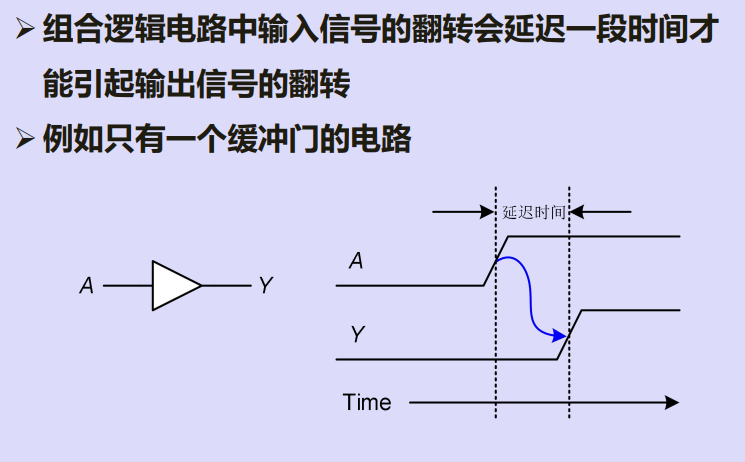
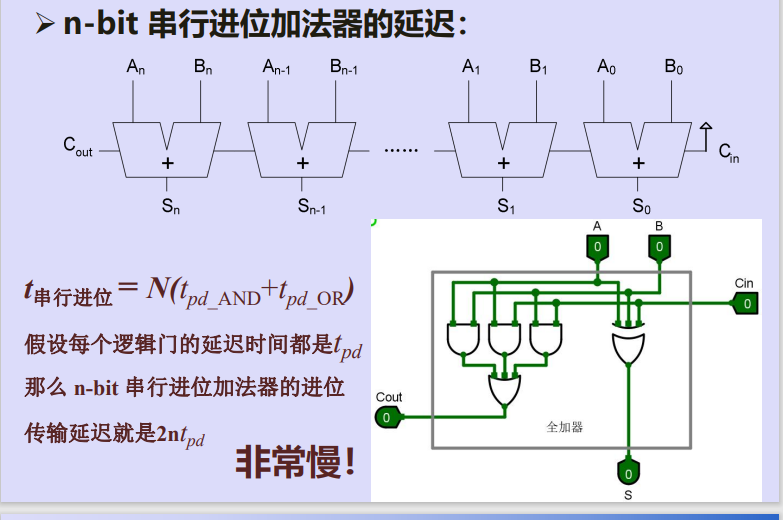
二、分析n-bit串行加法器的进位




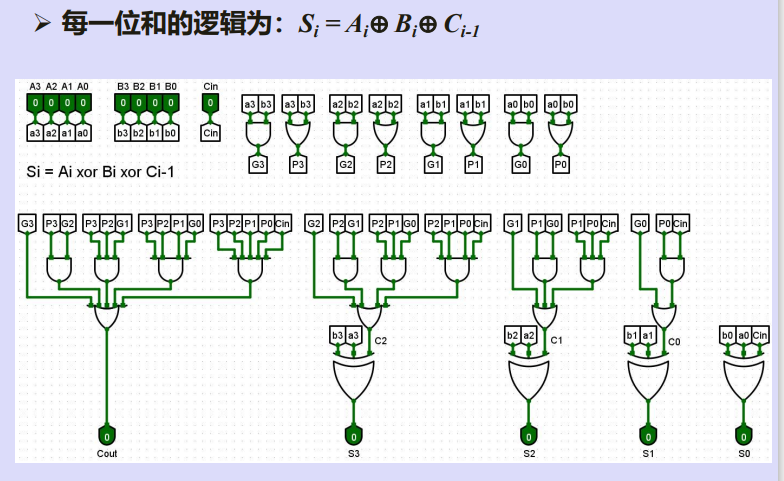
三、4-bit先行进位电路
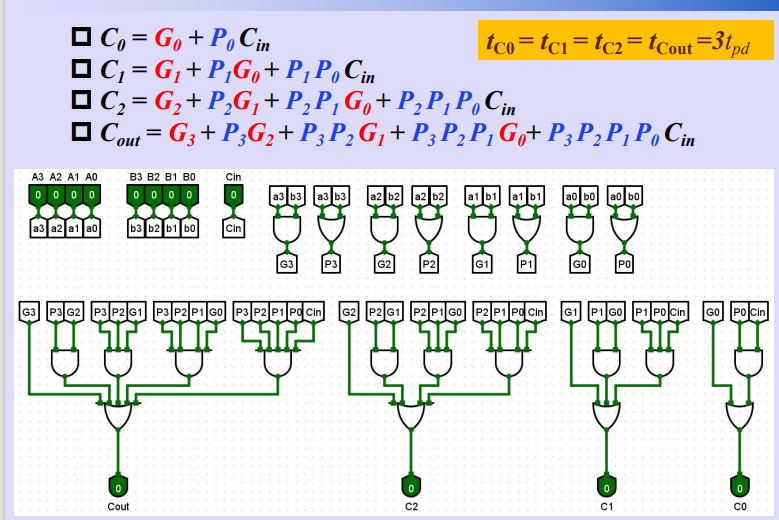
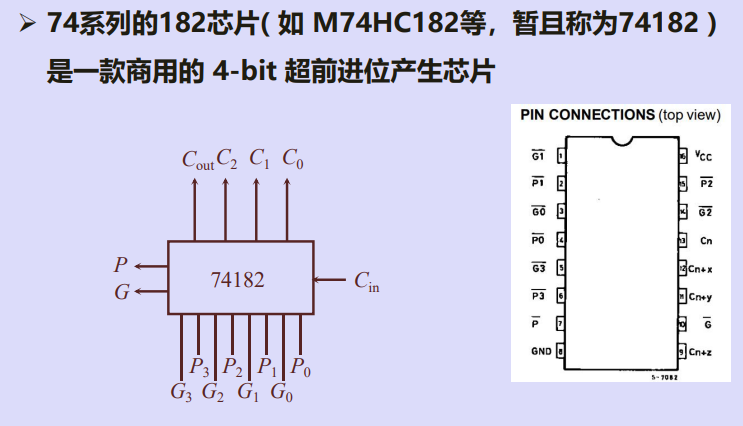
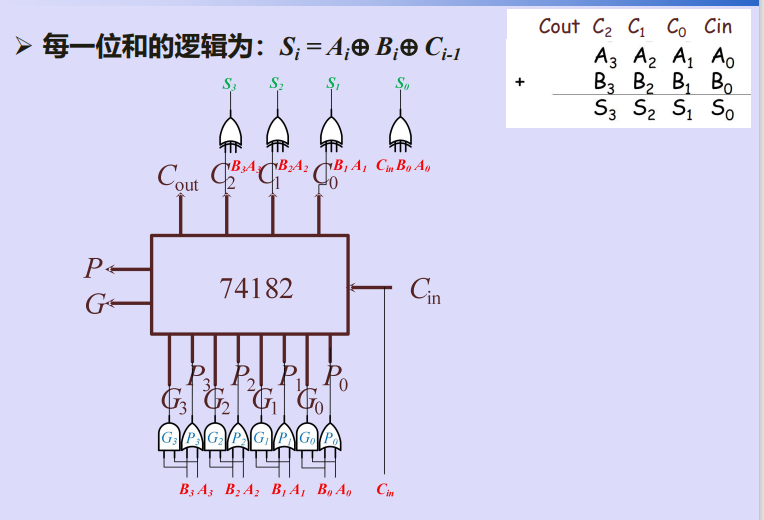
四、4-bit超前进位加法器
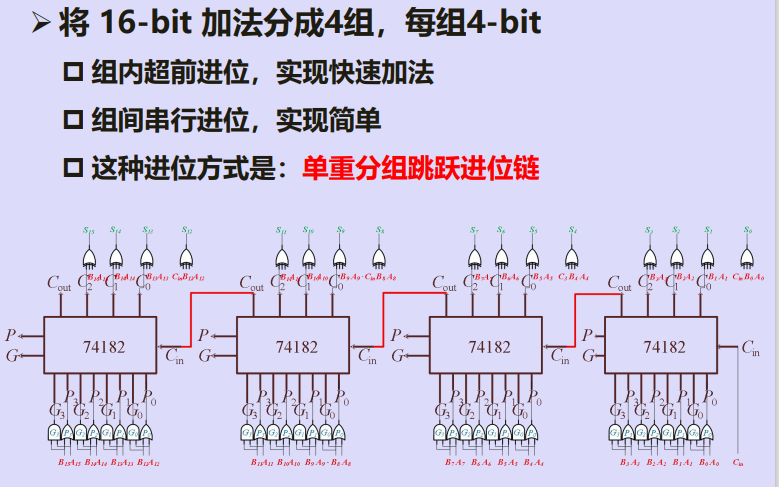
五、16-bit快速加法器
六、16-bit更快速加法器

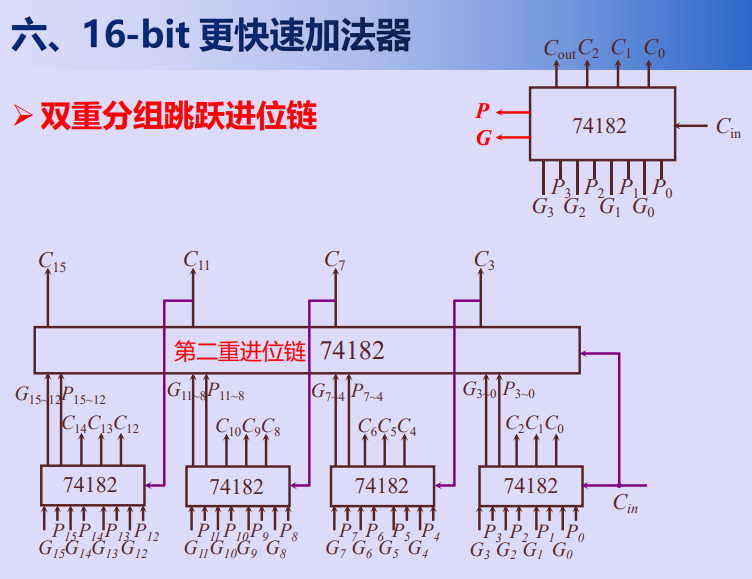
算术逻辑单元
一、算术逻辑单元概念
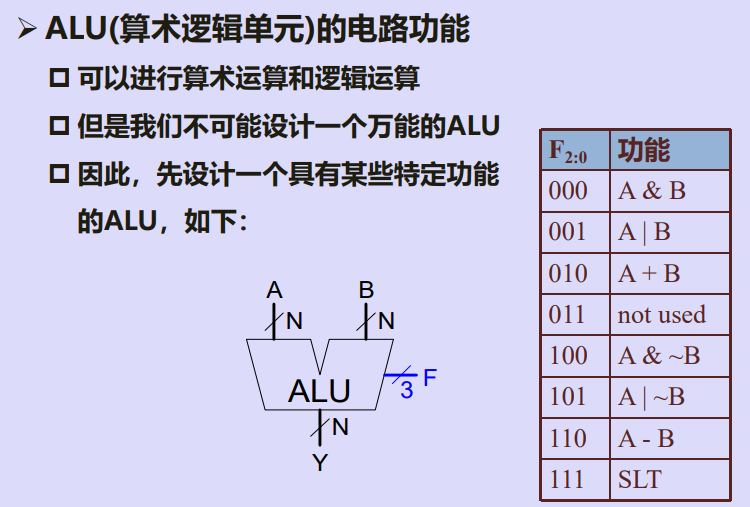
二、设计一个特定功能的算术逻辑单元
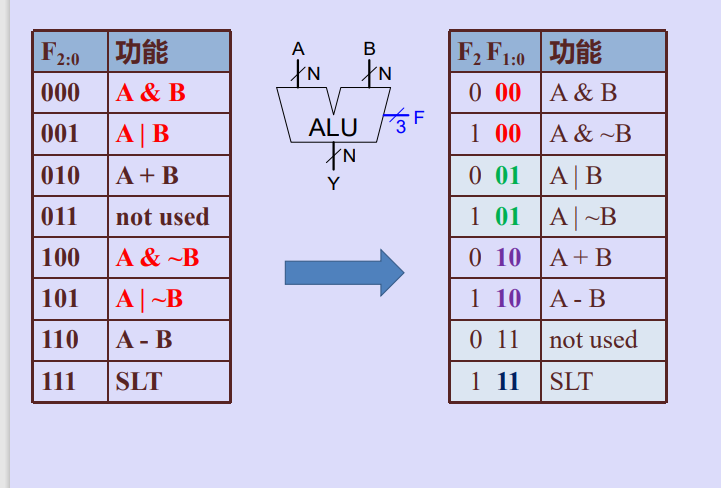

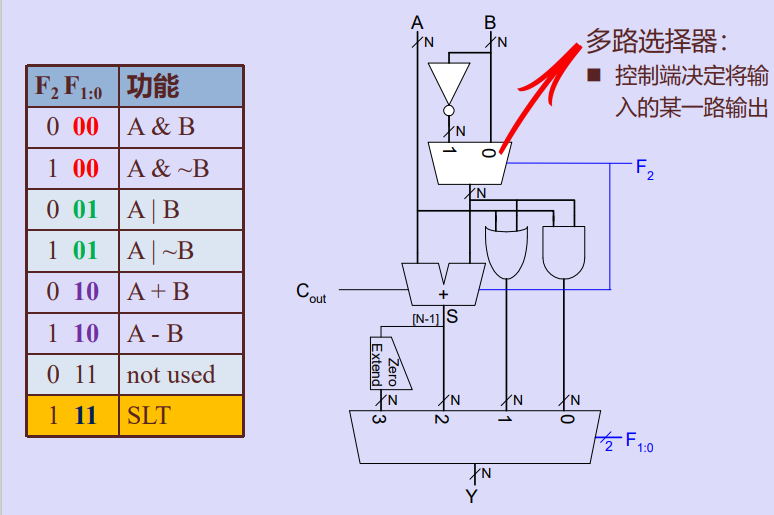
三、一款商用算术逻辑单元芯片74181
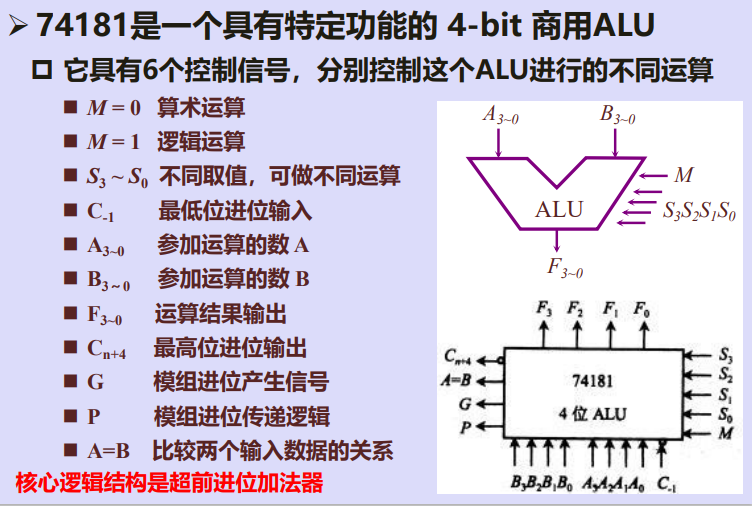
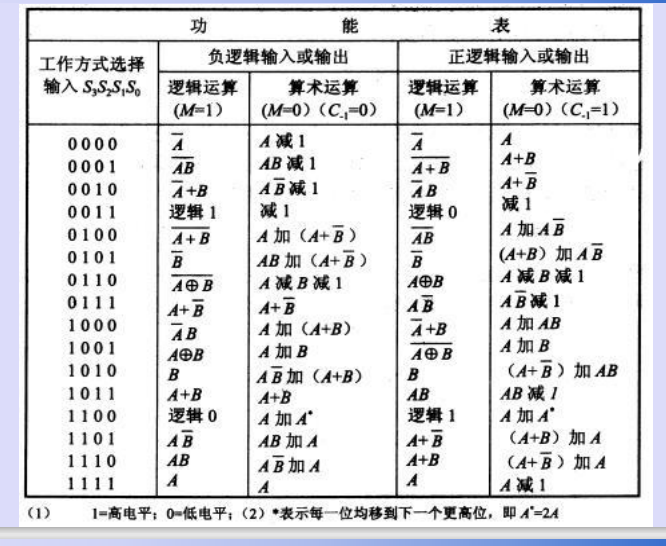
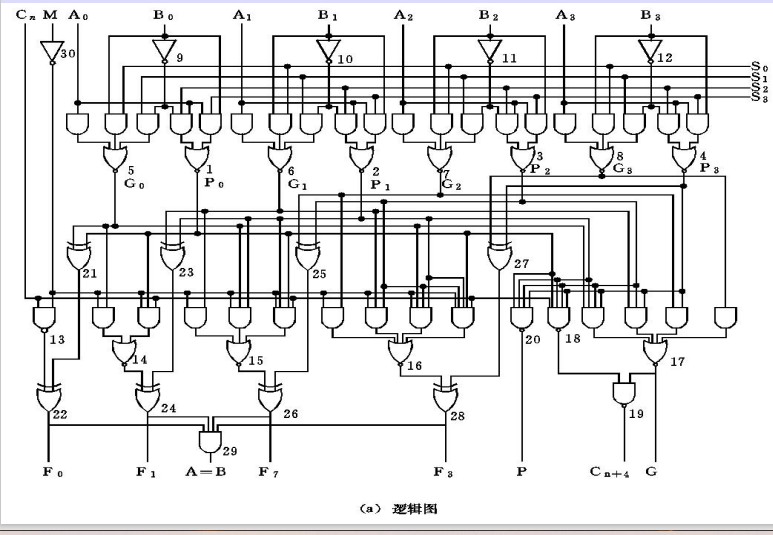
四、多位ALU
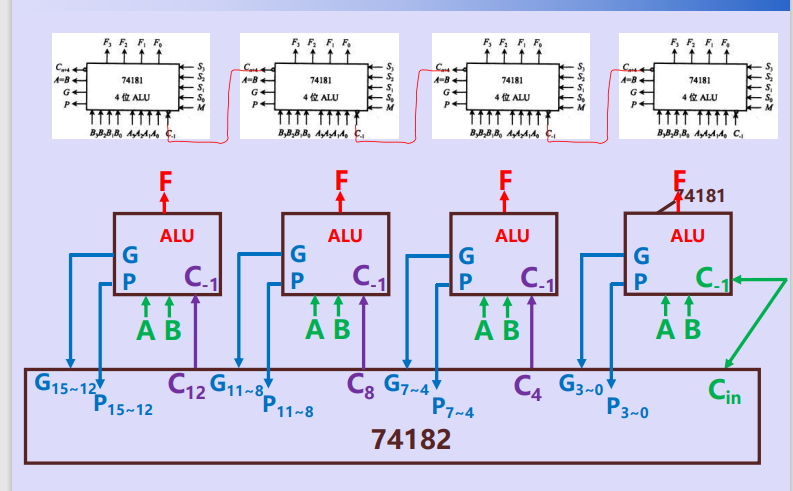
第9讲 存储器存储结构
半导体存储器概述
一、按存储器分类


EPROM

Flash存储器


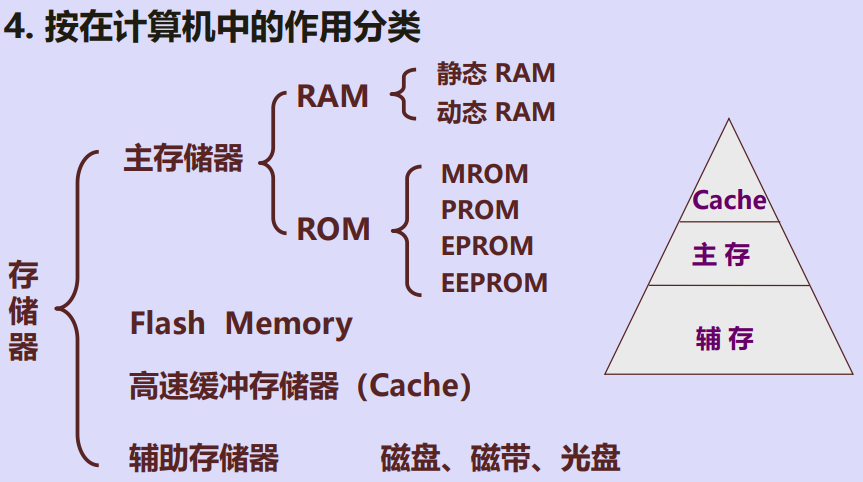
二、存储器的层次结构
1. 存储器各层位置及特点
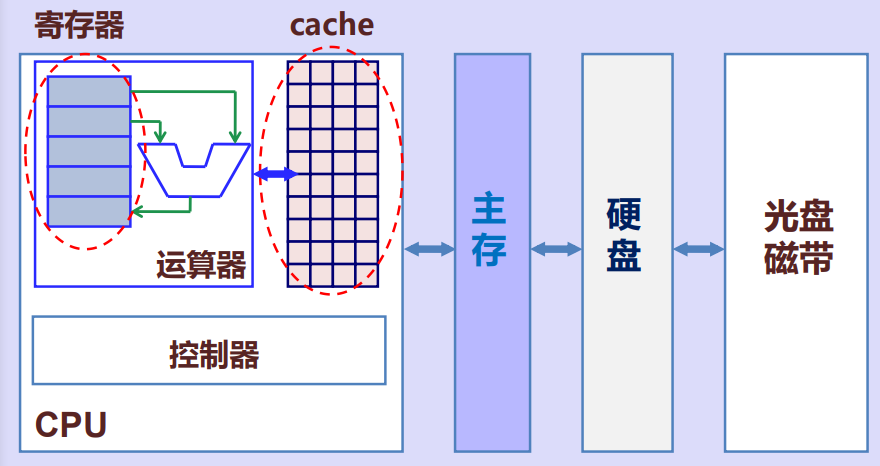

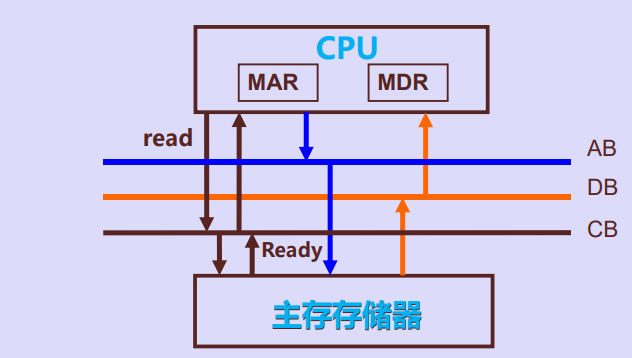
三、主存和cpu的联系
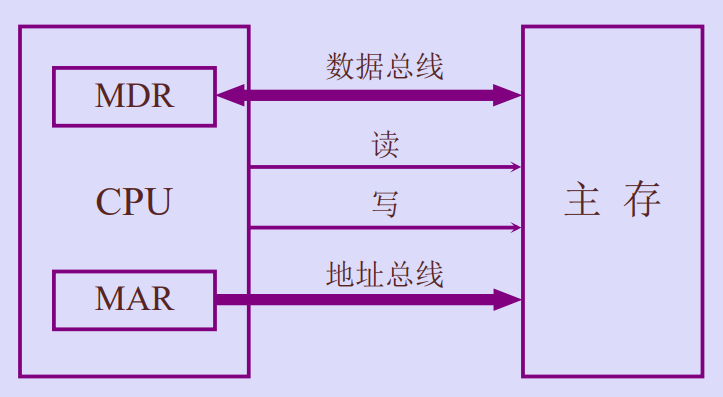
读操作
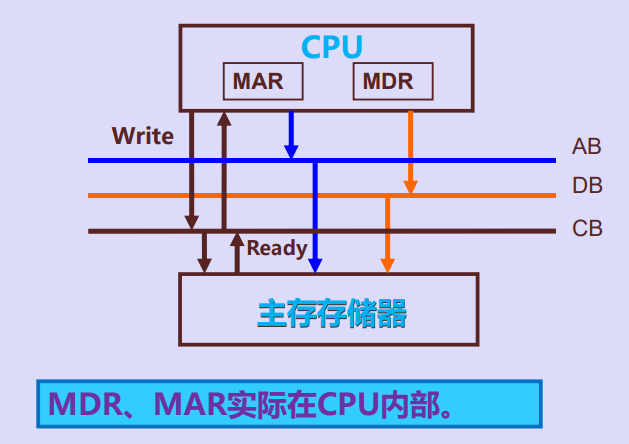
写操作
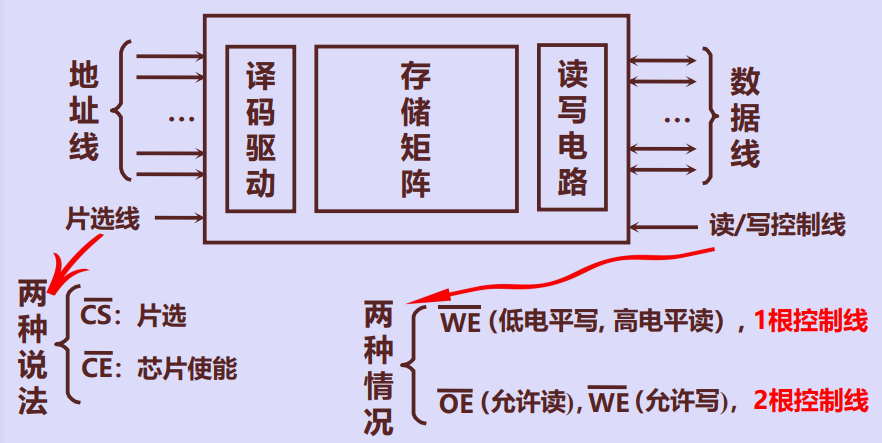
四、半导体存储芯片的基本结构
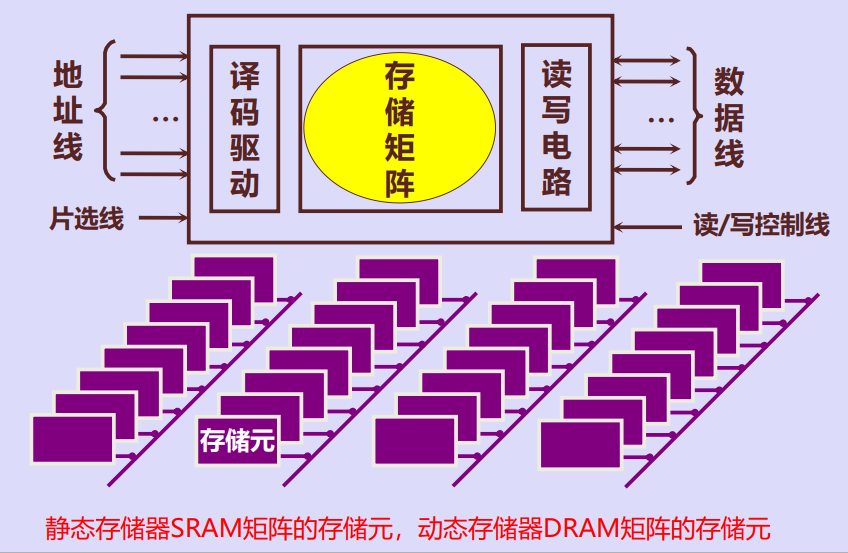
静态随机存储器的存储元
静态随机存储器基本单元电路(存储元)
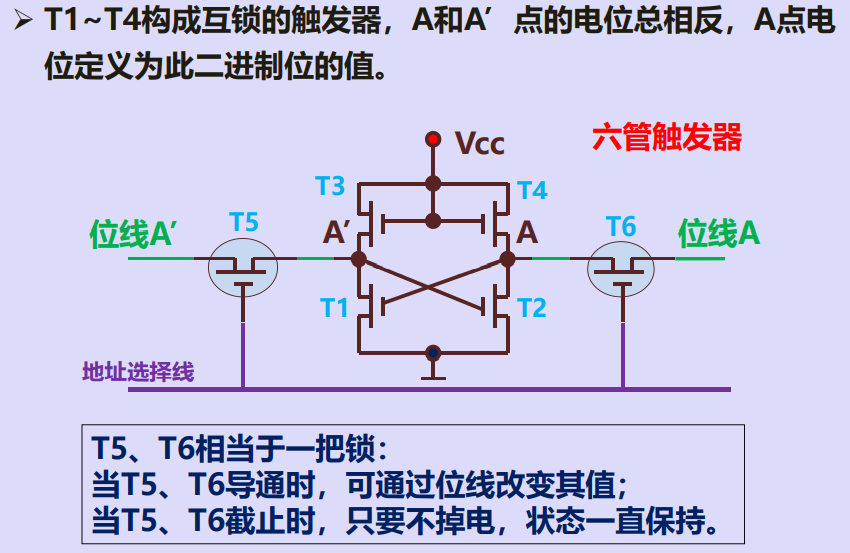
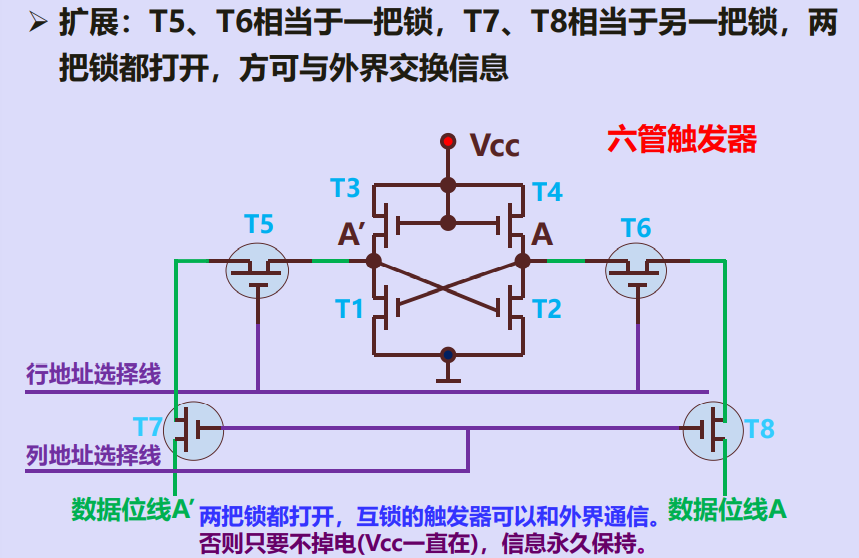
静态存储元的读操作
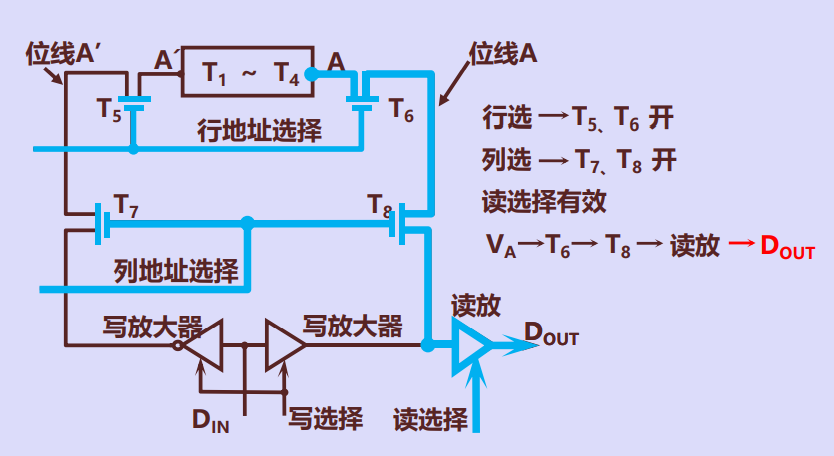
静态存储元的写操作
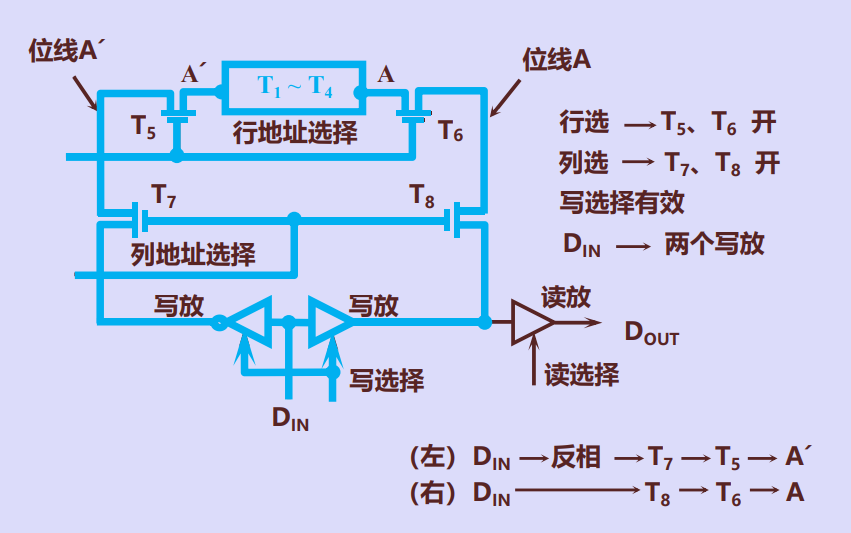
静态储存元的抽象表示
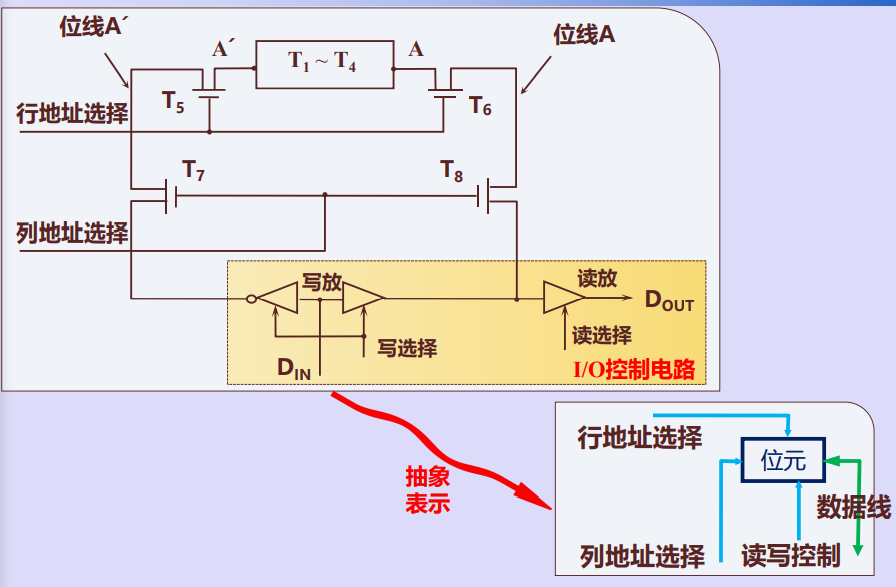
动态随机存储器的存储元
动态随机存储器基本单元电路
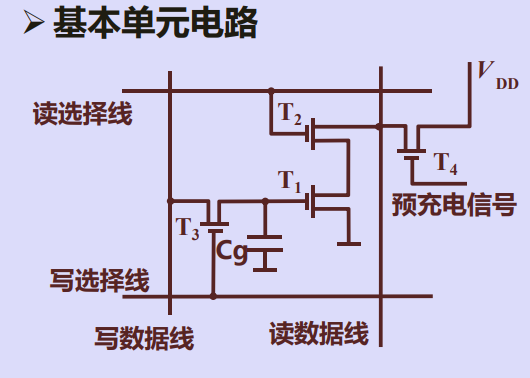
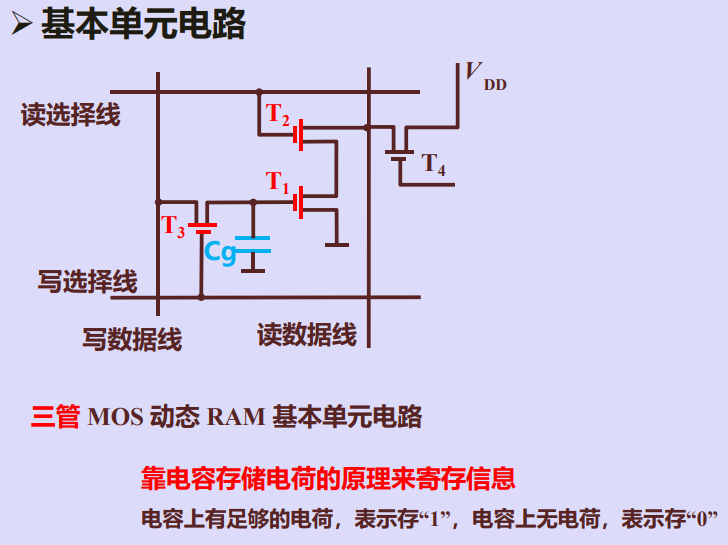
存储元读过程
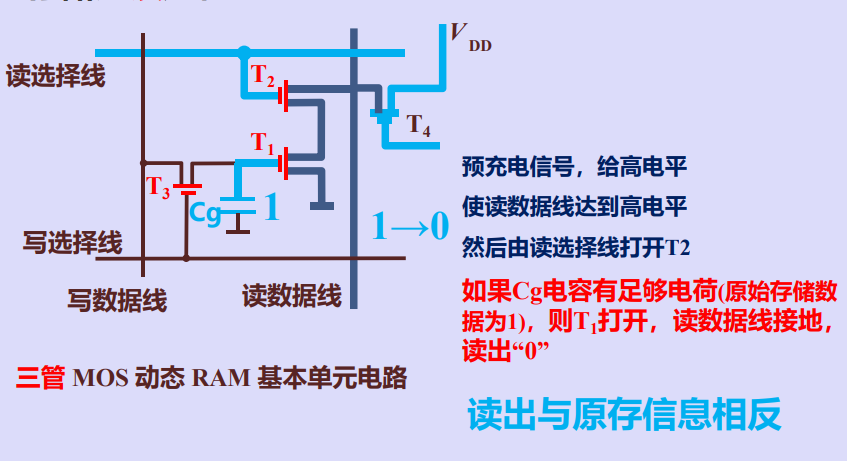
存储元写过程
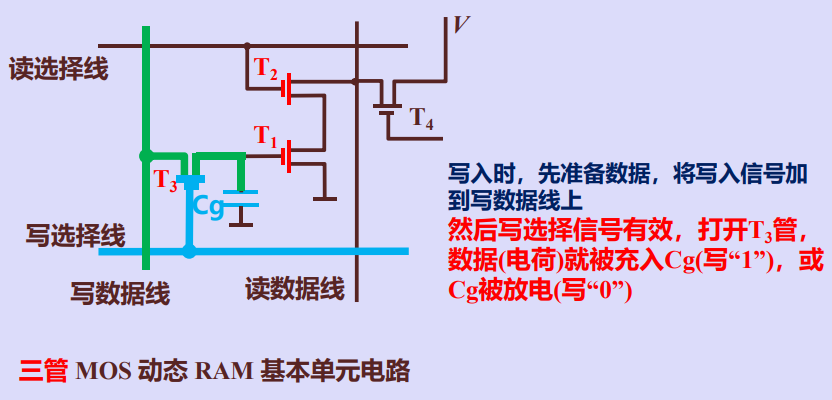
动态存储元简化
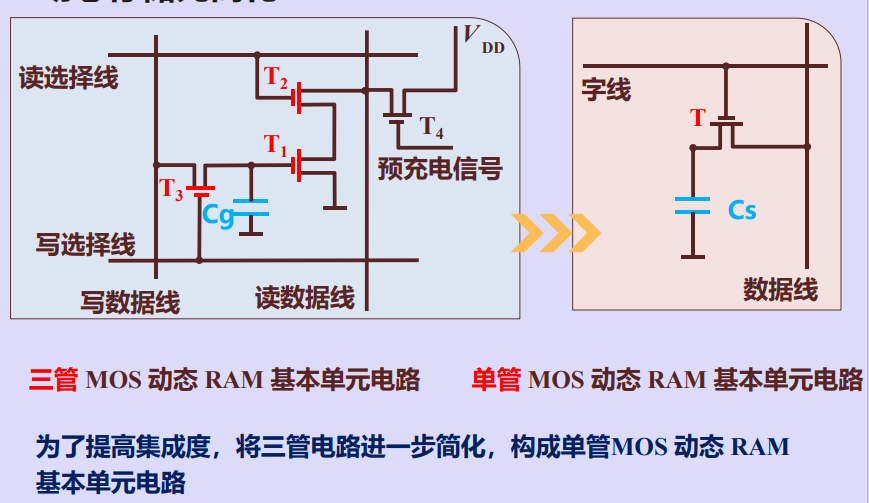
单管动态存储元



动态存储元的抽象
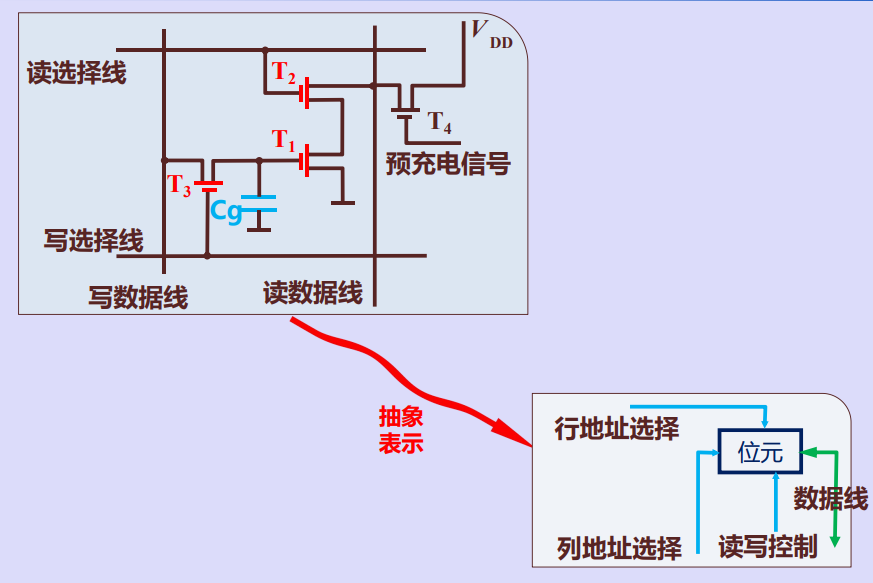
随机存储器的存储字结构
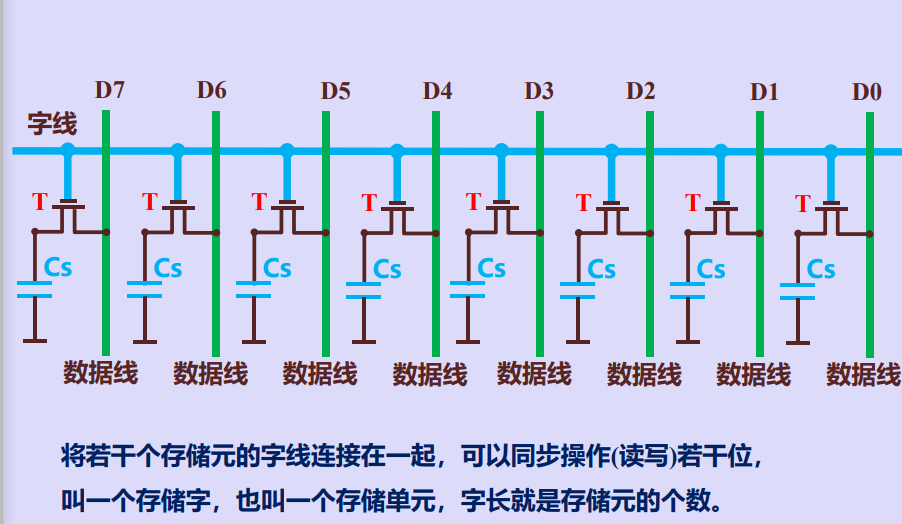
四、半导体存储芯片的基本结构
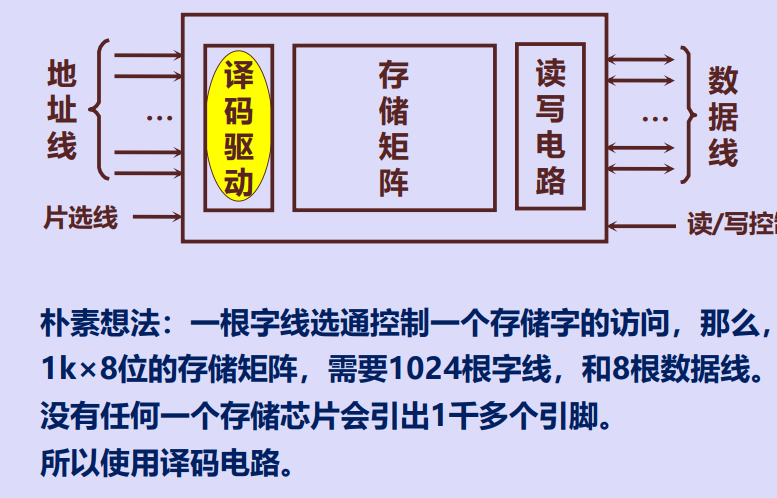
译码器&编码器
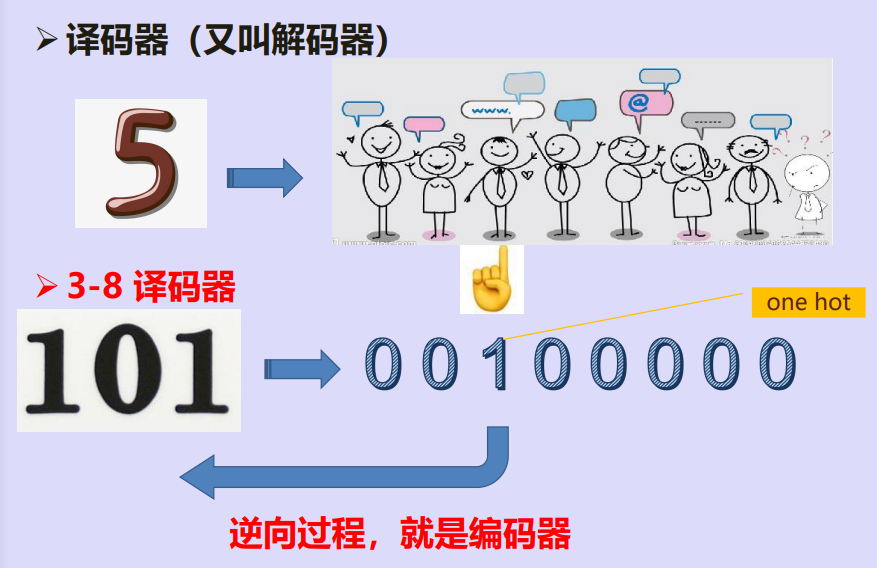
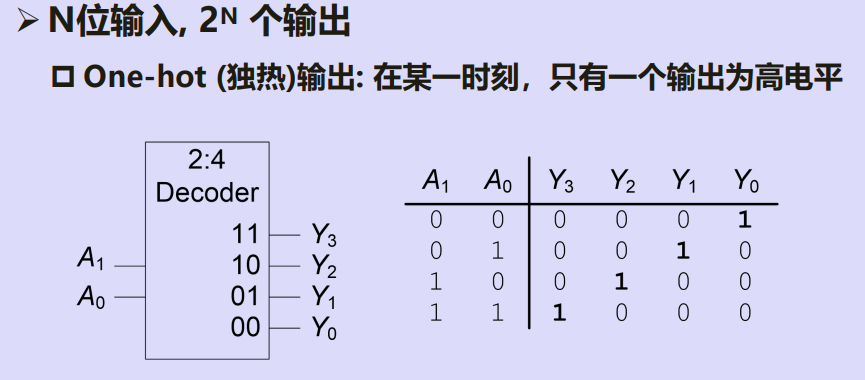
译码器(解码器)
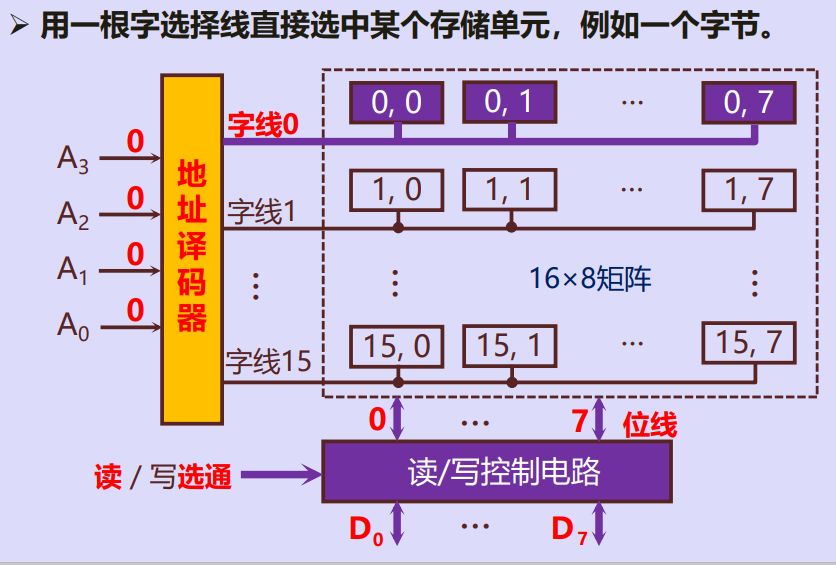
半导体储存芯片的译码驱动
(1)线选法
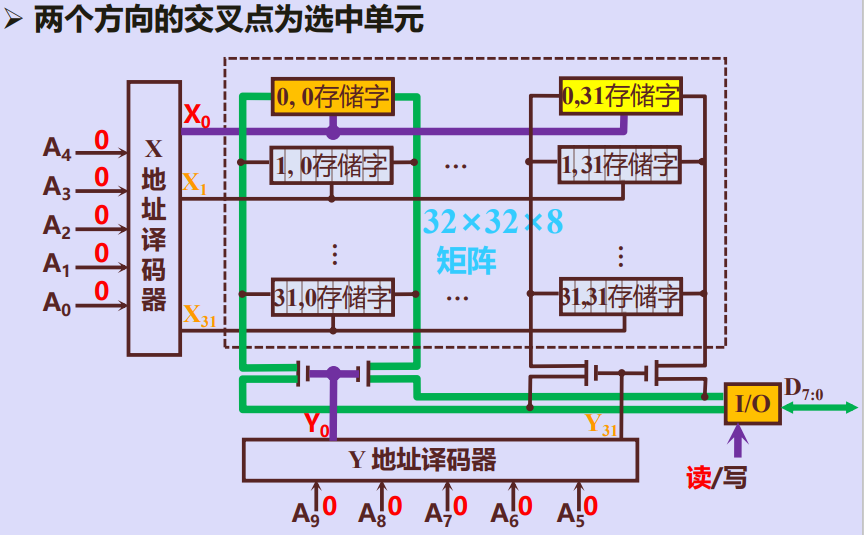
(2)重合法
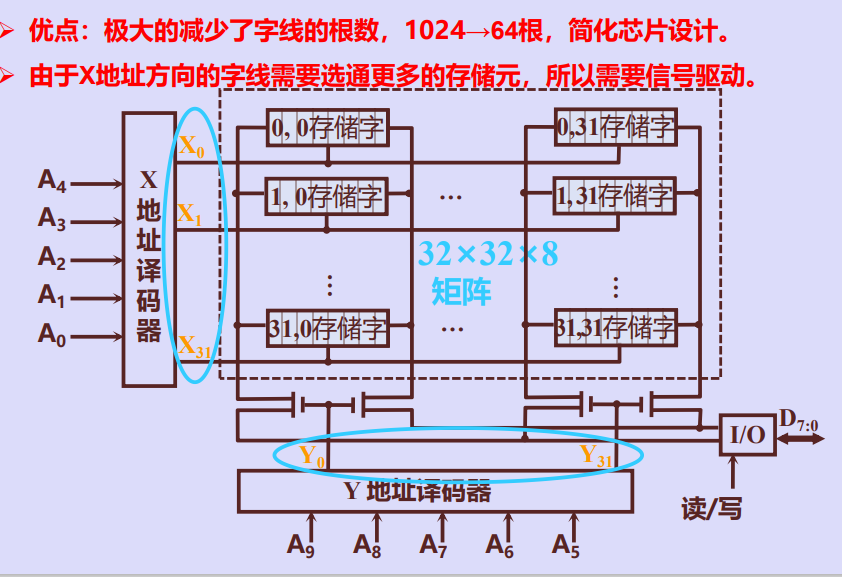
优点
-YzQa8FUw-1684843776904)]
单管动态存储元
[外链图片转存中…(img-Q5lbJCfq-1684843776905)]
[外链图片转存中…(img-SJtDzSUD-1684843776905)]
[外链图片转存中…(img-C1Mf85jv-1684843776906)]
动态存储元的抽象
[外链图片转存中…(img-ck4xnTzY-1684843776906)]
随机存储器的存储字结构
[外链图片转存中…(img-FMtnoPD3-1684843776906)]
四、半导体存储芯片的基本结构
[外链图片转存中…(img-HIDDudQQ-1684843776907)]
译码器&编码器
[外链图片转存中…(img-xuQHX8ai-1684843776907)]
译码器(解码器)
[外链图片转存中…(img-UlDjJASB-1684843776908)]
半导体储存芯片的译码驱动
(1)线选法
[外链图片转存中…(img-UZDZ3F6Q-1684843776908)]
(2)重合法
[外链图片转存中…(img-PqpqsD8x-1684843776908)]
优点
[外链图片转存中…(img-jeYsyAP9-1684843776909)]

![[VRTK4.0]设置OpenXRCameraRig](https://img-blog.csdnimg.cn/9384bdae15e64099b7befa7629efcce9.png)