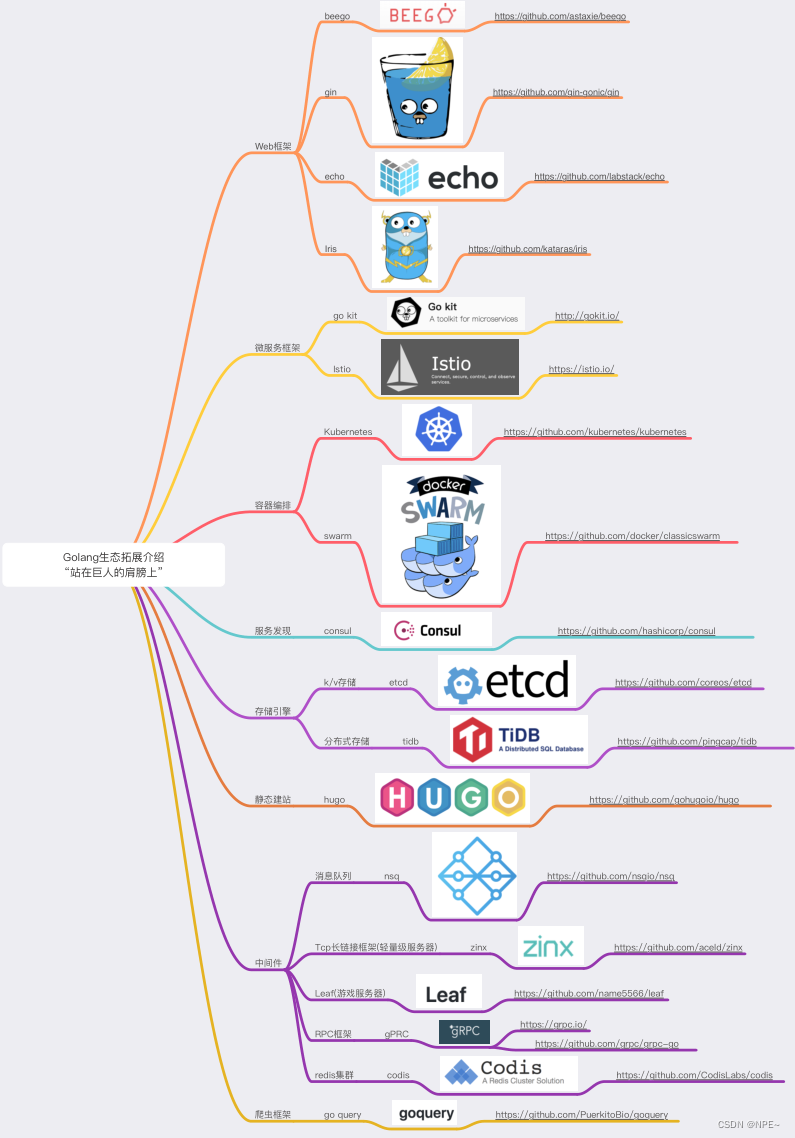
斐波那契数列问题介绍:
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=1,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)在现代物理、准晶体结构、化学等领域,斐波那契数列都有直接的应用,为此,美国数学会从 1963 年起出版了以《斐波那契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
第一、第二项都是1,从第三项开始F(n)=F(n - 1)+F(n - 2),这个使用递归很容易求解:
几行代码就能解决:
public static int fib(int n) {
if( n == 0) return 0;
if(n <= 2) return 1;
return fib(n - 1) + fib(n-2);
}对斐波那契数列的求解我们有以下的思考:
1)斐波那契数列的线性求解(O(N))的方式非常好理解
2)同时利用线性代数,也可以改写出另一种表示
| F(N) , F(N-1) | = | F(2), F(1) | * 某个二阶矩阵的N-2次方
//|f(3) f(2)| = |f(2) f(1)| * base //|f(4) f(3)| = |f(3) f(2)| * base //|f(4) f(3)| = |f(2) f(1)| * base的平方
3)求出这个二阶矩阵,进而最快求出这个二阶矩阵的N-2次方
//因为f(n)肯定是一个整数,而原来的|f(2) f(1)|是一行两列,所以base是2行(要与|f(2) f(1)|的列数相同),有因为结果是一行两列
//所以base的列数也是2,我们假设矩阵是{{a,b},{c,d}}
//|2 1| = |1 1| * base得出 1*a + 1 * c = 2 1 * b+ 1 *d = 1
//|3 2| = |2 1| * base得出 2*a+1*c=3 2*b+1*d=2,两个推出a = 1, b = 1, c =1 ,d=0
//所以求解出base矩阵是{{1,1},{1,0}}
怎么去求矩阵的n次方呢?我们先看某个数的n次方,比如10的75次方,但是10*10*10...10乘75次的话,那不还是O(N)的时间复杂度吗,这里有别的路径75=64+8+2+1, ,那怎么快速的得到1,2,8,64次方呢,10 本身是10的1次方 10*10(a)就是10的2次方,a*a(b)就是10的四次方, b*b(c)就是10的8次方,c*c(d)就是10的16次方,d*d(e)就是10的32, e*e(f)就是10的64次方,我们一共算了6次,加上10本身也就顶多7次,接近O(longN)。75对应的二进制数是 ....1001011只要把二进制中1,2,8,64所代表的1乘入当前结果就可以了
这种解法的时间复杂度就变成了O(logN)
下面上代码,依然有非常详细的注释:
package dataStructure.fibonacci;
import static dataStructure.danDiaoZhan.SumOfSubarrayMinimums.printArr;
public class FibonacciStandard {
public static int fib(int n) {
if( n == 0) return 0;
if(n <= 2) return 1;
return fib(n - 1) + fib(n-2);
}
public static int fib2(int n) {
if(n == 0) return 0;
if(n <= 2) return 1;
//大于2的时候f(n) = f(n-1) + f(n-2)是稳定的递推结构,有稳定的位置依赖,可以使用矩阵求解
//|f(3) f(2)| = |f(2) f(1)| * base
//|f(4) f(3)| = |f(3) f(2)| * base
//|f(4) f(3)| = |f(2) f(1)| * base的平方
//
//因为f(n)肯定是一个整数,而原来的|f(2) f(1)|是一行两列,所以base是2行(要与|f(2) f(1)|的列数相同),有因为结果是一行两列
//所以base的列数也是2,我们假设矩阵是{{a,b},{c,d}}
//|2 1| = |1 1| * base得出 1*a + 1 * c = 2 1 * b+ 1 *d = 1
//|3 2| = |2 1| * base得出 2*a+1*c=3 2*b+1*d=2,两个推出a = 1, b = 1, c =1 ,d=0
//所以求解出base矩阵是{{1,1},{1,0}}
int[][] base = {{1,1},{1,0}};
//|f(n) f(n - 1)| = |f(2) f(1)| * base的n-2次方
//先计算base的n-2次方
int[][] matrix = matrixPower(base, n-2);
//|f(2) f(1)|是{{1,1}}
int[][] matrix21 = {{1,1}};
//计算|f(2) f(1)|乘以base的n-2次方
matrix = product(matrix21, matrix);
//返回的结果只有一行{{f(n) f(n-1)}}
//[0][0]就是f(n)
return matrix[0][0];
}
public static int[][] matrixPower(int[][] m, int p) {
int[][] res = new int[m.length][m.length];
//先构建单位矩阵,也就是m的0次方
for(int i = 0; i < res.length; i++) {
res[i][i] = 1;
}
//矩阵的1次方,这里是为了在不改变m的情况下使用它的平方,4次方,8次方。。。64次方
int[][] t = m;
for(;p != 0; p >>= 1) {
//最右侧是不是1,用完之后右移一位相当于比较上一位
//拿个数字举例子,75=64+8+2+1,分别是从右往左第7,4,2,1位是1,也就是...1001011
//分别是t * t^2 * t^8 * t^64
//t是刚开始进循环的时候t^2是第二次进来的时候,t^8是第四次进来的时候,t^64是第7次进来的时候
//也就是我们对于75只用了7次,基本是log(N)的级别
if((p & 1) != 0) {
res = product(res, t);
}
//每次自己变自己的平方依次求2,4,8,16,32,64次方
t = product(t,t);
}
return res;
}
public static void main(String[] args) {
int result = fib(7);
System.out.println(result);
int[][] matrix1 = {{2,1}};
int[][] matrix2 = {{1,1}, {1,0}};
int[][] matrix = product(matrix1, matrix2);
if(matrix != null)
printArr(matrix);
int n = 7;
int resultn = fib2(n);
System.out.println(resultn);
}
public static int[][] product(int[][] matrix1, int[][] matrix2) {
//第一个矩阵的行要和第二个矩阵的列相等
if(matrix1 == null || matrix2 == null || matrix1[0] == null || matrix2[0] == null || matrix1[0].length != matrix2.length) {
return null;
}
//第一个矩阵的行数
int n = matrix1.length;
//第二个矩阵的列数
int m = matrix2[0].length;
//第一个矩阵的列数也是第二个矩阵的行数,用于循环里面的计算项
int k = matrix1[0].length;
int[][] matrix = new int[n][m];
for(int i = 0; i < n; i++) {
for(int j = 0; j < m; j++) {
matrix[i][j] = 0;
for(int k1 = 0; k1 < k; k1 ++) {
matrix[i][j] += matrix1[i][k1] * matrix2[k1][j];
}
}
}
return matrix;
}
}
可能想理解这个你需要复习一下大学时候线性代数的东西:矩阵的乘法
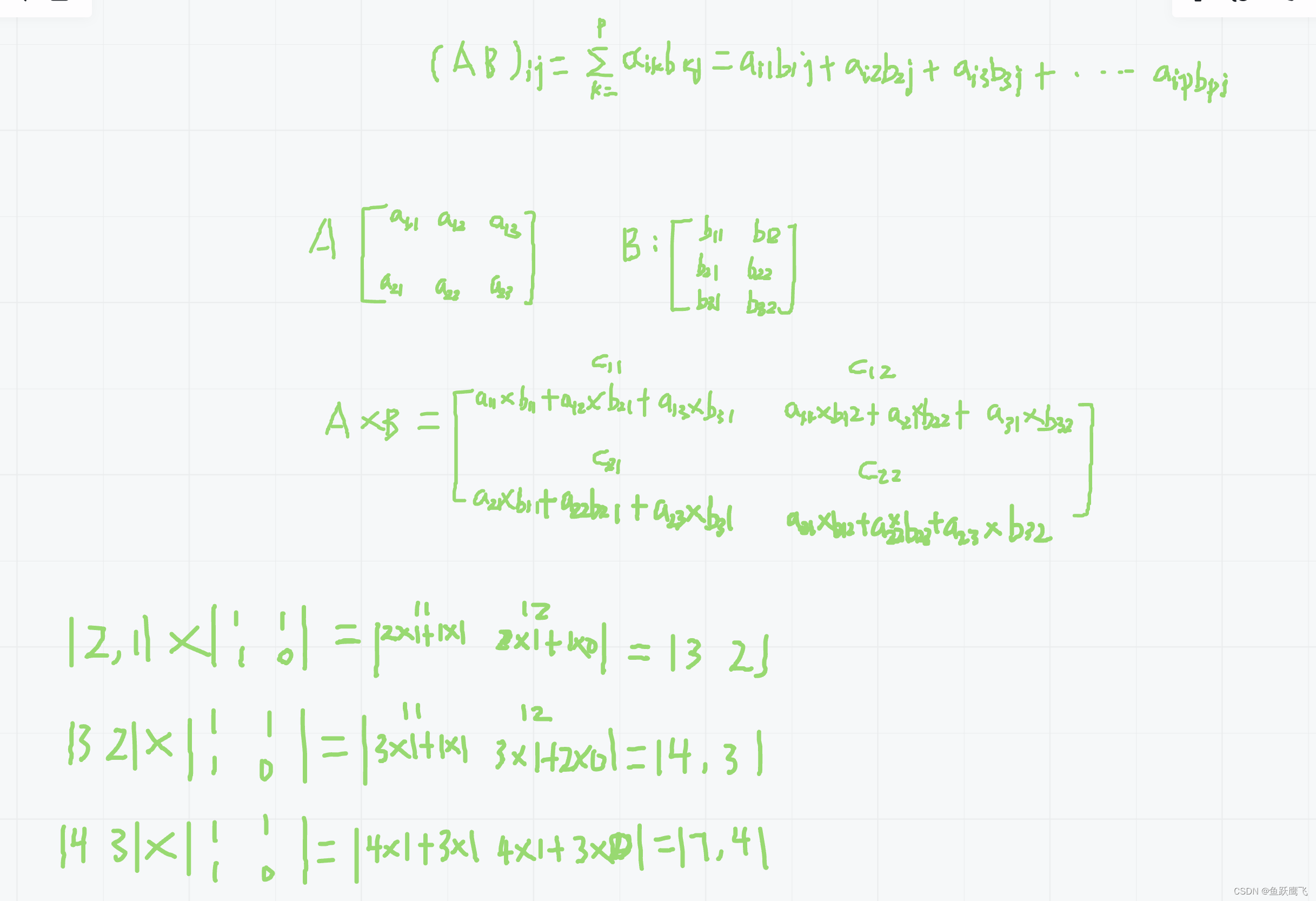
看不懂这个分析的话可以看一下百度百科里的解释
矩阵乘法_百度百科