一、不同进制之间的转换

二、逻辑代数基础

三、门电路

四、组合逻辑电路

五、半导体存储电路

六、时序电路

一、不同进制之间的转换

二-十转换：

十-二转换：

二-十六转换

十六-二转换

八-二转换

二-八转换

十六-十转换：

先转换成二进制，然后再从二进制开始转换。

二进制算数运算：

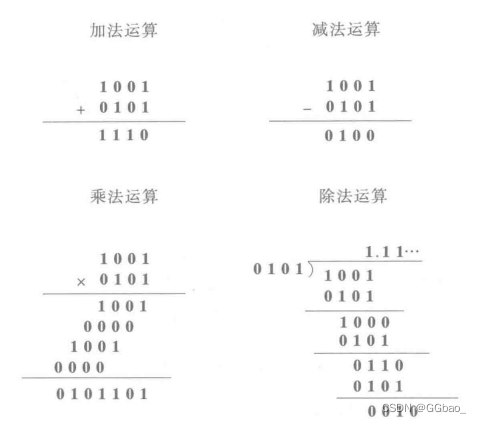
当两个二进制数表示数量大小时，他们之间可以进行数值运算，这种运算称为算数运算。特点：即二进制数的乘法运算可以通过若干次的“被乘数(或零)左移1位”和“被乘数(或零)与部分积相加”这两种操作完成;而二进制数的除法运算能通过若干次的“除数右移1位”和“从被除数或余数中减去除数”这两种操作完成。

反码、补码和补码运算：

在二进制数的前面增加一位符号位。符号位为0表示这个数是正数,符号位为1表示这个数是负数。这种形式的数称为原码。

10-5的减法运算可以用10+7的加法运算代替。因为5和7相加正好等于产生进位的模数12,所以我们称7为-5对模12的补数,也称为补码(Complement ) 。在舍弃进位的条件下，减去某个数可以用加上它的补码来替代。

二进制正数的补码就是其源码，二进制复数的补码是将其每一位取反加一。

格雷码：又称循环码，每一位的状态变化都按一定的顺序循环，相邻两个代码之间只有一位变化。

二、逻辑代数基础

所谓“逻辑”,在这里是指事物间的因果关系。当两个二进制数码表示不同的逻辑状态时,它们之间可以按照指定的某种因果关系进行推理运算。我们将这种运算称为逻辑运算。

布尔代数是指逻辑运算的数学方法，被广泛应用于解决开关电路和数字逻辑电路的分析和设计中，所以布尔代数也被称为开关代数或逻辑代数。

逻辑代数的基本运算有与（AND）、或（OR）、非（NOT）三种。用·表示与、用＋表示或、用'表示非。

Y=A·B Y=A+B Y=A'

同时,将实现与逻辑运算的单元电路称为与门,将实现或逻辑运算的单元电路称为或门,将实现非逻辑运算的单元电路称为非门(也称为反相器)。

常见复合逻辑运算有与非（NAND）、或非（NOR）、与或非（AND-NOR）、异或（EXCLUSIVE-OR）、同或（EXCLUSIVE NOR）

逻辑代数的基本公式和常用公式：也称布尔恒等式

式( 1) , ( 2) ,(11)和(12)给出了变量与常量间的运算规则。

式(3)和(13)是同一变量的运算规律,也称为重叠律。

式(4)和(14)表示变量与它的反变量之间的运算规律,也称为互补律。

式(5)和(15)为交换律,

式(6)和(16)为结合律,式(7)和( 17)为分配律。

式(8)和(18)是著名的德·摩根( De.Morgan)定理,亦称反演律。在逻辑函数的化简和变换中经常要用到这一对公式。

式(9)表明,一个变量经过两次求反运算之后还原为其本身,所以该式又称为还原律。

式(10)是对0和1求反运算的规则,它说明0和1互为求反的结果。

逻辑代数的基本定理：

带入定理：在任何一个包含变量A的逻辑等式中,若以另外一个逻辑式代人式中所有A的位置,则等式仍然成立。这就是所谓的代入定理。

反演定理：对于任意一个逻辑式Y,若将其中所有的“·"换成“+”,“+"换成“·”,0换成1,1换成0,原变量换成反变量,反变量换成原变量,则得到的结果就是Y'。这个规律称为反演定理。在使用反演定理时,还需注意遵守以下两个规则:1仍需遵守“先括号,然后乘,最后加”的运算优先次序。2不属于单个变量上的反号应保留不变。

对偶定理：若两逻辑式相等,则它们的对偶式也相等,这就是对偶定理。所谓对偶式是这样定义的:对于任何一个逻辑式Y,若将其中的“·”换成“+”，“+”换成”。”,0换成1,1换成0,则得到一个新的逻辑式Y,这个Y就称为Y的对偶式,或者说Y和Y互为对偶式。

逻辑函数及其描述方法：如果以逻辑变量作为输入,以运算结果作为输出,那么当输人变量的取值确定之后,输出的取值便随之而定。因此,输出与输入之间乃是一种函数关系。这种函数关系称为逻辑函数( logic function) ,写作Y=F(A ,B ,C,...).

逻辑函数的描述方法：逻辑真值表法、逻辑函数式、逻辑图、波形图。

逻辑方法之间的转换：

由真值表写出逻辑函数式的一般方法：

①找出真值表中使逻辑函数Y=1的那些输人变量取值的组合。

②每组输入变量取值的组合对应一个乘积项,其中取值为1的写入原变量,取值为0的写人反变量。

③将这些乘积项相加,即得Y的逻辑函数式。由逻辑式列出真值表就更简单了。这时只需将输人变量取值的所有组合状态逐一代入逻辑式求出函数值,列成表,即可得到真值表。

逻辑函数式与逻辑图的相互转换:
从给定的逻辑函数式转换为相应的逻辑图时,只要用逻辑图形符号代替逻辑函数式中的逻辑运算符号并按运算优先顺序将它们连接起来,就可以得到所求的逻辑图了。
而在从给定的逻辑图转换为对应的逻辑函数式时,只要从逻辑图的输人端到输出端逐级写出每个图形符号的输出逻辑式,就可以在输出端得到所求的逻辑函数式了。
波形图与真值表的相互转换：

在从已知的逻辑函数波形图求对应的真值表时,首先需要从波形图上找出每个时间段里输入变量与函数输出的取值,然后将这些输入﹑输出取值对应列表,就得到了所求的真值表。

在将真值表转换为波形图时,只需将真值表中所有的输入变量与对应的输出变量取值依次排列画成以时间为横轴的波形,就得到了所求的波形图,如我们前面已经做过的那样。

逻辑函数化简方法：

公式化简法：公式化简法的原理就是反复使用逻辑代数的基本公式和常用公式消去函数式中多余的乘积项和多余的因子,以求得函数式的最简形式。

①并项法：公式AB+AB'=A可以将两项合并为一项

②吸收法：公式A+AB=A可将AB项消去

③消项法：公式AB+A'C+BC=AB+A'C及AB+A'C+BCD=AB+A'C将BC或BCD项消去、

④消因子：公式A+A'B=A+B可将A'B中的A'消去

⑤配项法：公式中的A+A=A可以在逻辑函数式中重复写入某一项

卡诺图化简：是一种基于最小项的化简方法。基本化简原理就是具有相邻性的最小项可以合并,并消去不同的因子。

卡诺图化简法的步骤
用卡诺图化简逻辑函数时可按如下步骤进行:

(1)将函数化为最小项之和的形式。
(2）画出表示该逻辑函数的卡诺图。

(3）找出可以合并的最小项。
(4）选取化简后的乘积项。选取的原则是:
①这些乘积项应包含函数式中所有的最小项(应覆盖卡诺图中所有的1)。

②所用的乘积项数目最少。也就是可合并的最小项组成的矩形组数目最少。
③每个乘积项包含的因子最少。也就是每个可合并的最小项矩形组中应包含尽量多的最小项。

三、门电路

用以实现基本逻辑运算和复合逻辑运算的单元电路称为门电路(Gate Circuit )或逻辑门( Logic Gate)。门电路是数字集成电路中最基本的逻辑单元。常用的门电路在逻辑功能上有与门,或门.非门,与非门,或非门.与或非门.异或门等几种。

S断开时,输出电压vo为高电平(Vcc );而当S接通以后,输出便为低电平(等于零)。开关S是用半导体三极管组成的。只要能通过输入信号v1控制三极管工作在截止和导通两个状态,它们就可以起到图中开关S的作用。单开关电路的主要缺点是功耗比较大。

在互补开关电路中,S1和S2两个开关虽然受同一个输入信号v1控制,但它们的开关状态是相反的。当v1使S2接通的同时,使S1断开,则v0为低电平;当v1使S1接通的同时,使S2断开,则vo为高电平。因为无论v0是高电平还是低电平,S1和S2总有一个是断开的,所以流过S1和S2的电流始终为零,电路的功耗极小。因此,这种互补式的开关电路在数字集成电路中得到了广泛应用。

二极管：

TTL门电路：

四、组合逻辑电路

根据逻辑功能的不同特点，可以将数字电路分成两大类：组合逻辑电路、时序逻辑电路。在组合逻辑电路中,任意时刻的输出仅仅取决于该时刻的输入,与电路原来的状态无关。这就是组合逻辑电路在逻辑功能上的共同特点。

常用组合逻辑电路：编码器、译码器、数据选择器

加法器：

1位加法器：

半加器：如果不考虑有来自低位的进位将两个Ⅰ位二进制数相加,称为半加。实现半加运算的电路称为半加器。

AB是两个加数，S是相加的和，CO是向高位进位。

全加器：在将两个多位二进制数相加时,除了最低位以外,每一位都应该考虑来自低位的进位,即将两个对应位的加数和来自低位的进位3个数相加。这种运算称为全加,所用的电路称为全加器。

多位加法器：两个多位数相加时每一位都是带进位相加的,因而必须使用全加器。只要依次将低位全加器的进位输出端CO接到高位全加器的进位输人端CI ,就可以构成多位加法器了。

串行进位加法器：每一位的相加结果都必须等到低一位的进位产生以后才能建立起来,因此将这种结构的电路称为串行进位加法器(或称为行波进位加法器)。这种加法器的最大缺点是运算速度慢。在最不利的情况下,做一次加法运算需要经过4个全加器的传输延迟时间(从输入加数到输出状态稳定建立起来所需要的时间)才能得到稳定可靠的运算结果。但考虑到串行进位加法器的电路结构比较简单,因而在对运算速度要求不高的设备中,这种加法器仍不失为一种可取的电路。

超前进位加法器：通过逻辑电路事先得出每一位全加器的进位输入信号,而无需再从最低位开始向高位逐位传递进位信号了,这就有效地提高了运算速度。采用这种结构形式的加法器称为超前进位(CarryLook-ahead)加法器,也称为快速进位(Fast Carry)加法器。

组合逻辑电路中竞争冒险：我们将门电路两个输入信号同时向相反的逻辑电平跳变(一个从1变为0,另一个从0变为1)的现象称为竞争。应当指出,有竞争现象时不一定都会产生尖峰脉冲。由于竞争而在电路输出端可能产生尖峰脉冲的现象就称为竞争-冒险。

检查竞争冒险的方法：如果输出端门电路的两个输人信号A和A'是输入变量A经过两个不同的传输途径而来的,那么当输入变量A的状态发生突变时输出端便有可能产生尖峰脉冲。因此,只要输出端的逻辑函数在一定条件下能简化成Y=A+A'或Y=AA'，则可判定存在竞争-冒险现象。电路的输出端是或非门、与非门,同样也存在竞争-冒险现象。这时的输出应能写成Y=(A+A')'或者Y=(AA')'的形式。

消除竞争冒险的方法：

①接入滤波电容：把尖峰脉冲的幅度削弱至门电路的阈值。这种方法的优点是简单易行,而缺点是增加了输出电压波形的上升时间和下降时间,使波形变坏。

②引入选通脉冲：

③修改逻辑设计：

接滤波电容的方法简单易行,但输出电压的波形随之变坏。因此,只适用于对输出波形的前、后沿无严格要求的场合。引人选通脉冲的方法也比较简单,而且不需要增加电路元件。但使用这种方法时必须设法得到一个与输入信号同步的选通脉冲,对这个脉冲的宽度和作用的时间均有严格的要求。至于修改逻辑设计的方法,倘能运用得当,有时可以收到令人满意的效果。

五、半导体存储电路

将用于存储一组数据的存储电路叫做寄存器(Register) ,将用于存储大量数据的存储电路叫做存储器( Memory )。半导体存储电路中使用的存储单元可以分为静态存储单元和动态存储单元两大类。静态存储单元由门电路连接而成,其中包括各种电路结构形式的锁存器和触发器。只要不切断供电电源,静态存储单元的状态会一直保持下去。动态存储单元则是利用电容的电荷存储效应来存储数据的。由于电容的充放电需要一定的时间,因而它的工作速度低于静态存储单元。而且,电容上存储的电荷会随着时间的推移而逐渐泄漏,必须定期进行“刷新”(即将原来的数据重新写人) ,才能保证数据不会丢失。虽然如此,由于动态存储单元的电路结构十分简单,所以仍然被广泛用于大容量的存储器当中。寄存器由一组触发器组成,每个触发器的输入和输出都有引出端,可以直接和周围电路连接,快速地进行数据交换。由n个触发器组成的寄存器可以存储一组n位的二值数据。

SR锁存器

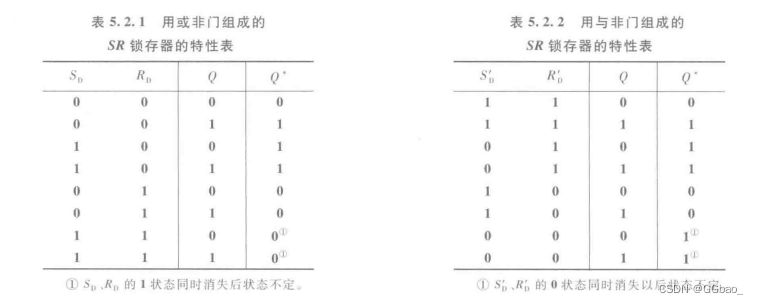
SR锁存器( Set-Reset Latch)是静态存储单元当中最基本,也是电路结构最简单的一种。通常它由两个或非门或者与非门组成。

触发器

触发器与锁存器的不同在于,它除了置1,置0输入端以外,又增加了一个触发信号输入端。只有当触发信号到来时,触发器才能按照输入的置1、置0信号置成相应的状态,并保持下去。我们将这个触发信号称为时钟信号(CLOCK) ,记作CLK。触发信号的工作方式可以分为电平触发﹑边沿触发和脉冲触发三种。

电平触发的触发器：

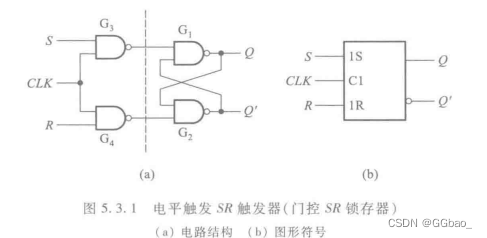
边沿触发的触发器：

脉冲触发器：

触发器按照逻辑功能分类

SR触发器

JK触发器

T触发器

D触发器

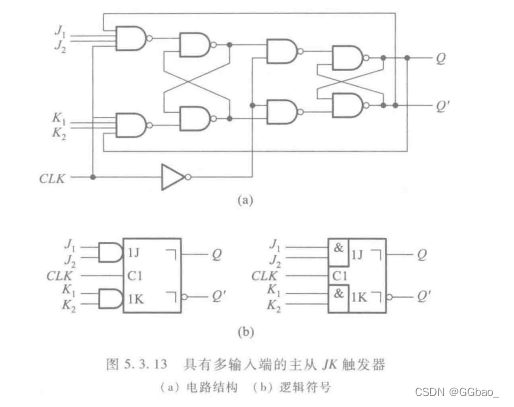
将JK 、SR ,T"三种类型触发器的特性表比较一下不难看出,其中JK触发器的逻辑功能最强，它包含了SR触发器和T触发器的所有逻辑功能。因此,在需要使用SR触发器和T触发器的场合完全可以用JK触发器来取代。例如 ,在需要SR触发器时,只要将JK触发器的JK端当作S.R端使用,就可以实现SR触发器的功能;在需要T触发器时,只要将JK连在一起当作T端使用,就可以实现T触发器的功能

触发器的动态特性

建立时间：建立时间是指输入信号应当先于时钟信号CLK动作沿到达的时间

保持时间：保持时间是指时钟信号CLK动作沿到达后,输入信号仍然需要保持不变的时间.

传输时间：传输延迟时间是指从CLK动作沿到达开始,直到触发器输出的新状态稳定建立所需要的时间

最高时钟频率：最高时钟频率是指触发器在连续、重复翻转的情况下,时钟信号可以达到的最高重复频率。CLK的低电平的持续时间必须大于建立时间。

六、时序电路

任一时刻的输出信号不仅取决于当时的输人信号,而且还取决于电路原来的状态。鉴于时序电路在工作时是在电路的有限个状态间按一定的规律转换的,所以又将时序电路称为状态机(State Machine ,简称SM),有限状态机( Finite State Machine ,简称FSM)或算法状态机( Algorithmic State Machine ,简称ASM )。