一、希尔排序
希尔排序(Shell Sort)是插入排序的改进版,由 Donald Shell 在 1959 年提出。希尔排序通过将待排序序列分成多个子序列,分别进行插入排序,最后再进行一次整体的插入排序,从而提高了排序效率。
希尔排序的基本思想是将待排序序列分成若干个子序列,对每个子序列进行插入排序,使得整个序列在插入排序的基础上更加有序。具体来说,希尔排序的实现过程如下:
-
选择一个增量序列,通常为 n/2、n/4、n/8 等,其中 n 为待排序序列的长度。
-
按照增量序列将待排序序列分成若干个子序列,对每个子序列进行插入排序。
-
逐步缩小增量序列,重复步骤 2,直到增量序列为 1。
-
对整个序列进行一次插入排序,使得序列最终有序。
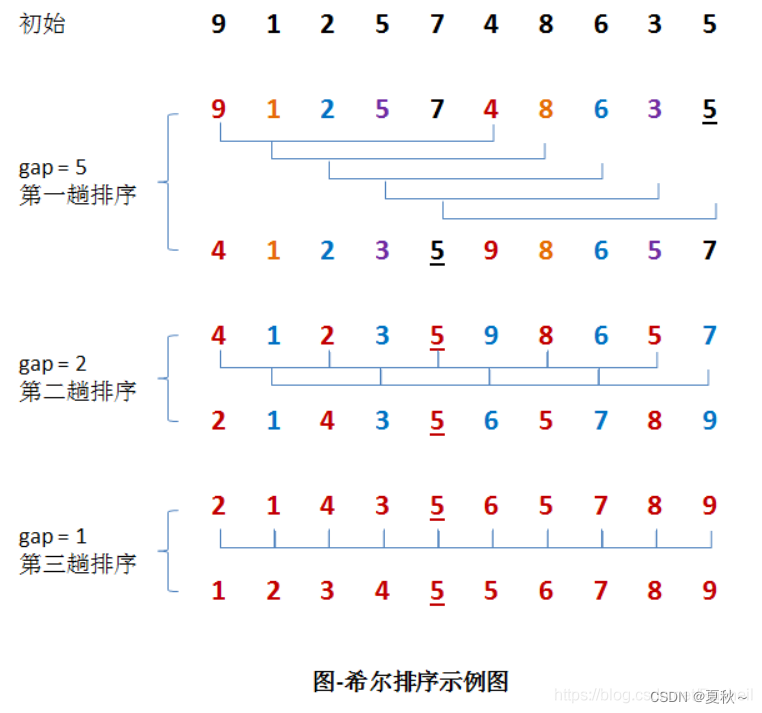
希尔排序的时间复杂度与增量序列的选择有关,通常情况下,增量序列的选择为 n/2、n/4、n/8 等,时间复杂度为 O(nlogn) ~ O(n^2)。
希尔排序的优点是相对于插入排序,它可以更快地将元素移动到正确的位置,从而减少了比较和交换的次数,提高了排序效率。缺点是其实现过程较为复杂,增量序列的选择对排序效率有较大的影响,且不同的增量序列可能导致排序结果不同。
二、希尔排序的性质
希尔排序的性质如下:
-
希尔排序是不稳定排序算法,即相等元素的相对位置可能会发生改变。
-
希尔排序的时间复杂度与增量序列的选择有关,通常情况下为 O(nlogn) ~ O(n^2)。
-
希尔排序是插入排序的改进版,通过将待排序序列分成若干个子序列,分别进行插入排序,最后再进行一次整体的插入排序,提高了排序效率。
-
希尔排序的实现过程较为复杂,增量序列的选择对排序效率有较大的影响,且不同的增量序列可能导致排序结果不同。
-
希尔排序的空间复杂度为 O(1),即排序过程中只需要常数级别的额外空间。
-
希尔排序的稳定性与增量序列的选择有关,一般情况下不稳定,但在某些特定的增量序列下可能是稳定的。
三、希尔排序的变种
希尔排序的变种有很多,其中比较常见的有以下几种:
-
Hibbard 增量序列:Hibbard 增量序列是一个经典的希尔排序增量序列,其公式为 2^k - 1,其中 k 为增量序列的索引。Hibbard 增量序列的时间复杂度为 O(n^(3/2)),性能较好。
-
Sedgewick 增量序列:Sedgewick 增量序列是另一个常用的希尔排序增量序列,其公式为 4^k + 3 * 2^(k-1) + 1 或者 4^k - 3 * 2^(k-1) + 1,其中 k 为增量序列的索引。Sedgewick 增量序列的时间复杂度为 O(n^(4/3)),性能比 Hibbard 增量序列更好。
-
希尔-奇数增量序列:希尔-奇数增量序列是一个简单的希尔排序增量序列,其公式为 2^k - 1 或者 2^(k-1) - 1,其中 k 为增量序列的索引,并且 k 为奇数。希尔-奇数增量序列的时间复杂度为 O(n^(3/2)),性能与 Hibbard 增量序列相当。
-
希尔-质数增量序列:希尔-质数增量序列是一个比较特殊的希尔排序增量序列,其公式为 2^k - 1 或者 2^(k-1) - 1,其中 k 为增量序列的索引,并且 k 是质数。希尔-质数增量序列的时间复杂度为 O(n^(3/2)),性能与 Hibbard 增量序列相当。
四、Java 实现
以下是 Java 实现希尔排序的示例代码:
public class ShellSort {
public static void sort(int[] arr) {
int n = arr.length;
// 初始化增量为 n/2,不断缩小增量直到 1
for (int gap = n / 2; gap > 0; gap /= 2) {
// 对每个子序列进行插入排序
for (int i = gap; i < n; i++) {
int temp = arr[i];
int j = i;
while (j >= gap && arr[j - gap] > temp) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp;
}
}
}
public static void main(String[] args) {
int[] arr = { 3, 5, 1, 4, 2 };
sort(arr);
System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5]
}
}
在上面的示例代码中,我们首先初始化增量为 n/2,然后不断缩小增量直到 1。对于每个增量,我们将待排序序列分成若干个子序列,对每个子序列进行插入排序。最后,对整个序列进行一次插入排序,使得序列最终有序。
五、希尔排序的应用场景
希尔排序的应用场景包括:
-
对于需要排序的数据量较大的数组或列表,希尔排序可以比插入排序更快地将数据排序。
-
希尔排序可以作为其他排序算法的预处理步骤,例如在快速排序和归并排序中,可以使用希尔排序对数据进行预处理,以提高排序效率。
-
希尔排序可以用于对链表进行排序,由于链表的特殊性质,插入排序的效率较低,而希尔排序可以通过对链表的节点进行分组来提高排序效率。
-
希尔排序是一种原地排序算法,不需要额外的空间,可以在空间有限的情况下进行排序。
=希尔排序适用于需要排序的数据量较大的情况,可以作为其他排序算法的预处理步骤,也可以用于对链表进行排序。由于希尔排序是一种原地排序算法,因此可以在空间有限的情况下进行排序。
六、希尔排序在spring 中的应用
在 Spring 框架中,希尔排序主要应用于对 BeanDefinition 的排序。
在 Spring 的 IoC 容器中,BeanDefinition 是描述 Bean 实例的元数据对象,它包含了 Bean 实例的类名、属性、构造函数等信息。在容器启动时,需要将所有的 BeanDefinition 进行排序,以保证 Bean 实例的依赖关系正确。
Spring 使用的排序算法就是希尔排序,它通过对 BeanDefinition 的名称进行排序,以保证 BeanDefinition 之间的依赖关系正确。具体来说,Spring 使用的是基于字符串长度的希尔排序算法,它可以将 BeanDefinition 按照名称的长度进行排序,从而保证依赖关系正确。
除了在 IoC 容器中对 BeanDefinition 进行排序之外,希尔排序在 Spring 中还有其他的应用场景,例如对 AOP 切面进行排序、对拦截器进行排序等。在这些场景中,希尔排序都可以通过对对象的属性进行排序,以保证它们之间的顺序正确。