目录
一,堆的概念
二,创建堆
2.1堆的结构
2.2堆的初始化
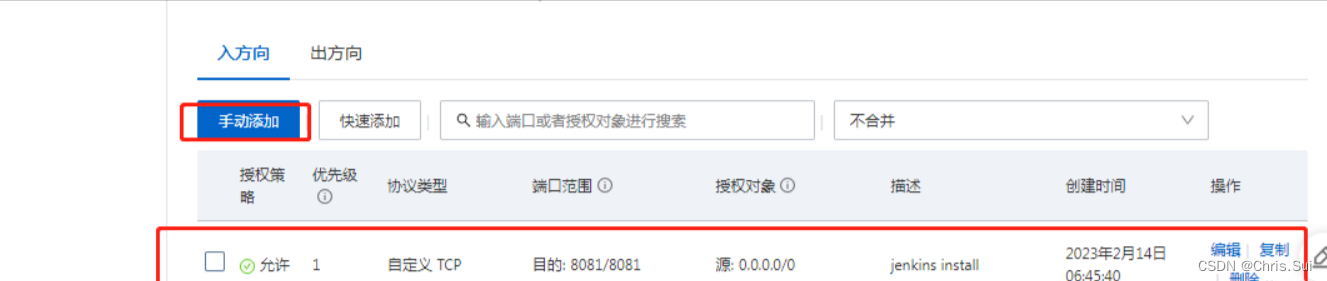
2.3堆的数据插入
2.4堆的数据的删除
注意点:
2.5 堆顶元素
2.6堆的长度
2.7堆的销毁
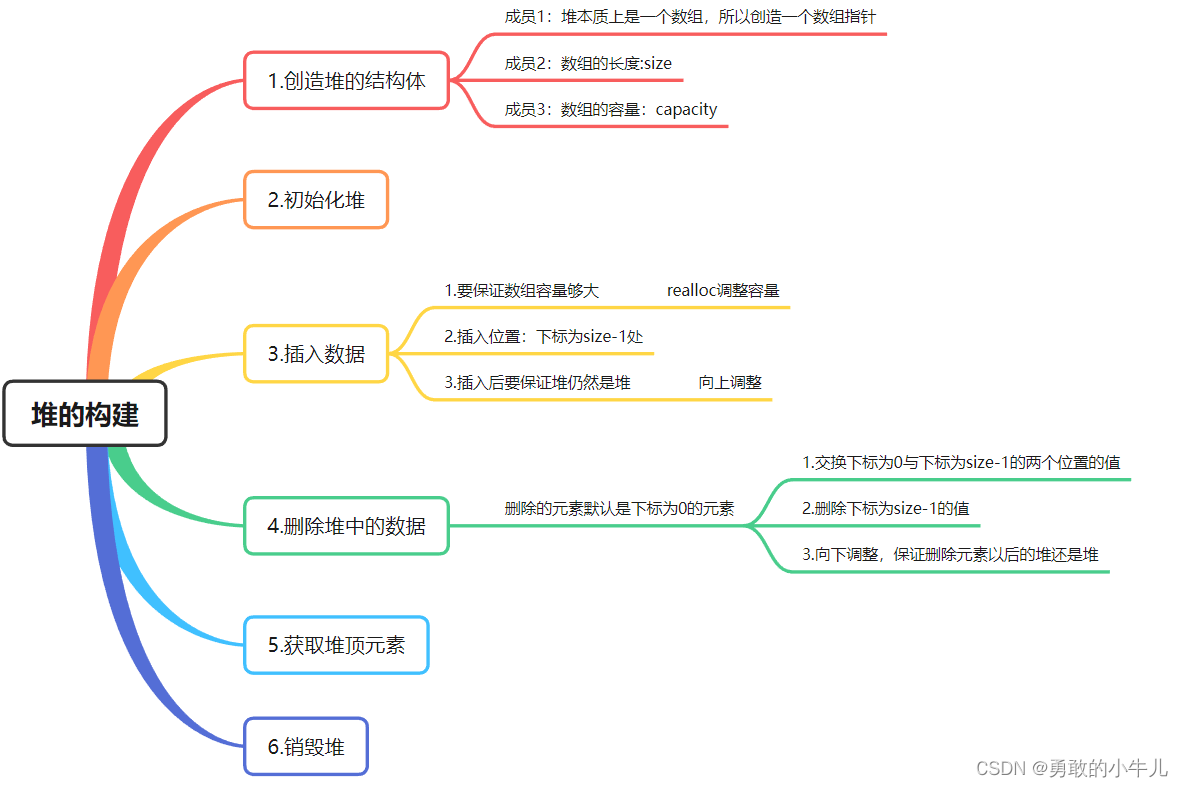
思维导图:
一,堆的概念
堆是什么?对于一个对于电脑储存结构稍有了解的人来说,堆便是一种内存空间。它是区别于栈和静态区的。但是今天我想要介绍的堆却不是这个堆,我想要介绍的这个堆在物理上就是一个数组但是在逻辑结构上就是一个满二叉树。
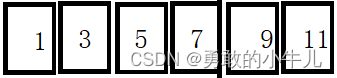
就像这样:
这个就是一个堆。这个图就是堆的一个物理结构。
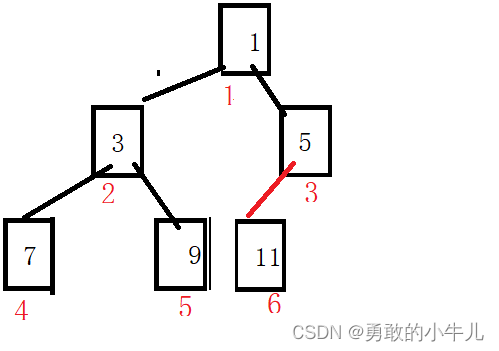
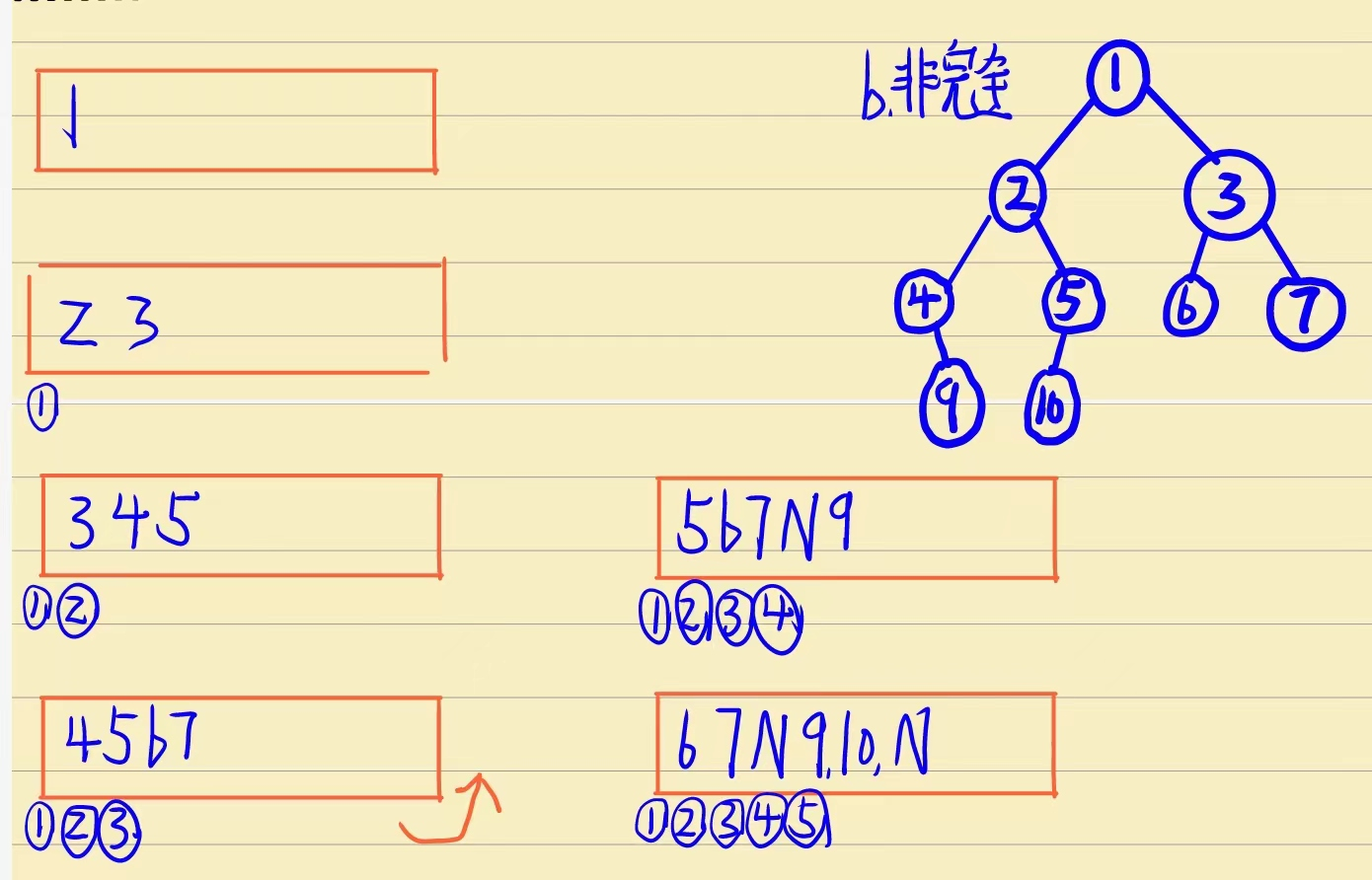
它的逻辑结构是这样的:
这个堆就是一个小堆!顺便提一句——虽然这个小堆的数组结构看起来是有序的,但是小堆不一定是有序的。我们的这个小堆只是一个特例!大堆小堆的分类的根据只是父节点与子节点之间的关系。父节点要是比子节点小那这个堆就是小堆,父节点要是比子节点要大那这个堆就是大堆!
二,创建堆
2.1堆的结构
堆,实际上就是一个数组嘛。但是你的堆可不是一个静态的数组。相反,它是一个动态的数组!所以我们的结构设计就要像顺序表一样有数组,要长度,有容量!
代码:
typedef int HeapDataType;
struct Heap {
HeapDataType* a;//堆类型的数组
int capacity;//堆的容量
int size;//堆的长度
}Heap;2.2堆的初始化
堆的初始化就是给堆内的数组,容量,长度一个初始的值!在堆内还没有数据时我们可以给堆的长度,容量都初始化为0。而数组可以初始化为NULL。
代码:
void HeapInit(Heap* php)
{
php->a = NULL;
php->capacity = 0;
php->size = 0;
}2.3堆的数据插入
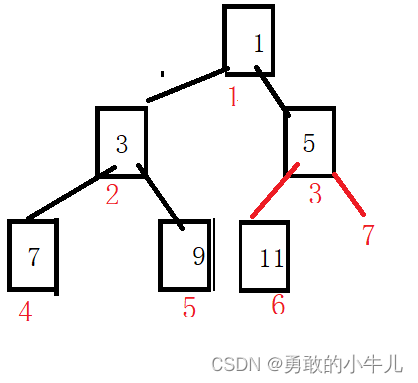
堆的数据插入这一块可能就是我们写堆这个代码的一个难点。在写这个代码的时候我们必须知道我们的这个堆的插入应该插入到哪一个位置呢?很明显就是插入到堆的在最后一个位置,在数组中就是a[size-1]这个位置。而在堆的逻辑结构中,比如这个逻辑结构:
就要插入到7这个位置。
但是,凡事都要有个前提。那就是,你插入了你想要插入的数据以后,你的堆还得是堆。 也就是说,当你是小堆的时候,你插入一个数据以后堆的父节点还得小于堆的子节点。当你是大堆的时候,你插入数据以后堆的父节点还得大于堆的子节点。那我们要如何让堆实现这个功能呢?答案就是要实现向上调整算法。在你插入数据以后不断的向上调整从而维持父节点与子节点之间的特有关系。
代码:
void AdjustUp(Heap* php, int n)
{
assert(php);
int child = n;//孩子节点的下标
int parent = (n - 1) / 2;//父亲节点的下标
while (child > 0)
{
if (php->a[child] < php->a[parent])//实现小堆——父节点与子节点的位置交换
{
int temp = php->a[child];
php->a[child] = php->a[parent];
php->a[parent] = temp;
child = parent;
parent = (child - 1) / 2;
}
else {
break;
}
}
}
void PushHeap(Heap* php,HeapDataType x)//向上调整算法
{
assert(php);//先检查php是否为NULL
if (php->size == php->capacity)//满了就扩容
{
int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;//商定新容量
php->a = (HeapDataType*)realloc(php->a,newcapacity*sizeof(HeapDataType) );
if (php->a == NULL)
{
perror("malloc fail!");
return ;
}
php->capacity = newcapacity;
}
php->size++;//堆的长度加1.
php->a[php->size - 1] = x;//在堆的最后一个位置上插入新元素
AdjustUp(php,php->size-1);//实现向上调整
}2.4堆的数据的删除
堆的数据的删除删除的是根节点还是叶子节点呢?答案是删除的是根节点。也就是堆的第一个元素。那我们要怎么删呢?我们删除的步骤一般就是将根节点与最后一个叶子节点先调换顺序,然后将最后一个叶子节点删除掉。这样就达到了删除根节点的目的。但是就和插入堆节点一样,在我们删除掉根节点以后,我们还要保证我们的堆仍然是一个堆!怎么办呢?这时候就要引入向下调整这个概念了。
什么是向下调整呢?写个代码就知道了!
代码:
bool HeapEmpty(Heap* php)
{
assert(php);
return php->size == 0;//当堆的长度为0时这个堆就是一个空堆,就返回true。
}
void swap(HeapDataType* p1, HeapDataType* p2)//交换节点函数
{
HeapDataType temp = *p1;
*p1 = *p2;
*p2 = temp;
}
void AdjustDown(Heap* php, int n)//向下调整算法
{
assert(php);//断言,防止php为NULL
int parent = 0;//最初的根节点的坐标
int child = 2 * parent + 1;//左子节点与根节点的下标关系
while (child <n )//当你要实现向下调整的时候,循环的终止条件是子节点在范围之内
{
if (child + 1 < n && php->a[child + 1] < php->a[child])//当左节点不是最小的节点时那就变成右节点来比较
{
child++;
}
if ( php->a[child] < php->a[parent])
{
swap(&php->a[parent], &php->a[child]);//交换函数
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void PopHeap(Heap* php)
{
assert(php);//断言一下php是否为NULL
assert(!HeapEmpty(php));//断言,防止堆为空
swap(&php->a[0], &php->a[php->size - 1]);//交换根节点与最后一个叶子节点
php->size--;//删除掉最后一个叶子节点,也就是将根节点删除掉了
AdjustDown(php,php->size);//向下调整来保证堆仍然是堆
}删除的步骤:
1.利用assert断言,判断php是否为NULL指针,利用HeapEmpty函数判断堆是否是空堆。
2.交换根节点与最后一个叶子节点,利用size从视觉上删除掉根节点(实际上没有删除,只是你访问不到了)
3.从根节点处向下调整,确保删除以后的堆还是一个堆。
注意点:
1.交换左右子节点时要保证右节点是存在的
2。向下调整的循环的条件是子节点的下标在数组的范围之内。
3.在执行删除操作的时候要确保堆内是有数据的。
2.5 堆顶元素
在堆中,堆顶元素就是下标为0的元素。所以找堆顶元素就是返回下标为0的元素。
代码:
HeapDataType HeapTop(Heap* php)
{
assert(php);
return php->a[0];
}2.6堆的长度
int Heapsize(Heap*php)
{
assert(php);
return php->size;//返回堆的长度
}2.7堆的销毁
void HeapDstroy(Heap* php)
{
free(php->a);//因为php->a是realloc出来的,所以为了避免内除泄漏,需要手动释放
php->a = NULL;
php->size = 0;
php->capacity = 0;
}补充:
其实,当你用这样一个代码:
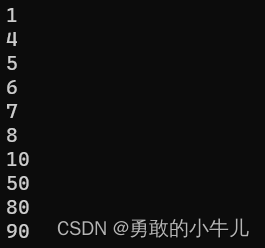
int main() { Heap hp; HeapInit(&hp); int a[10] = { 1,80,50,90,4,8,7,5,6,10 }; for (int i = 0;i < sizeof(a) / sizeof(a[0]);i++) { PushHeap(&hp, a[i]); } while (!HeapEmpty(&hp)) { printf("%d\n", HeapTop(&hp)); PopHeap(&hp); } HeapDstroy(&hp); return 0; }来打印这个堆里的元素的时候,你会发现:
这个打印结果是很有序的,但是这不是排序。这只是将堆顶元素依次打印出来的结果。