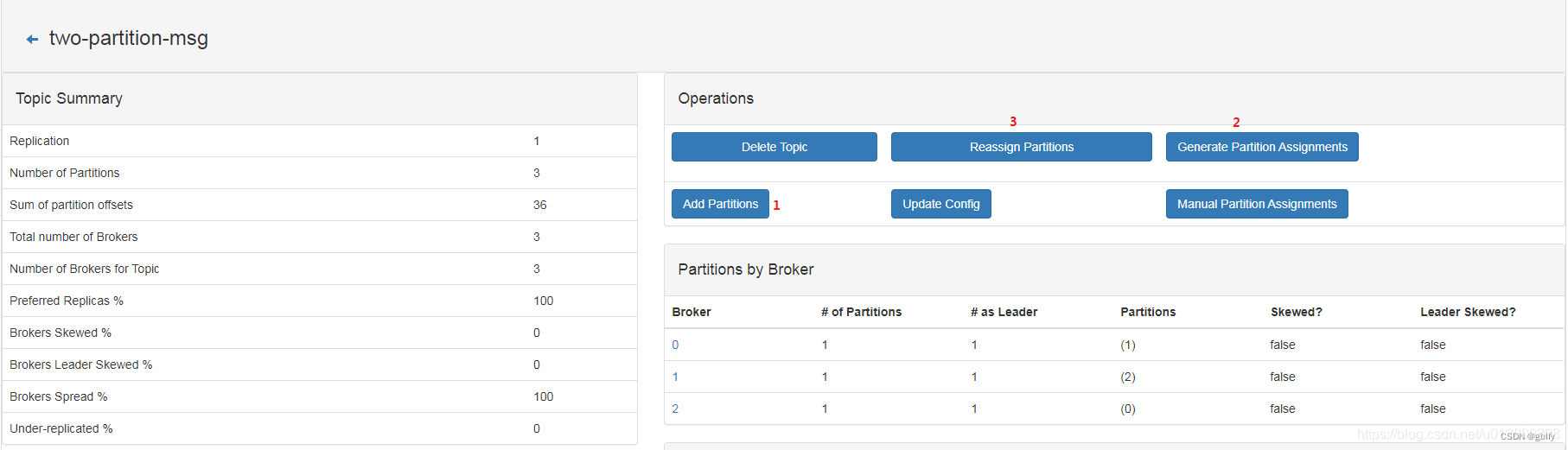
暴力循环

直观模拟，对于某个固定的盒子，可以遍历所有盒子，$\sum$ 遍历的盒子里的球数 $\times$ 遍历的盒子到固定的盒子的距离，得移动所有球到固定盒子的最小操作数。依次固定所有盒子，遍历，得到答案。

class Solution {
public:
    vector<int> minOperations(string boxes) {
        vector<int> ans(boxes.size(),0);
        for(int i = 0;i<boxes.size();i++)
            for(int j = 0;j<boxes.size();j++)
                ans[i] += (boxes[j]-'0')*abs(j-i);
        return ans;
    }
};

1. 时间复杂度 : $O(n^2)$ ， 二重遍历的时间复杂度 $O(n)$ 。
2. 空间复杂度 : $O(1)$ ， 除答案外，只使用常量级空间 。

前缀和

注意到，从当前盒子到下一盒子，相当于下一盒子左侧所有距离 $+1$ ，右侧所有距离 $-1$ 。
开个前缀和数组，保存每个位置左侧的球数(不含当前盒子)，那么每个位置右侧的最小球数(含当前盒子)可以用前缀和做差的方式求出。

提示 : 前缀和需要开 $n+1$ 个位置，$0$ 位置左侧没有盒子，前缀和的 $0$ 位置存 $0$ ，相应的，第 $n$ 个位置保存 $0$ ~ $n-1$ 所有盒子的球数。

class Solution {
public:
    vector<int> minOperations(string boxes) {
        int n = boxes.size();
        vector<int> ans(n,0);
        int pre[n+1];
        memset(pre,0,sizeof pre);
        for(int i = 1;i<=n;i++) pre[i] += pre[i-1] + boxes[i-1]-'0';
        for(int i = 1;i<n;i++) ans[0] += (boxes[i]- '0') * i;
        for(int i = 1;i<n;i++) ans[i] = ans[i-1] +pre[i] -(pre[n]-pre[i]);
        return ans;
    }
};

1. 时间复杂度 : $O(n)$ ， 三次遍历的时间复杂度 $O(n)$ 。
2. 空间复杂度 : $O(n)$ ， 前缀和数组的空间复杂度 $O(n)$ 。

滚动前缀和

一次遍历，维护后缀和变量，算出移动所有球到 $0$ 号盒子的最小操作数。再次遍历，维护前缀和，维护后缀和，利用前一个答案、前缀和、后缀和维护所有答案

class Solution {
public:
    vector<int> minOperations(string boxes) {
        int n = boxes.size();
        int post = 0;
        vector<int> ans(n,0);
        for(int i = 1;i<n;i++){
            post += boxes[i] - '0';
            ans[0] += (boxes[i]-'0')*i;
        }
        int pre = boxes[0] - '0';
        for(int i = 1;i<n;i++){
            ans[i] = ans[i-1] + pre - post;
            pre += boxes[i] - '0';
            post -= boxes[i] - '0';
        }
        return ans;
    }
};

1. 时间复杂度 : $O(n)$ ， 二次遍历的时间复杂度 $O(n)$ 。
2. 空间复杂度 : $O(1)$ ， 只使用常量级空间 。

AC