前置知识
哈佛曼树：我们先来复习一下啥叫做哈佛曼树
1.背景
我们有下面这样一个字符串需要编码，就是将下面的字符转为二进制。我们采用的方法是前缀编码，用一颗树的叶节点来放字符。
2.前缀编码
编码是咋样的呢？看下面这个例子
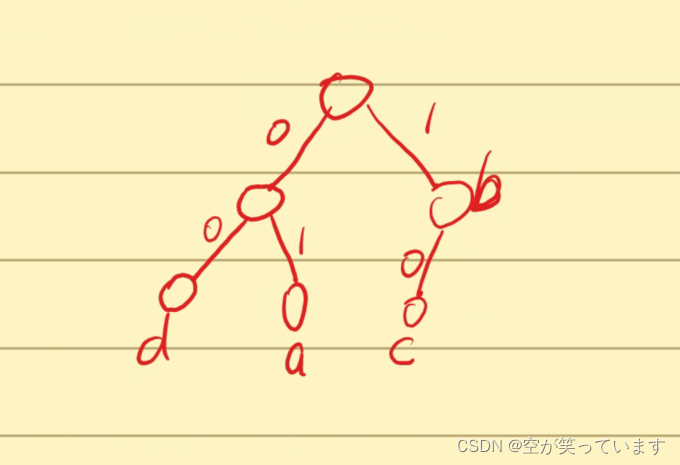
按照上面这个图片的话，那么d为00，a为01，然后b就为1，c为10.我们根据这个来编码那么编出来就为 0101111111010100000000000000000，此时就会出现一问题，如果我们将这个二进制解码的话，还能回去吗？我们来试试
看上图，显然回不去了，那么就说明上述编码不可以，所以我们需要前缀编码， 让我们来看看前缀编码是如何的。
定义可能不是很明白，来看例子
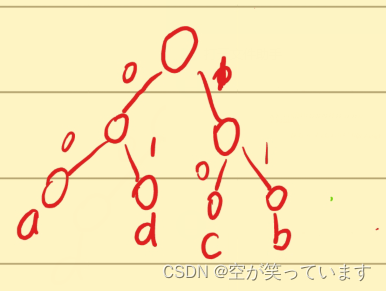
看看和刚才的有啥区别，其实就是将b下放了一层，有区别嘛？有，我们发现我们的字母都是在叶子结点，也就是说在每个存放字母的节点它到根节点之间的路径是没有其他字母节点的，那么当我们解码的时候，我们就只会唯一解码，不会出现上面出现歧义的情况。不信？我们来试试
你可以自己动手画画，你会发现当你从左往右解码的时候只有一种情况不会出现上面那种不知道如何解码的情况。
3. 哈佛曼树
哈佛曼树其实就是依据上面的写的东西来建的树。然后我们有一个目的就是让我们建的树的带权路径（WAL）是最小的 WPL=（W1L1+W2L2+W3L3+…+WnLn），就是说每个节点的中的权重然后乘以其路径之长(Wn为节点权重，Ln为路径长度)之和最小。如何使它最小呢？其过程是这样的
这样就构造了一颗WAL最小的哈佛曼树。有人可能会问为啥？我们可以来证明一下。
4.哈佛曼树最优证明
1.哈佛曼树为了满足前缀编码那就是必须存字符的节点就必须是叶节点。
2.并且总存在一个最优解（WAL最小），里面最小的两个节点是兄弟节点
这第二步我们来证明一下，我们分为两种情况。
1.两个最小是兄弟节点 。2.两个最小的不是兄弟节点。
分两种情况
两个最小的节点都在一层，那么是否是兄弟节点都无所谓。
两个最小的节点不在同一层。
题目
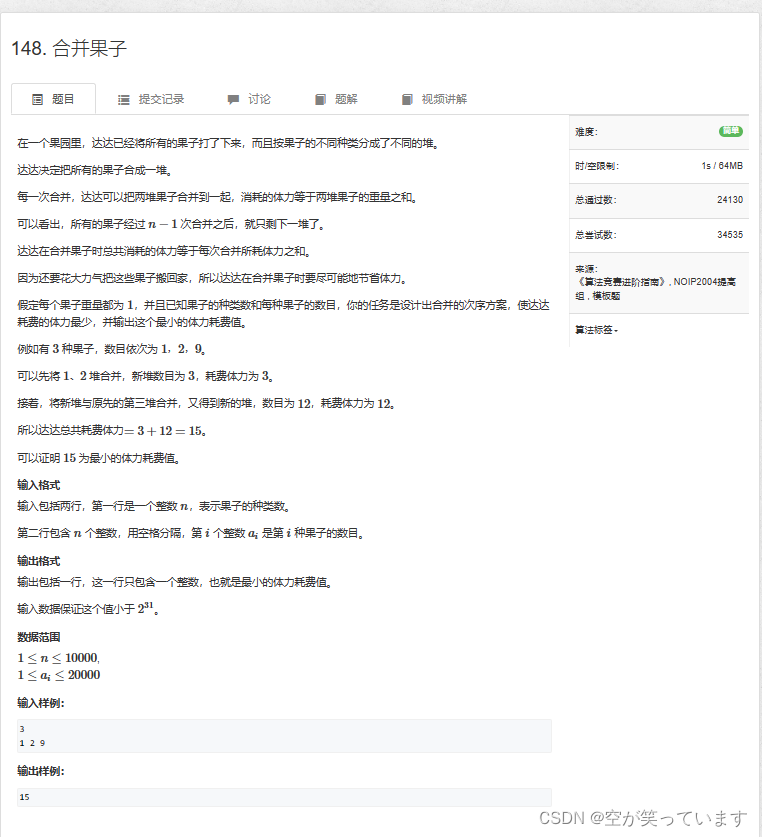
这道题按照上面的算法也就是，每次将最小的两个数拿出来，然后相加就行。
返回最小，然后删除最小的，用最小堆再适合不过了。所有就有以下代码。
#include <iostream>
#include <queue>
using namespace std;
int n;
priority_queue<int, vector<int>, greater<int> > q;
int main(){
int n;
cin>>n;
while(n--){
int a;
cin>>a;
q.push(a);
}
int res = 0;
while(q.size() > 1){
auto a = q.top();
q.pop();
auto b = q.top();
q.pop();
res += a + b;
int c = a + b;
q.push(c);
}
cout<<res;
return 0;
}
