英文源地址
本章将使用Go语言实现一个不可变地B+树.这是一个最小实现, 因此很容易理解.

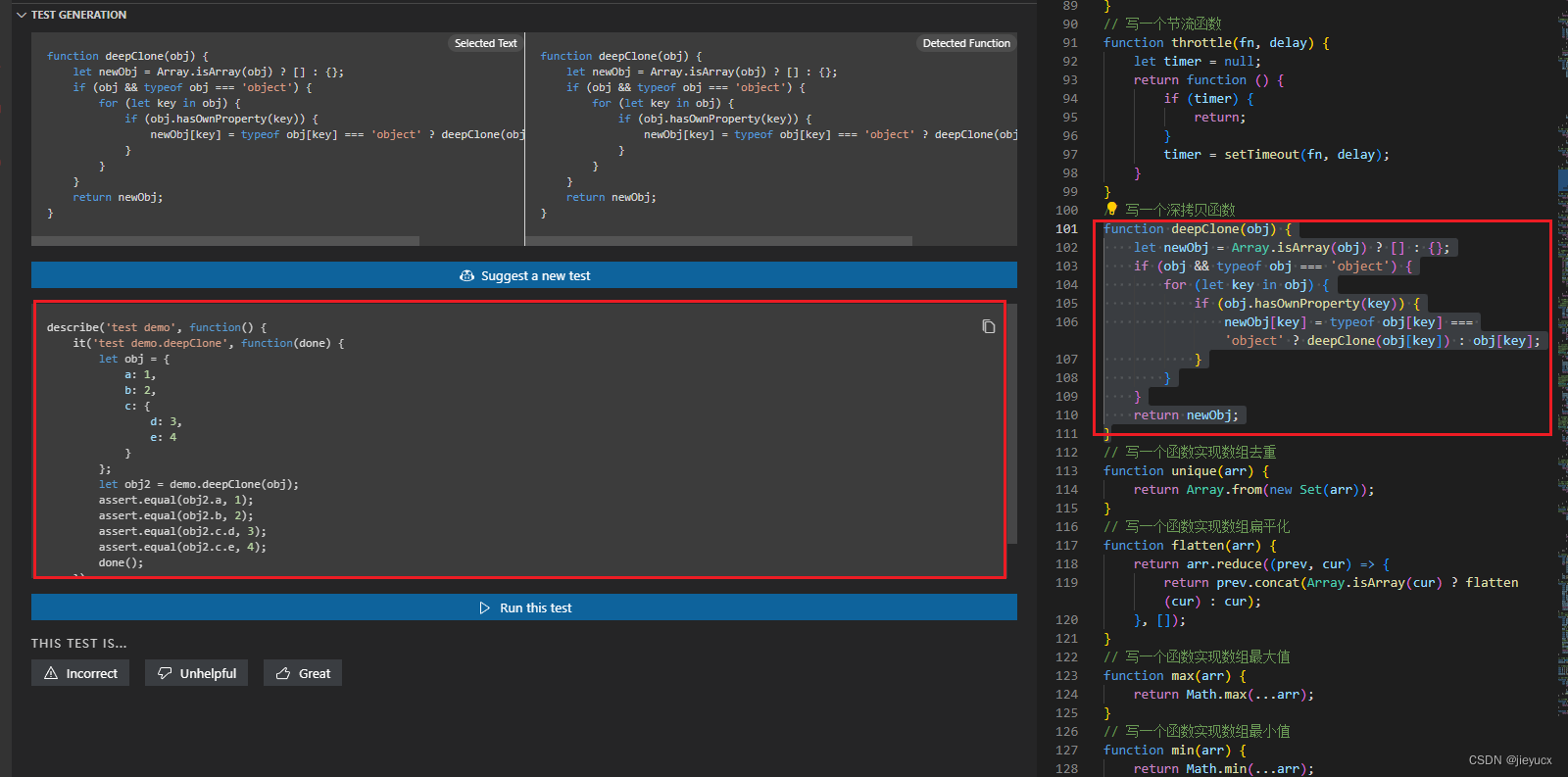
Node节点的格式

我们的B树最终将被持久化到磁盘上, 因此我们首先需要为b树节点设计数据格式.如果没有这种格式, 我们将无法知道节点的大小以及何时拆分节点.
一个节点包含:

• 一个固定大小的头部, 包含节点的类型(叶子节点或内部节点)和键的数量
• 指向子节点的指针列表(内部节点使用)
• 指向每个键值对的偏移量列表
• 封装的KV对
  
  以下是KV键值对的格式.长度后紧跟着数据.
  
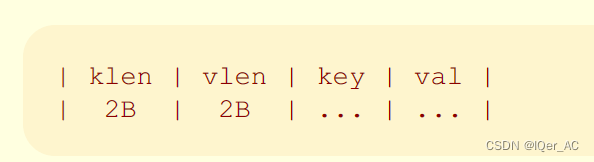
  为了简单起见, 叶子节点和内部节点都使用相同的格式.

数据类型

既然我们最终要将b树转存至磁盘, 为什么不使用字节数组作为我们的内存数据结构呢?

type BNode struct {
	data []byte
}

const (
	BNODE_NODE = 1
	BNODE_LEAF = 2
)

我们不能使用内存指针, 这些指针是64位整数, 引用磁盘页而不是内存节点.我们将添加一些回调函数来抽象这个方面, 以便我们的数据结构仍然是纯粹的数据结构代码.

type BTree struct {
	root uint64

	get func(uint64) BNode
	new func(BNode) uint64
	del func(uint64)
}

页大小定义为4K字节.更大的页面大小(如8K或16K)也可以.
我们还对键和值的大小做了一些约束.所以只有一个kv键值对的节点总是可以放在一个页上.如果需要支持更大的键或更大的值, 就必须为它们分配额外的页, 这会增加复杂度.

const HEADER = 4

const BTREE_PAGE_SIZE = 4096
const BTREE_MAX_KEY_SIZE = 1000
const BTREE_MAX_VAL_SIZE = 3000

func init() {
	node1max := HEADER + 8 + 2 + 4 + BTREE_MAX_KEY_SIZE + BTREE_MAX_VAL_SIZE
	assert(node1max <= BTREE_PAGE_SIZE)
}

解码b树节点

由于节点只是一个字节数组, 因此我们将添加一些辅助函数来访问其内容.

func (node BNode) btype() uint16 {
	return binary.LittleEndian.Uint16(node.data)
}

func (node BNode) nkeys() uint16 {
	return binary.LittleEndian.Uint16(node.data[2:4])
}

func (node BNode) setHeader(btype uint16, nkeys uint16) {
	binary.LittleEndian.PutUint16(node.data[0:2], btype)
	binary.LittleEndian.PutUint16(node.data[2:4], nkeys)
}

func (node BNode) getPtr(idx uint16) uint64 {
	assert(idx < node.nkeys())
	pos := HEADER + 8 * idx
	return binary.LittleEndian.Uint64(node.data[pos:])
}

func (node BNode) setPtr(idx uint16, val uint64) {
	assert(idx < node.nkeys())
	pos := HEADER + 8 * idx
	binary.LittleEndian.PutUint64(node.data[pos:], val)
}

关于偏移列表的一些细节

• 偏移量与第一个kv对的位置有关
• 第一个kv对的偏移量始终为零, 因此它不存储在列表里
• 我们将到最后一个kv对的偏移量存储在偏移列表, 这用于确定节点的大小

func offsetPos(node BNode, idx uint16) uint16 {
	assert(1 <= idx && idx <= node.nkeys())
	return HEADER + 8 * node.nkeys() + 2 * (idx - 1)
}

func (node BNode) getOffset(idx uint16) uint16 {
	if idx == 0 {
		return 0
	}
	return binary.LittleEndian.Uint16(node.data[offsetPos(node, idx):])
}

func (node BNode) setOffset(idx uint16, offset uint16) {
	binary.LittleEndian.PutUint16(node.data[offsetPos(node, idx):], offset)
}

偏移列表用于快速定位第n个KV键值对

func (node BNode) kvPos(idx uint16) uint16 {
	assert(idx <= node.nkeys())
	return HEADER + 8 * node.nkeys() + 2 * node.nkeys() + node.getOffset(idx)
}

func (node BNode) getKey(idx uint16) []byte {
	assert(idx < node.keys())
	pos := node.kvPos(idx)
	klen := binary.LittleEndian.Uint16(node.data[pos:])
	return node.data[pos+4:][:klen]
}

func (node BNode) getVal(idx uint16) []byte {
	assert(idx < node.nkeys())
	pos := node.kvPos(idx)
	klen := binary.LittleEndian.Uint16(node.data[pos+0:])
	vlen := binary.LittleEndian.Uint16(node.data[pos+2:])
	return node.data[pos+4+klen:][:vlen]
}

并确定节点的大小

func (node BNode) nbytes() uint16 {
	return node.kvPos(node.nkeys())
}

b树插入操作

代码被分解成了小步骤.

查找key

要将键插入叶节点, 我们需要查找它在kv列表中的位置

func nodeLookupLE(node BNode, key []byte) uint16 {
	nkeys := node.nkeys()
	found := uint16(0)
	for i := uint16(1); i < nkeys; i++ {
		cmp := bytes.Compare(node.getKey(i), key)
		if cmp <= 0 {
			found = i
		}
		if cmp >= 0	{
			break
		}	
	}
	return found
}

查找对叶子节点和内部节点都有效, 注意, 第一个键将被跳过以进行比较, 因为它已经从父节点进行了比较.

更新叶子节点

在查找到要插入的位置后, 我们要创建一个包含新键的节点副本.

func leafInsert(new BNode, old BNode, idx uint16, key []byte, val []byte) {
	new.setHeader(BNODE_LEAF, old.nkeys()+1)
	nodeAppendRange(new, old, 0, 0, idx)
	nodeAppendKV(new, idx, 0, key, val)
	nodeAppendRange(new, old, idx+1, idx, old.nkeys()-idx)
}

nodeAppendRange函数从旧节点拷贝键至新节点

func nodeAppendRange(new BNode, old BNode, dstNew uint16, srcOld uint16, n uint16) {
	assert(srcOld+n <= old.nkeys())
	assert(dstNew+n <= new.nkeys())
	if n == 0 {
		return
	}
	for i := uint16(0); i < n; i++ {
		new.setPtr(dstNew+i, old.getPtr(srcOld+i))
	}
	dstBegin := new.getOffset(dstNew)
	srcBegin := old.getOffset(srcOld)
	for i := uint16(1); i < n; i++ {
		offset := dstBegin + old.getOffset(srcOld+i) - srcBegin
		new.setOffset(dstNew+i, offset)
	}
	begin := new.kvPos(srcOld)
	end := new.kvPos(srcOld+n)
	copy(new.data[new.kvPos(dstNew):], old.data[begin:end])
}

nodeAppendKV函数复制一个kv对到新节点中

func nodeAppendKV(new BNode, idx uint16, ptr uint64, key []byte, val []byte) {
	new.setPtr(idx, ptr)
	pos := new.kvPos(idx)
	binary.LittleEndian.PutUint16(new.data[pos+0:], uint16(len(key)))
	binary.LittleEndian.PutUint16(new.data[pos+2:], uint16(len(val)))
	copy(new.data[pos+4:], key)
	copy(new.data[pos+4+uint16(len(key)):], val)
	new.setOffset(idx+1, new.getOffset(idx)+4+uint16(len(key)+len(val)))
}

递归插入

插入key的主要功能

func treeInsert(tree *BTree, node BNode, key []byte. val []byte) BNode {
	new := BNode(data: make([]byte, 2 * BTREE_PAGE_SIZE))
	idx := nodeLookupLE(node, key)
	switch node.btype() {
	case: BNODE_LEAF:
		if bytes.Equal(key, node.getKey(idx)) {
			leafUpdate(new, node, idx, key, val)
		} else {
			leafInsert(tree, new, node, idx, key, val)
		}
	case BNODE_NODE:
		nodeInsert(tree, new, node, idx, key, val)
	default:
		panic("bad node!")
	}
	return new
}

leafUpdate函数与leafInsert函数类似

处理内部节点

现在来处理内部节点.

func nodeInsert(tree *BTree, new BNode, node BNode, idx uint16, key []byte, val []byte) {
	kptr := node.getPtr(idx)
	knode := tree.get(kptr)
	tree.del(kptr)
	knode = treeInsert(tree, knode, key, val)
	nsplit, splited := nodeSplit3(knode)
	nodeReplaceKidN(tree, new, node, idx, splited[:nsplit]...)
}

分裂大节点

在节点中插入键会使其增加大小, 导致其超过页大小. 在这种情况下, 节点被分割成多个更小的节点.
允许的最大键大小和值的大小只能保证单个kv键值对始终适合于一个页.在最坏的情况下, 胖节点会分裂成3个节点(中间有一个大的kv键值对)

func nodeSplit2(left BNode, right BNode, old BNode) {
	
}

func nodeSplit3(old BNode) (uint16, [3]BNode) {
	if old.nbytes() <= BTREE_PAGE_SIZE {
		old.data = old.data[:BTREE_PAGE_SIZE]
		return 1, [3]BNode{old}
	}
	left := BNode{make([] byte, 2 * BTREE_PAGE_SIZE)}
	right := BNode{make([]byte, BTREE_PAGE_SIZE)}
	nodeSplit2(left, right, old)
	if left.nbytes() <= BTREE_PAGE_SIZE {
		left.data = left.data[:BTREE_PAGE_SIZE]
		return 2, [3]BNode{left, right}
	}
	leftleft := BNode{make([]byte, BTREE_PAGE_SIZE)}
	middle := BNode{make([]byte, BTREE_PAGE_SIZE)}
	nodesplit2(leftleft, middle, left)
	assert(leftleft.nbytes() <= BTREE_PAGE_SIZE)
	return 3, [3]BNode{leftleft, middle, right}
}

更新内部节点

在节点中插入一个键可以产生1,2或3个节点. 父节点必须相应地更新自身. 更新内部节点的代码类似于更新叶子节点的代码.

func nodeReplaceKidN(tree *BTree, new BNode, old BNode, idx uint16, kids ...BNode) {
	inc := uint16(len(kids))
	new.setHeader(BNODE_NODE, old.nkeys()+inc-1)
	nodeAppendRange(new, old, 0, 0, idx)
	for i, node := range kids {
		nodeAppendKV(new, idx+uint16(i), tree.new(node), node.getKey(0), nil)
		nodeAppendRange(new, old, idx+inc, idx+1, old.nkeys()-(idx+1))
	}
	nodeAppendRange(new, ol, idx+inc, idx+1, old.nkeys()-(idx+1))
}

我们已经完成了B树的插入操作. 删除操作和剩下代码将在下一篇进行介绍.