一、完备事件组
设E是随机试验,Ω是相应的样本空间,A1,A2,...An为Ω的一个事件组,若
(1)AiAj=
(i
j)
(2)A1A2
...
An=Ω
则称A1A2...An为样本空间的一个完备事件组,完备事件组完成了对样本空间的一个分割(意义)
二、条件概率
设A,B是两个事件,且P(B)>0,则在事件B发生的条件下,事件A发生的条件概率:
P(A|B)=P(AB)/P(B)
特例:事件A和事件B互斥,则条件概率为0.
三、全概率公式
全概率公式以加法公式和乘法公式为基础。
全概率公式:通过已知每种"原因"发生的概率,求"结果"发生的概率,"原因"发生的概率称为"先验概率",即"已知原因,分析结果"。
P(A) = P(A|B1)P(B1) + P(A|B2)P(B2) + … + P(A|Bn)P(Bn)
间接求概率P(A)。
四、贝叶斯公式
从已知"结果"发生的条件下分析各个"原因"引起的条件概率,这个条件概率称为"后验概率",即"已知结果,分析原因"。
P(Bi|A) = P(A|Bi)P(Bi) / P(A)
五、先验&后验&似然估计
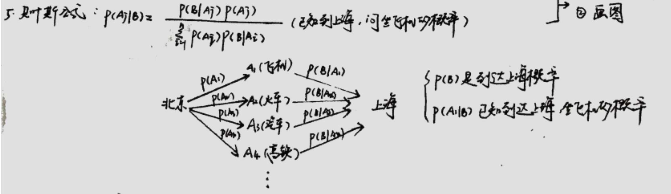
先知道"到达上海"的结果,然后由结果估计“乘坐的交通工具”的原因的概率分布,p(Ai|B),就是后验概率。
先于"到达上海"的结果,确定“乘坐的交通工具”的原因的概率分布,p(Ai),就是先验概率。
先确定原因,根据“乘坐的交通工具”的原因来估计"到达上海"的结果的概率分布,p(B|Ai),就是似然估计。
不管是什么交通方式,得到了"到达上海"的概率分布。这种不考虑原因,只看结果的概率分布,p(时间),也有一个名词:evidence(不清楚合适的中文名是什么)。
参考链接
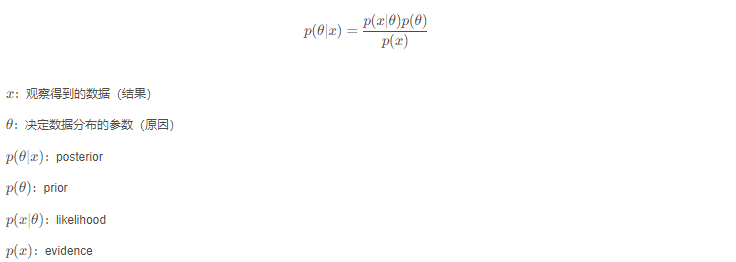






![封装window10-21H1踩的坑,无法分析或处理pass[specialize]应答文件](https://img-blog.csdnimg.cn/img_convert/fdb00eb32b5bab426ec385c6668f8b27.jpeg)

![[附源码]计算机毕业设计JAVA新冠疫苗线上预约系统](https://img-blog.csdnimg.cn/542f21ebb5e844f28223a267615c15bd.png)