递归

递归没什么好说的，直接无脑递归即可，时间复杂度：O（n），空间复杂度：O（n）

class Solution {
public:
    void midtravel(TreeNode* root,vector<int>& res)
    {
    	//当节点不为空的时候，递归下去，直到节点为空，则返回上一层，紧接处理节点
        if (root!=nullptr)
        {
            midtravel(root->left,res);
            res.push_back(root->val);
            midtravel(root->right,res);
        }
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        midtravel(root,res);
        return res;
    }
};

迭代

迭代与递归的本质其实是一致的：利用栈来维护每一个节点，只不过递归是隐式的维护了一个栈，而迭代需要你显式的维护一个栈。

图解：

pstack：栈，维护每层的节点
res：vector< int > 存储返回结果

利用一个栈维护每个节点，当节点的left不为空，则一直入栈，直到到达了叶子节点。则把栈顶元素弹出，加入到res中，同时弹出pop栈顶元素，接着遍历它的右子树。
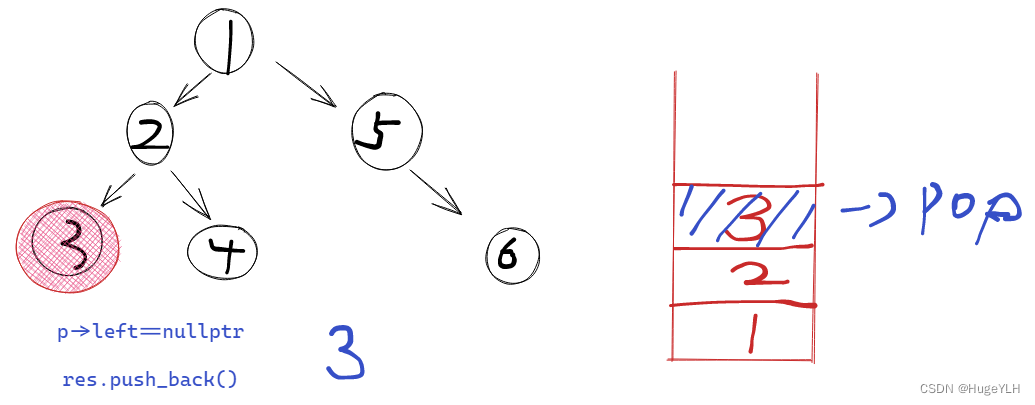
节点3的右子树为空，下一步接着弹出栈顶元素，弹出节点2，然后加入到res中，接着遍历弹出的这个节点的右子树，即为4，4节点不为空，所以把节点4入栈，接着遍历节点4的右子树。

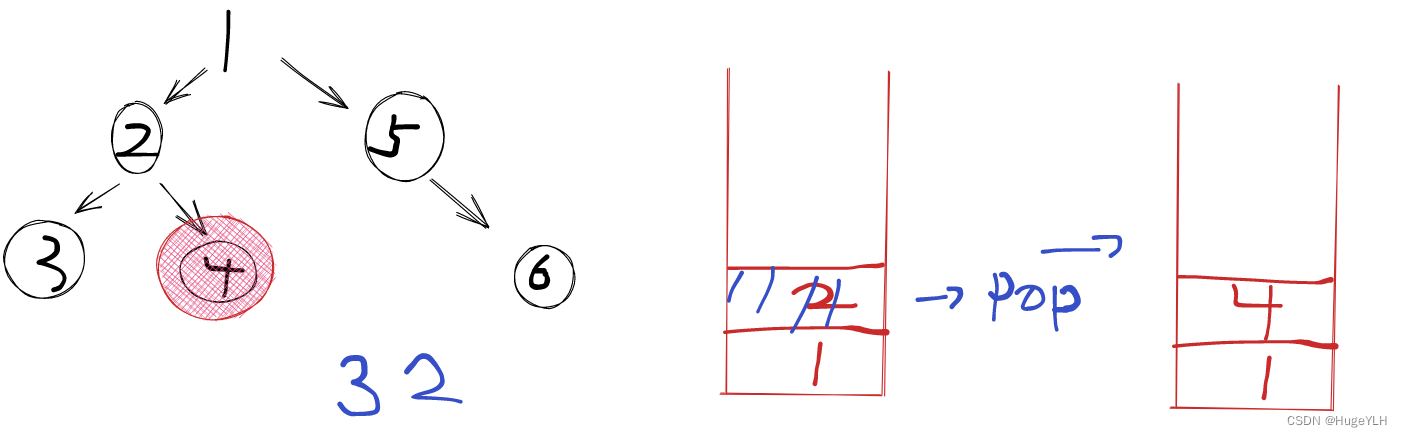
在这里插入图片描述
3. 节点4的右子树为空，弹出栈顶元素，弹出节点4，然后加入到res中，此时栈中只剩下了根节点1，弹出节点1，遍历根节点1的右子树，执行同样的操作。

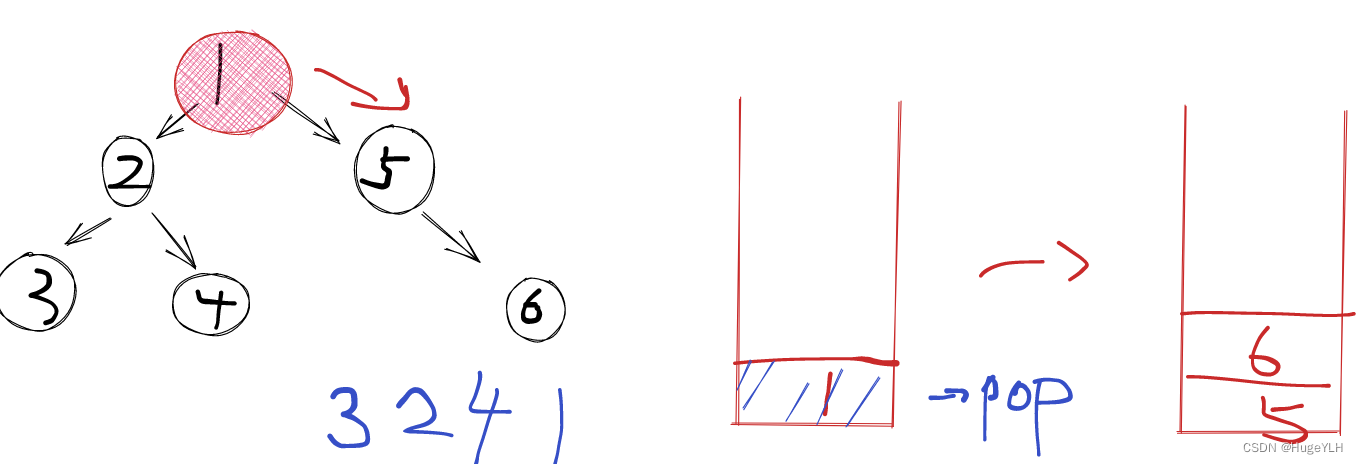
在这里插入图片描述

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> pstack;
        vector<int> res;
        while (root!=nullptr || !pstack.empty())
        {
            while (root!=nullptr)
            {
                pstack.push(root);
                root=root->left;
            }
            root=pstack.top();
            pstack.pop();
            res.push_back(root->val);
            root=root->right;
        }
        return res;
    }
};

线索二叉树解法

关于线索二叉树的原理及创建，可以看我这篇博客：
线索二叉树的创建解析

线索二叉树提供了无需递归便可以回到以前的节点的方法。
因为线索二叉树的左右指针保存了其当前节点的前驱节点与后继节点的指针，所以可以根据这个线索直接回到之前，不使用栈便可以实现这一操作。

具体实现：

当前节点 x 的左子树为空：将 x 添加到res中，x=x->right
当前节点 x 的左子树不为空：找到其左子树的最右端的节点，称作threadnode（当前左子树的中序遍历的最后的一个节点，这个节点即是x的left，然后一直往right，直到到达终点的那个节点）。
- threadnode的右指针为空，threadnode -> right = 当前节点x，x=x->left
- threadnode的右指针不为空，threadnode->right = nullptr，当前节点 x=x->right，x加入到res

图解：

x在根节点经过三次往左移动到达节点3的位置，同时进行了两次线索的连接：节点4右指针连接根节点；节点3右指针连接节点2。相当于保存了回去的位置。
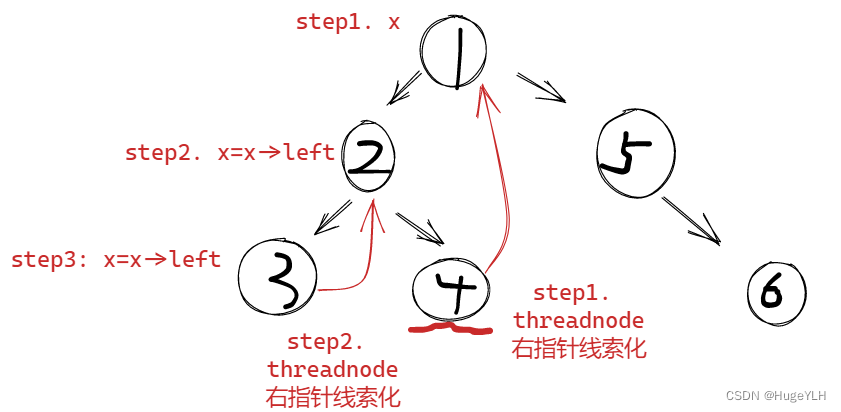
x此时位于节点3的位置，它的left等于空， 所以把x放入res中，x=x->right，x现在到了节点2的位置（由线索的right保存了节点2的位置）。紧接着再次找到节点2的左子树的最右节点threadnode，断开线索的连接，把x（当前是节点2）放入res中，然后继续遍历其右子树。
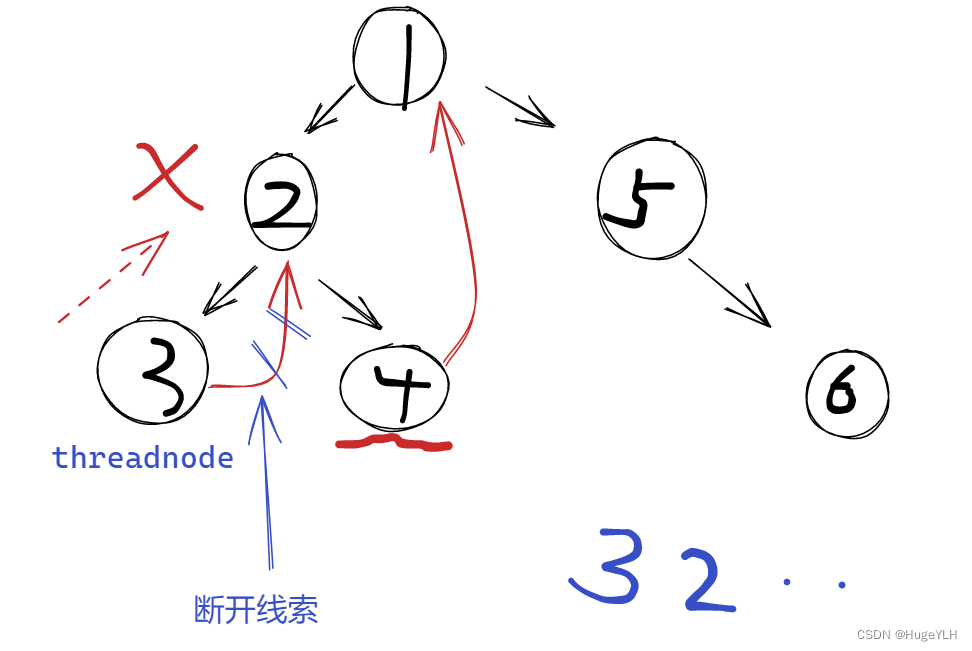
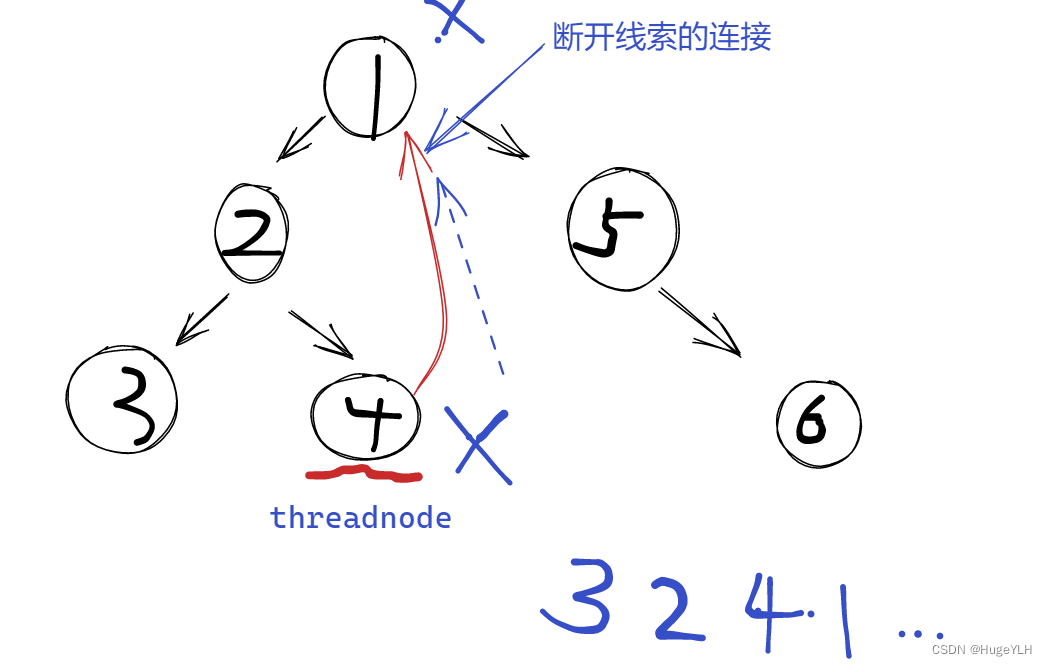
x到达节点4的位置，节点4的left为空，因此把节点4放入到res中，x=x->right（由threadnode右指针线索了原根节点的位置），所以x又回到了根节点1的位置；紧接着再次找到根节点1的左子树的最右节点threadnode，断开线索的连接，把x（当前位于根节点1）放入到res中，然后继续遍历右子树。。。。

代码示例：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        while (root!=nullptr)
        {
            if (root->left!=nullptr)
            {
            	//寻找每个节点对应的左子树的最右节点
                TreeNode* threadnode=root->left;
                while (threadnode->right!=nullptr && threadnode->right!=root)
                {
                    threadnode=threadnode->right;
                }
                if (threadnode->right==nullptr)
                {
                    //右指针线索化
                    threadnode->right=root;
                    root=root->left;
                }
                else
                {
                	//取消线索化
                    res.push_back(root->val);
                    threadnode->right=nullptr;
                    root=root->right;
                }
            }
            else
            {
            	//到达了某个具有线索的节点，存储与回溯
                res.push_back(root->val);
                root=root->right;   //保存的线索
            }
        }
        return res;
    }
};