然而，配电网的高效和安全运行涉及不同时间尺度的决策。[10]中提出了一种两阶段调度的动态规划方法：稳压器的抽头设置在较慢的时间尺度上，并在连续较短的时间段内保持固定，弹性负载被调度;然而，载荷的灵活性被认为是先验的。或者，集中计算的OPF决策可以在较慢的时间尺度上传达给公交车，而在较快的时间尺度上，光伏电力电子设备可以最佳地跟踪可再生能源发电和需求的变化[16]，[17]。依靠近似的电网模型，忽略了不确定性对慢响应机组调度的影响，后一种方案在快速响应机组之间产生了部分分散的电力流实时分配。

不确定性下的多级调度通常用于输电系统和微电网[18]。稳健的方法为最坏情况下的快速时间尺度结果找到最佳的慢时间尺度决策;见[19]及其中的参考资料。为了避免鲁棒方案的保守性，概率方法假设了需求、风力发电和系统突发事件的概率密度函数（pdf），以找到提前一天的电网时间表[20]，[21]。风险限制调度框架在接近实际时间[3]时，随着所涉及的随机变量的方差减小，调整多阶段决策。只有为了方便的网络约束风险限制调度和拥塞假设的pdfs，才能有效地计算决策[22]。作为第三种选择，样本平均近似（SAA）方法使用从假设的pdf中提取的样本产生最佳的慢时间尺度决策;见[19]、[23]。最近的工作对不良事件的概率施加了限制，要么依赖于机会约束的凸近似[24]，要么通过（基于样本的）场景近似方法[25]来减少计算;例如，[26]。

光伏逆变器以配电网为重点，可以在时间和总线上偶尔过载，以适应太阳能波动并防止过电压[27]。因此，电力系统组件（如逆变器、总线电压、线路流）的时空过载可能构成将可再生能源纳入智能电网的额外手段。尽管如此，确保过载的发生有节制地将决策与时间的耦合。[28]的单级方案可找到最佳的 PV 设定点，同时限制过载量的时间平均值。[29]中也采用了后一种方法，用于在减载的情况下提前一天/实时市场设置调度传输系统。

首先，第 III 节将两阶段电网调度表述为凸凹问题：在缓慢控制周期内的预期成本最小化，同时始终满足较宽松的电压限制，并在平均或在概率上。其次，根据[30]中的随机鞍点近似方案，第四节中的可证明收敛算法为平均约束公式提供了最佳的慢时间尺度决策。与 SAA 方法不同，这种随机近似 (SA) 方案一次处理一个随机样本以提高计算效率。第三，在非凸概率约束的情况下，在第五节中提出了一种解决每个第二阶段的两个相似凸问题的算法。虽然预期成本享有零对偶差距[31]，但总体两阶段调度是不是凸凹的，这就解释了为什么算法的性能是通过数值验证的。两种方案都只需要负载和太阳能发电的样本，并且可以依赖于近似或凸网格模型。在 56 和 123 节点上使用线性化分布流模型的数值测试证实了我们在第 1 节中发现的有效性。

2 数学模型 

详细数学模型见第5部分。

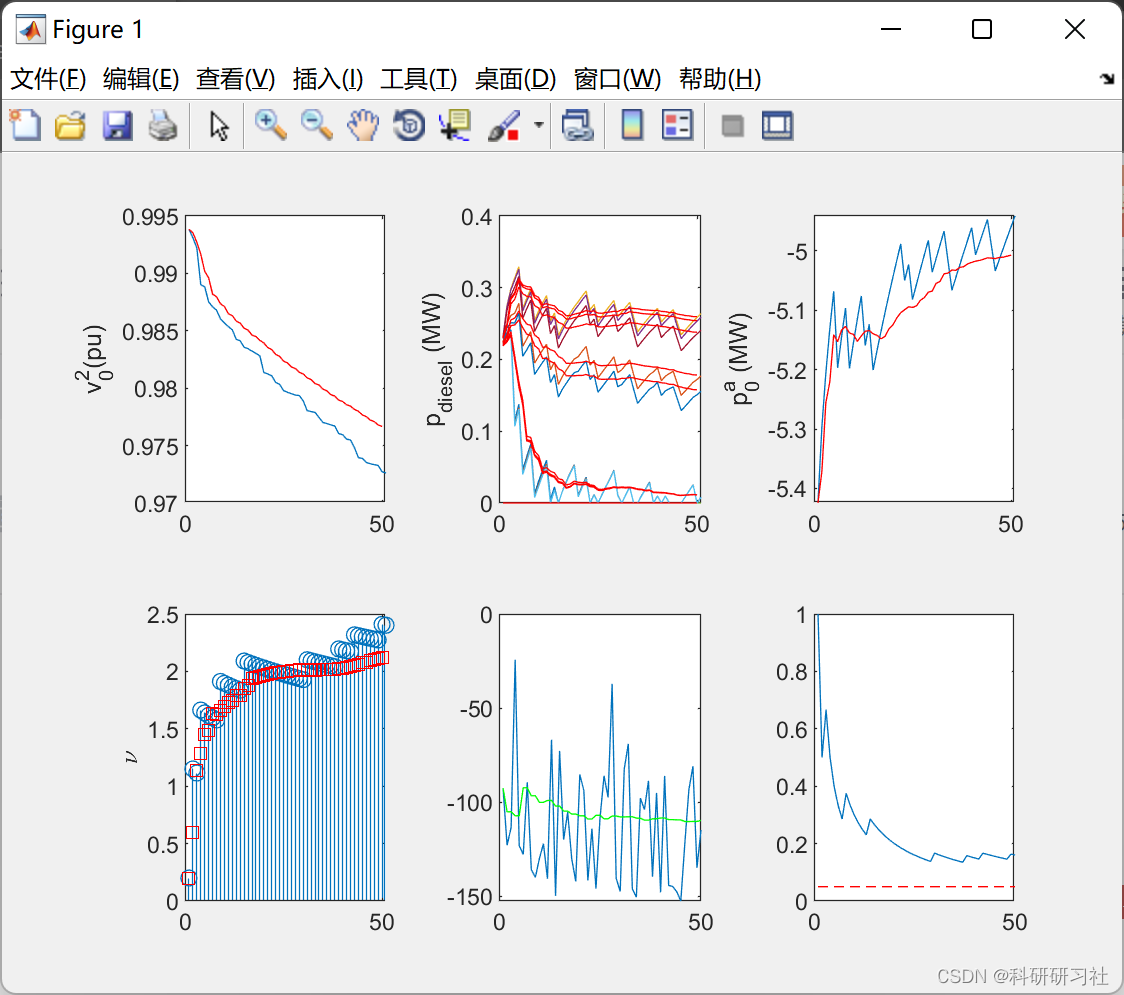
 3 运行结果

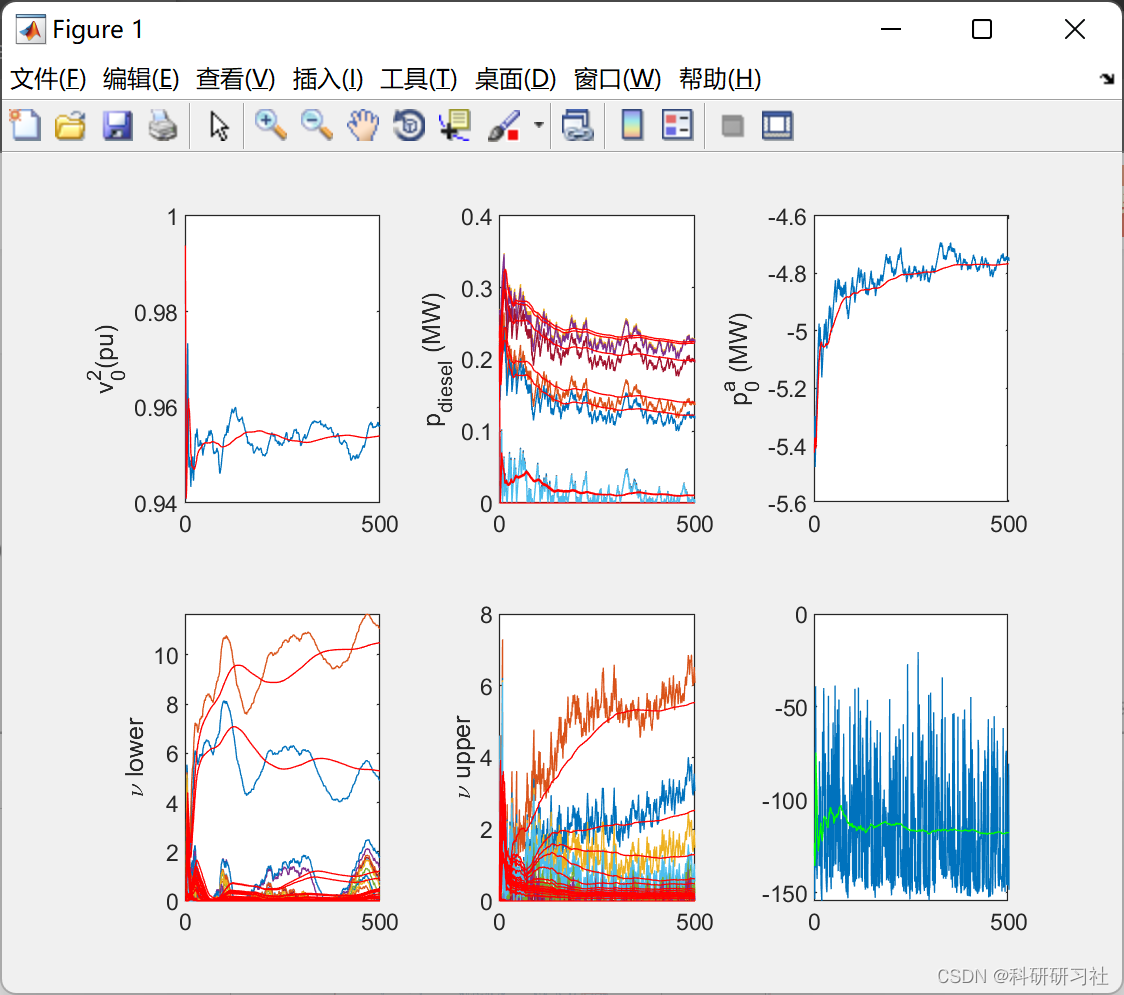
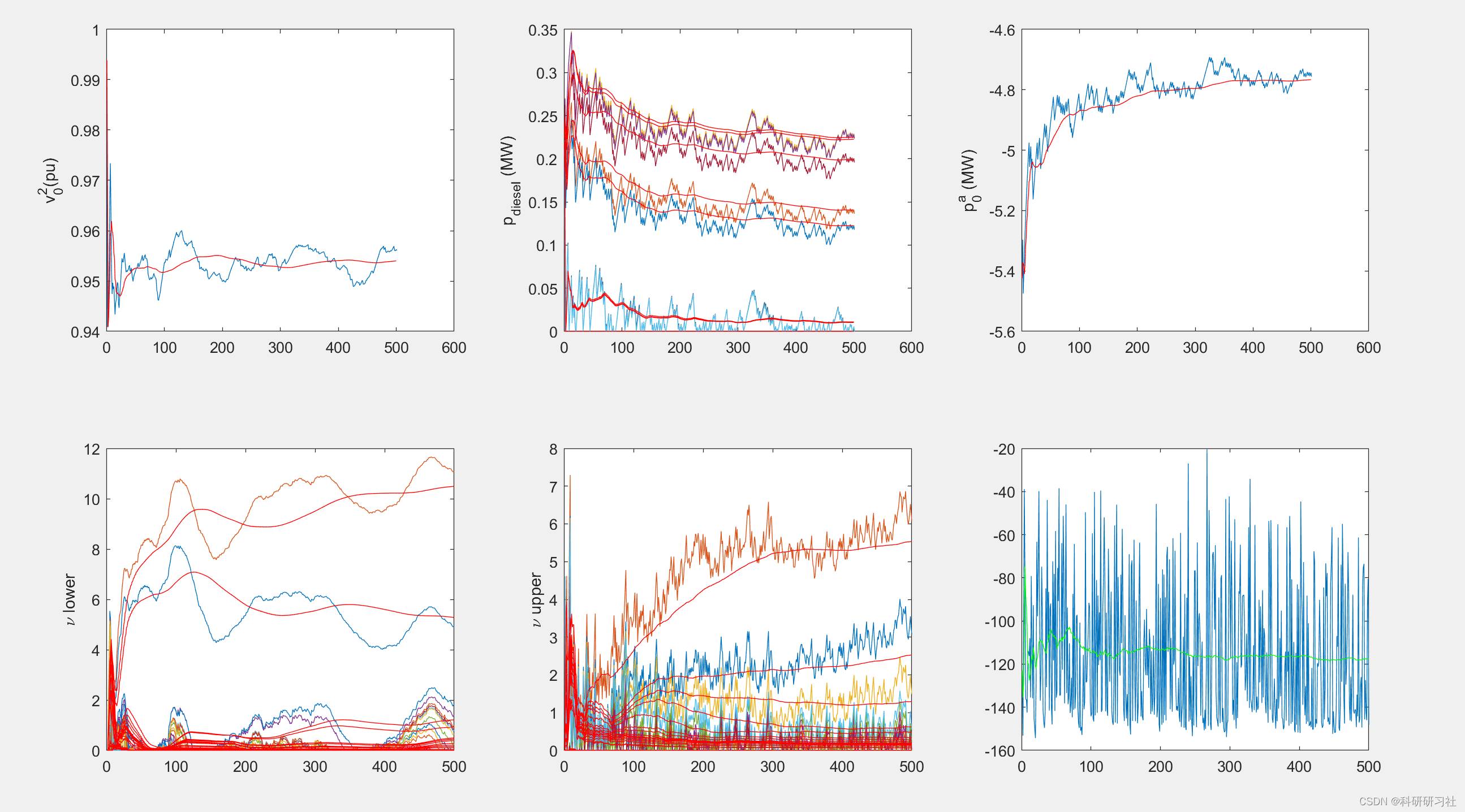
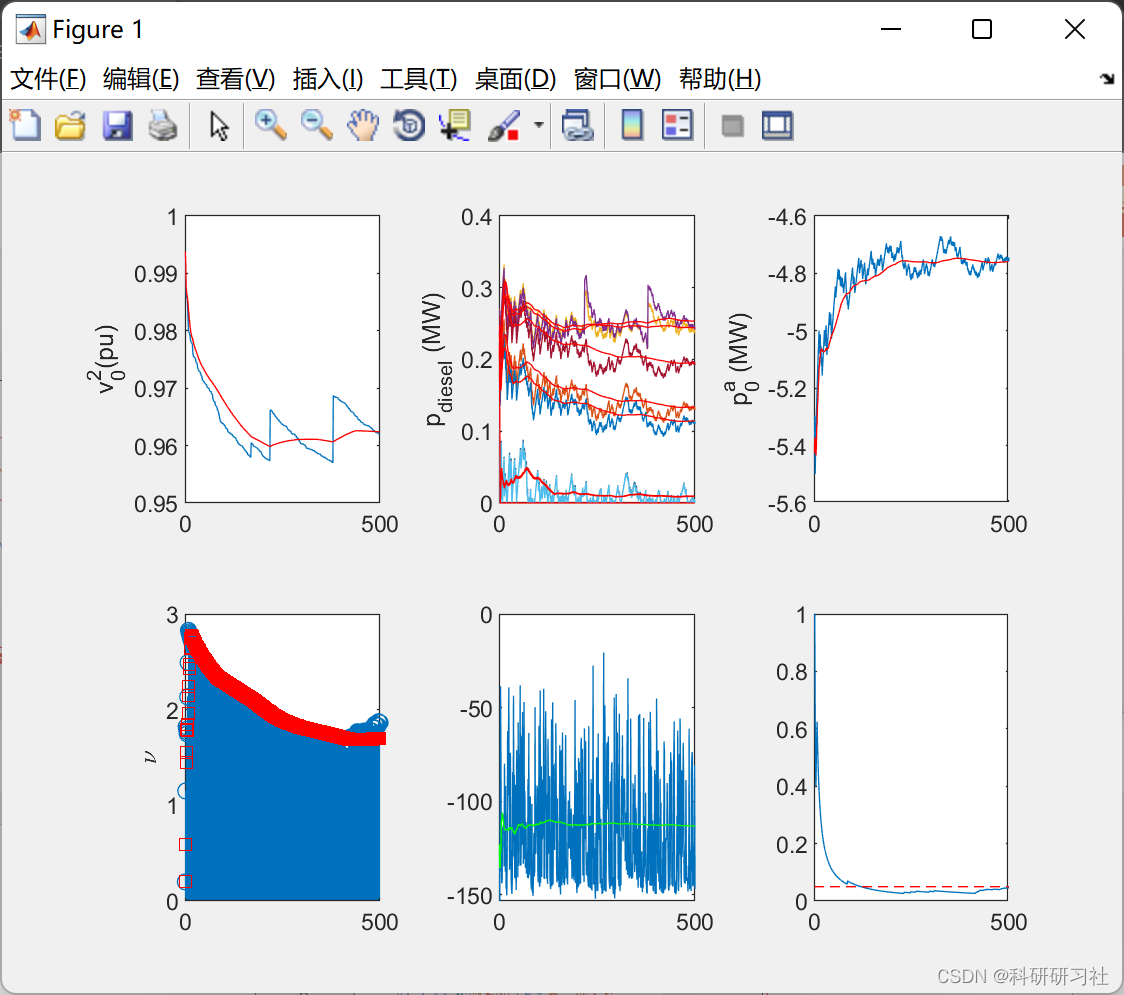
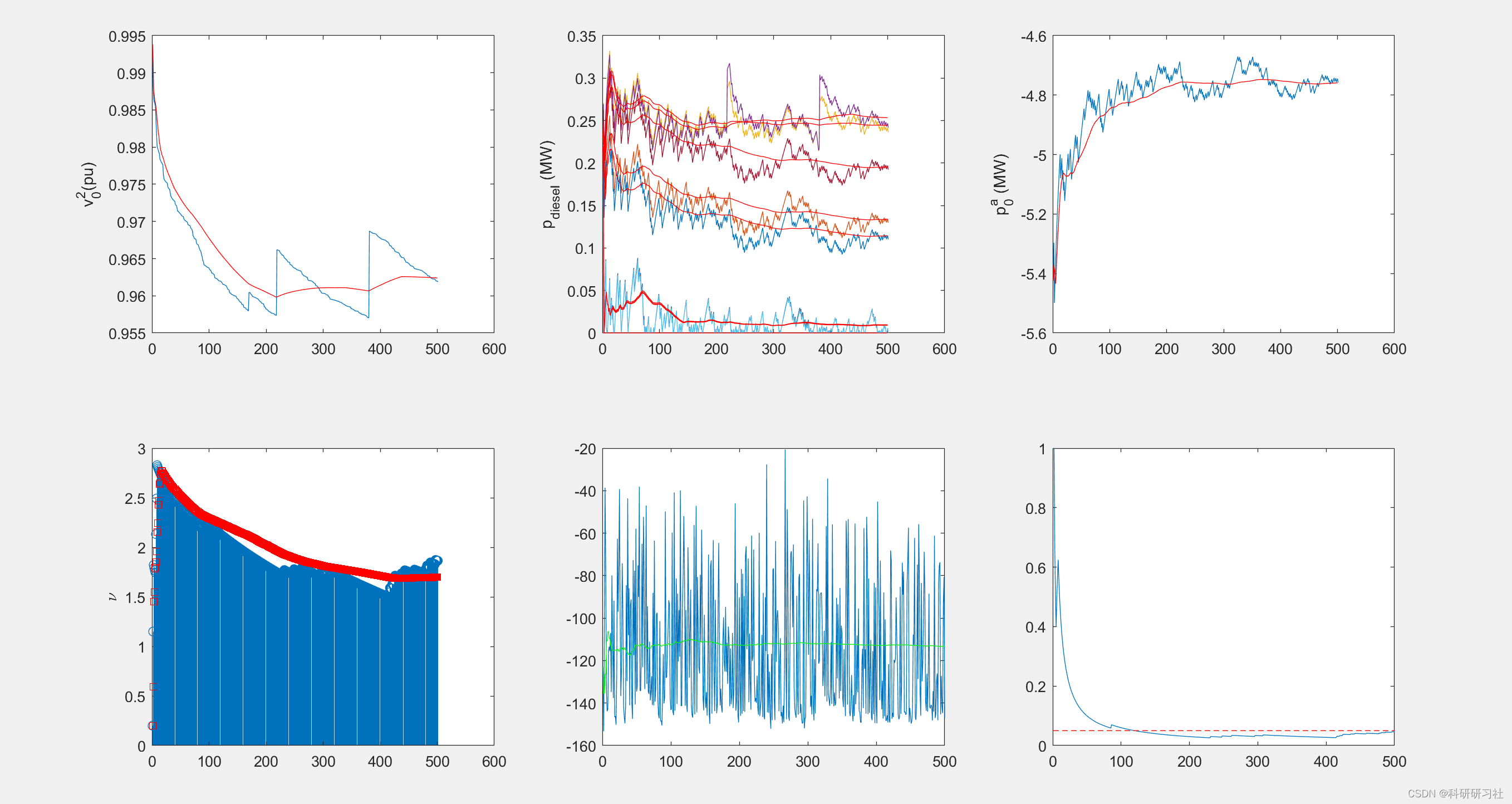
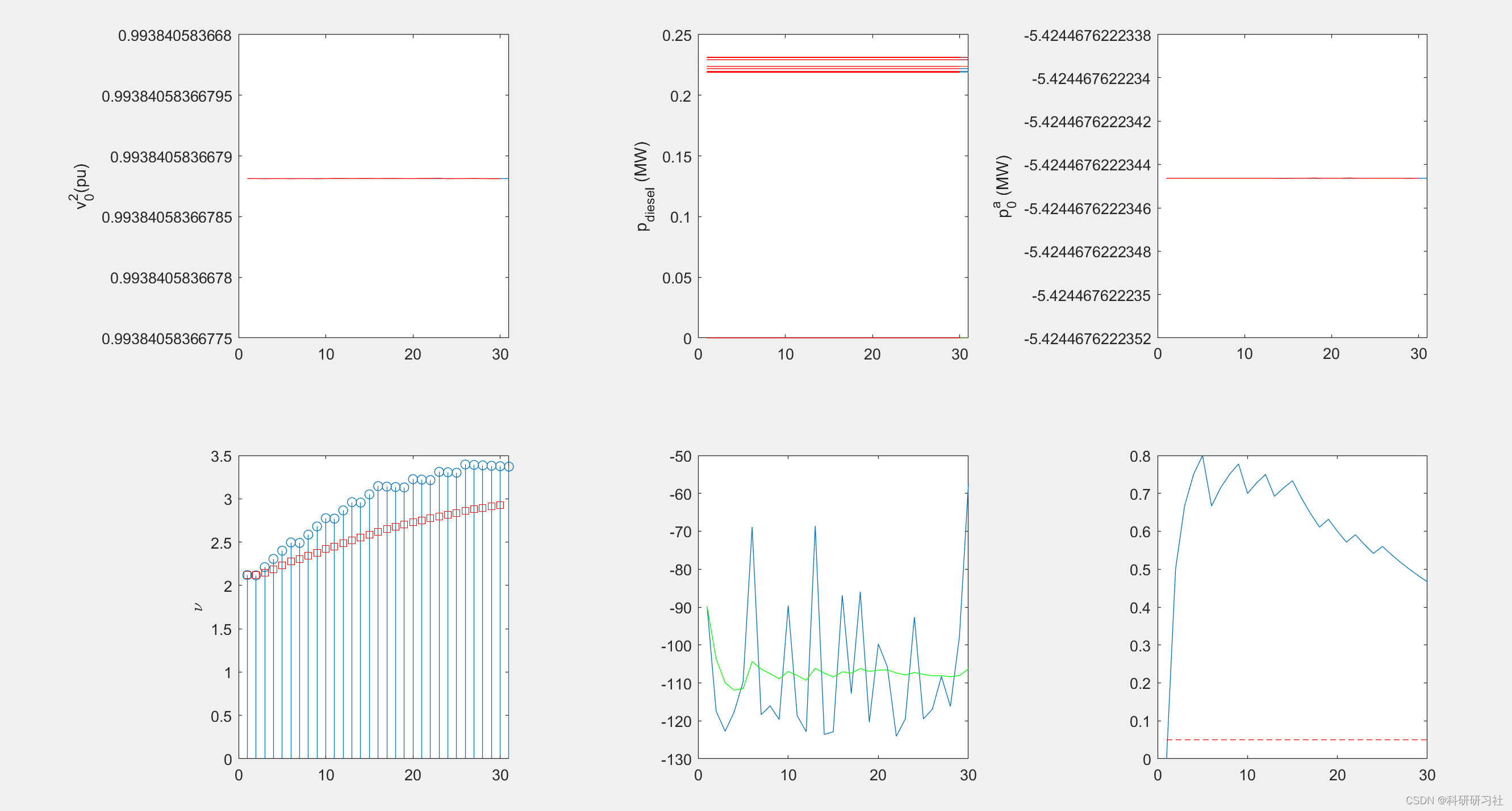
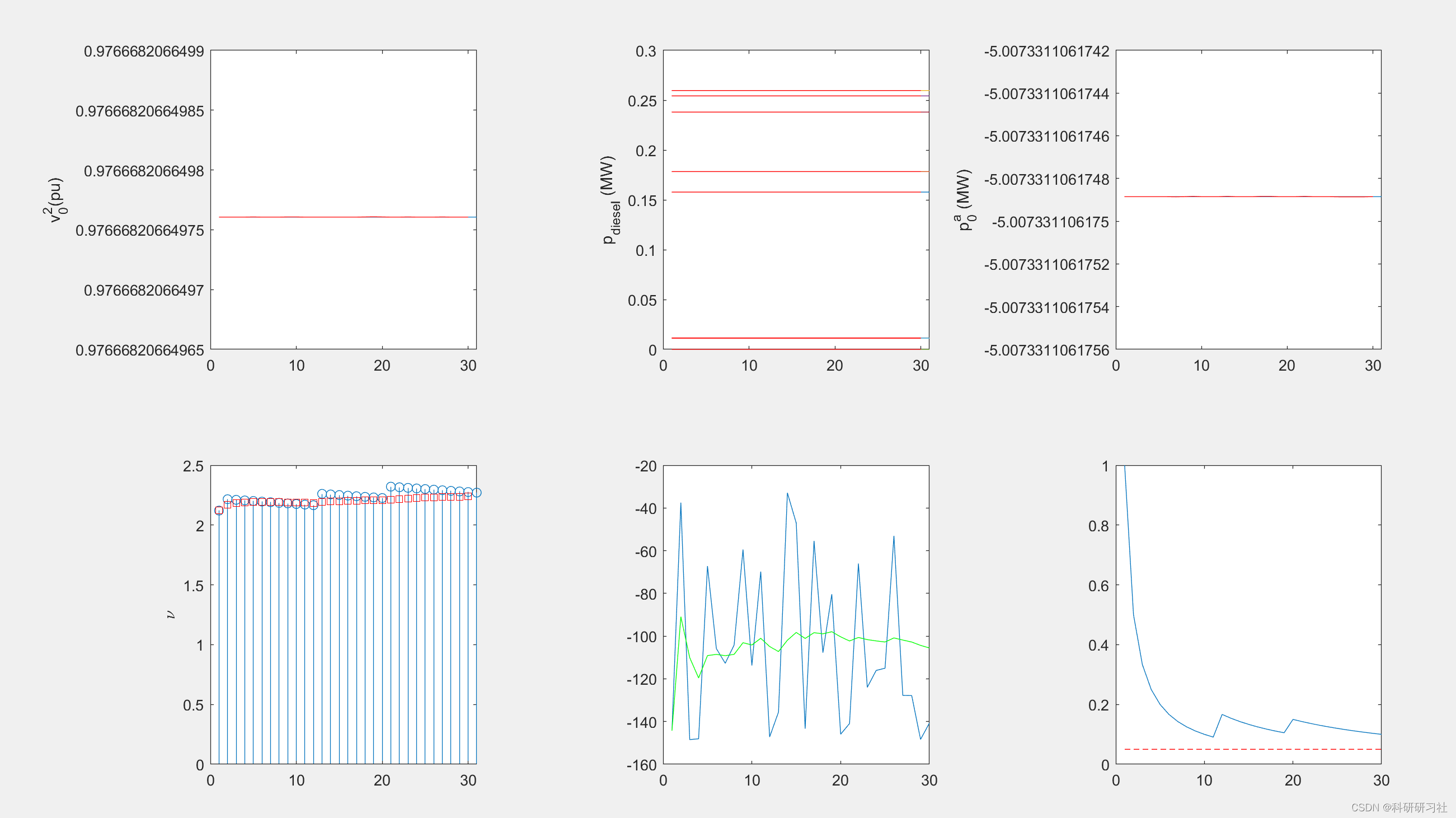
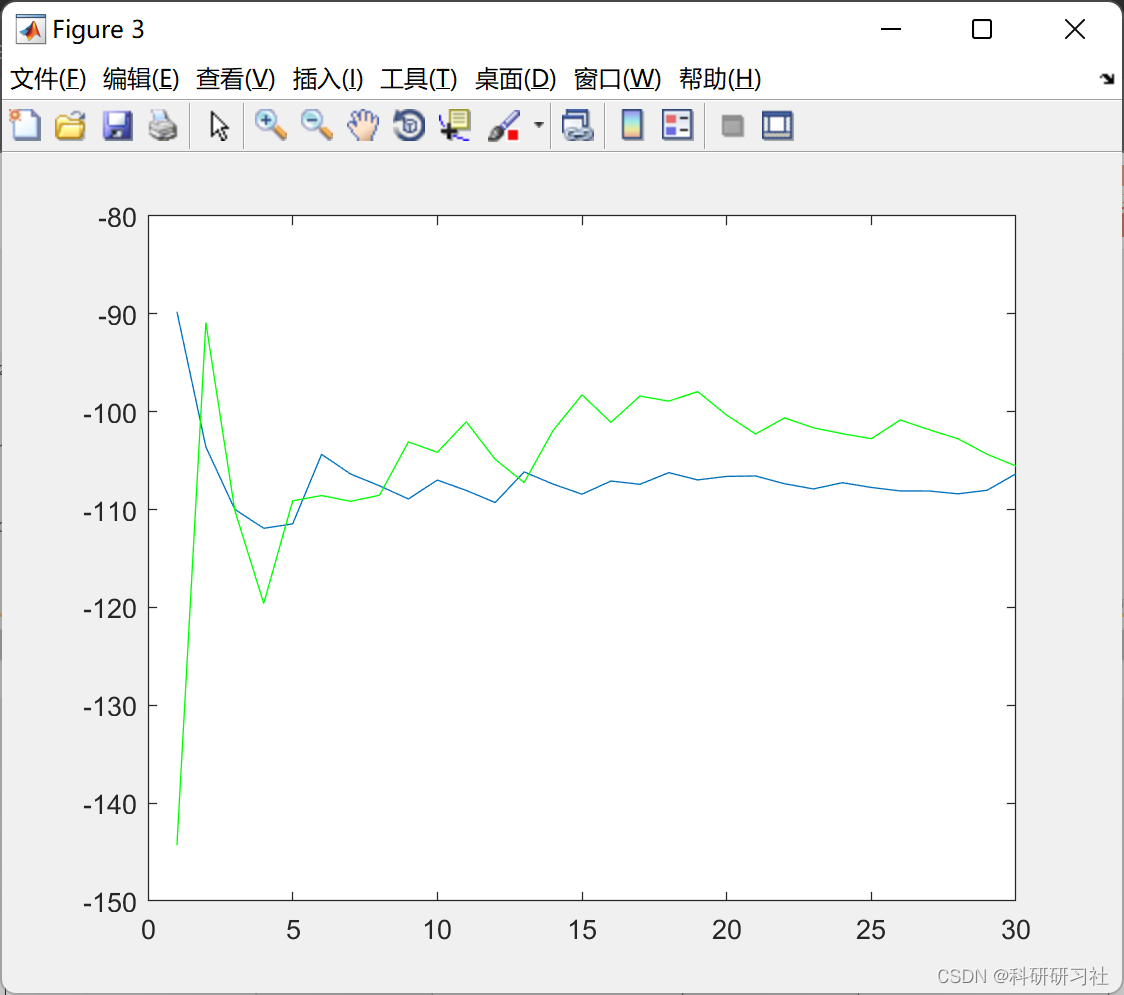
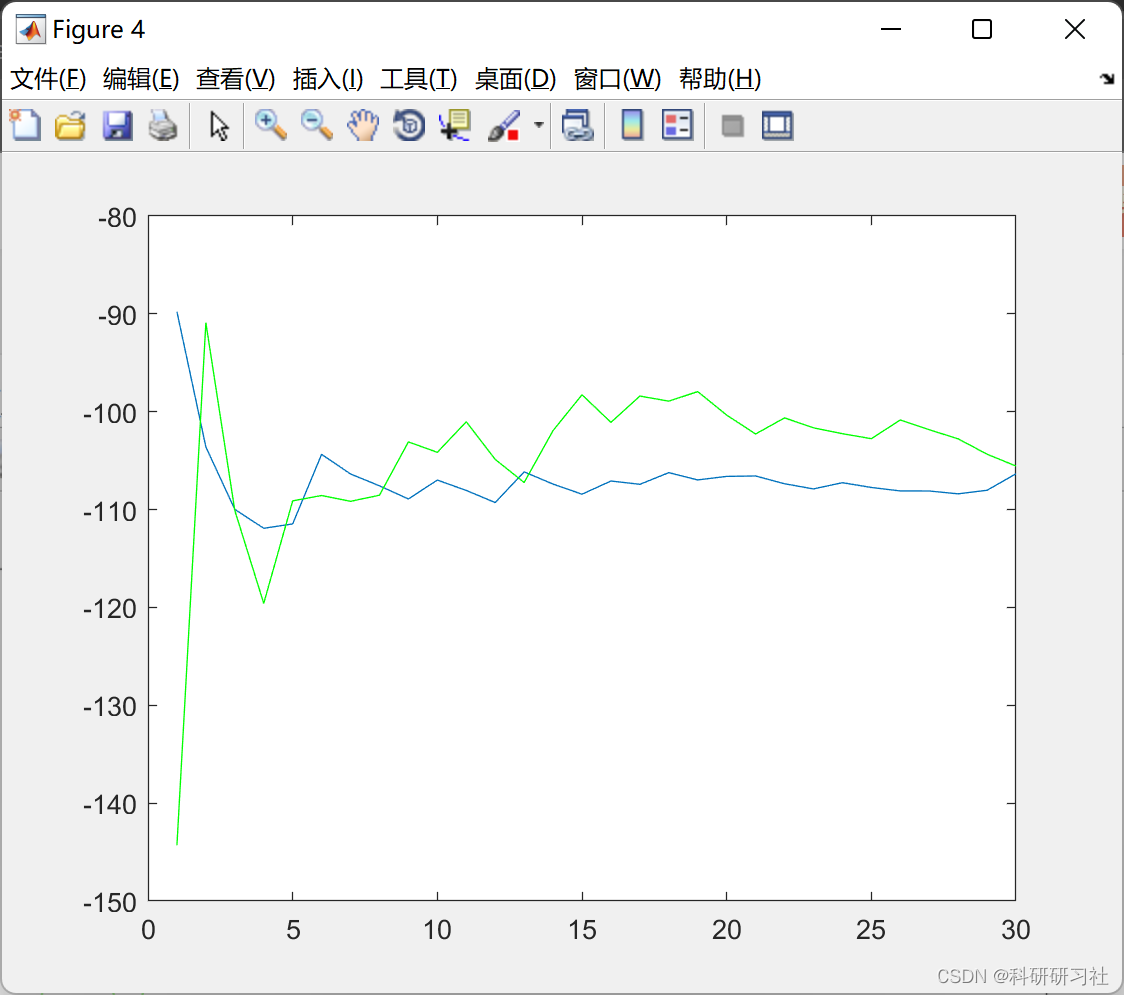
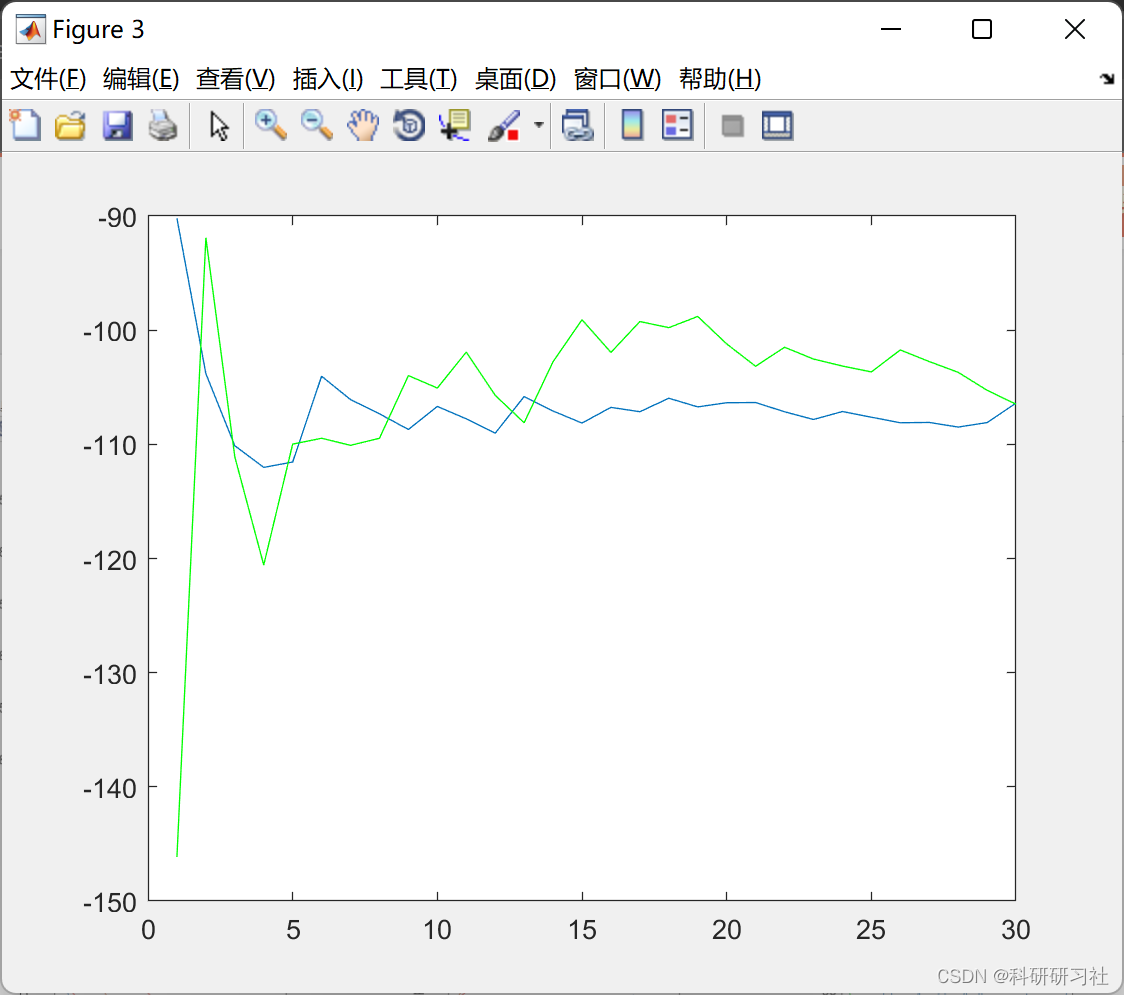
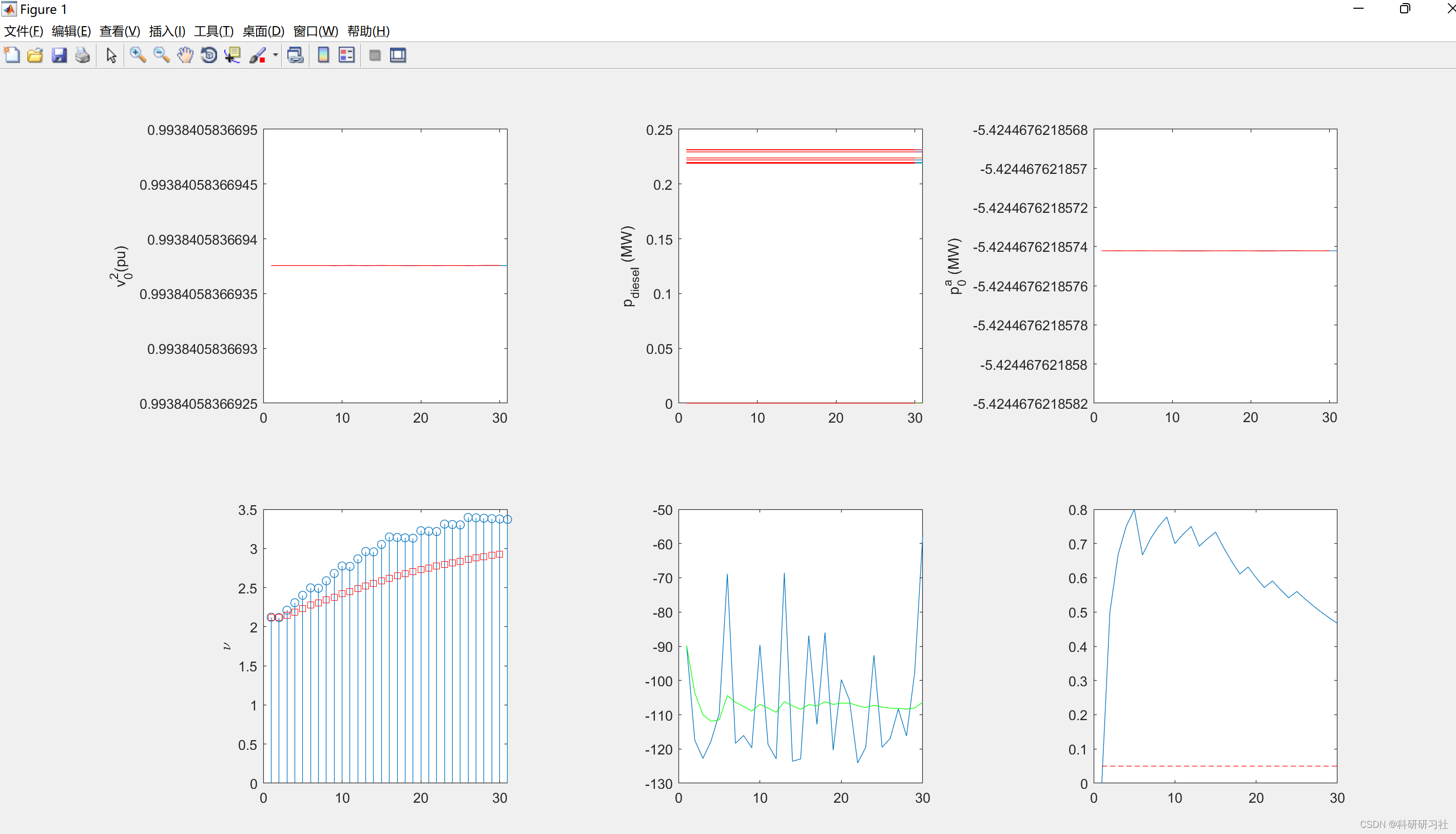
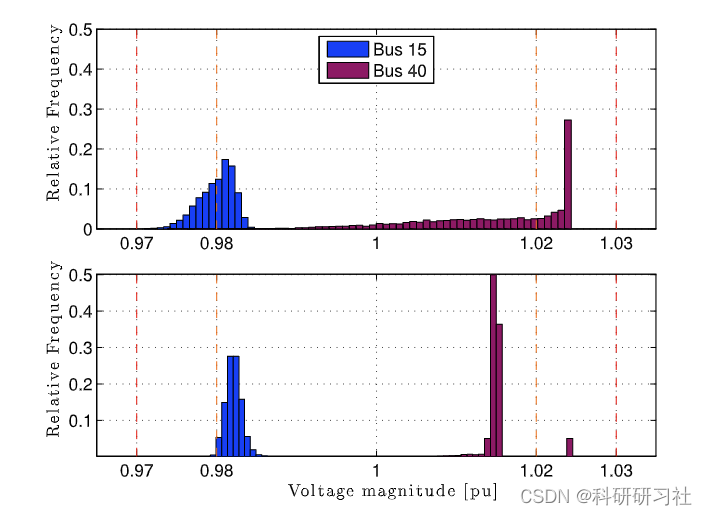
 4 结论

由于可再生能源发电的性质、机电组件的限制以及市场运作的方式，智能配电网的能源管理涉及越来越慢的时间尺度的决策。由于慢时间尺度控制在多个 PV 操作时隙上保持固定，因此决策以随机方式跨时间耦合。为了适应太阳能的波动，电压被允许偶尔过载。因此在平均或概率上引入了快速时间尺度变量的耦合。平均电压约束导致随机凸凹问题，而非凸概率约束通过对偶分解和凸优化来解决。已经提出了仅使用随机样本来查找慢速和快速控制的有效算法。我们的两个新求解器在原始变量和对偶变量方面收敛，并且与确定性替代方案相比获得了更低的运营成本。虽然概率约束已按网格应用，但个别总线上的电压仍保持在限制范围内。在每条总线的基础上实施概率约束、开发分散的实现以及包括电压调节器是有趣的研究方向。

5 参考文献

部分理论引用网络文献，如有侵权请联系删除。

[1] Lopez-Ramos L M ,  Kekatos V ,  Marques A G , et al. Two-Timescale Stochastic Dispatch of Smart Distribution Grids[J]. IEEE, 2018(5).

6 Matlab代码实现

博客主页：电气辅导帮