07 Sigmoid
使用类DBSCAN的思路对轨迹聚类
1 intro
1.1 轨迹聚类
- 现有的轨迹聚类算法是将相似的轨迹作为一个整体进行聚类,从而发现共同的轨迹。
- 但是这样容易错过一些共同的子轨迹(sub-trajectories)。
- 而在实际中,当我们对特殊感兴趣的区域进行分析时,子轨迹就特别重要。
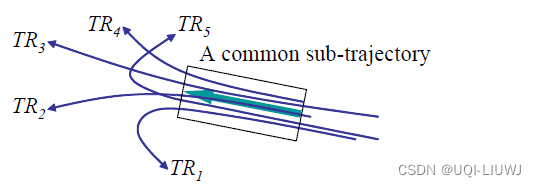
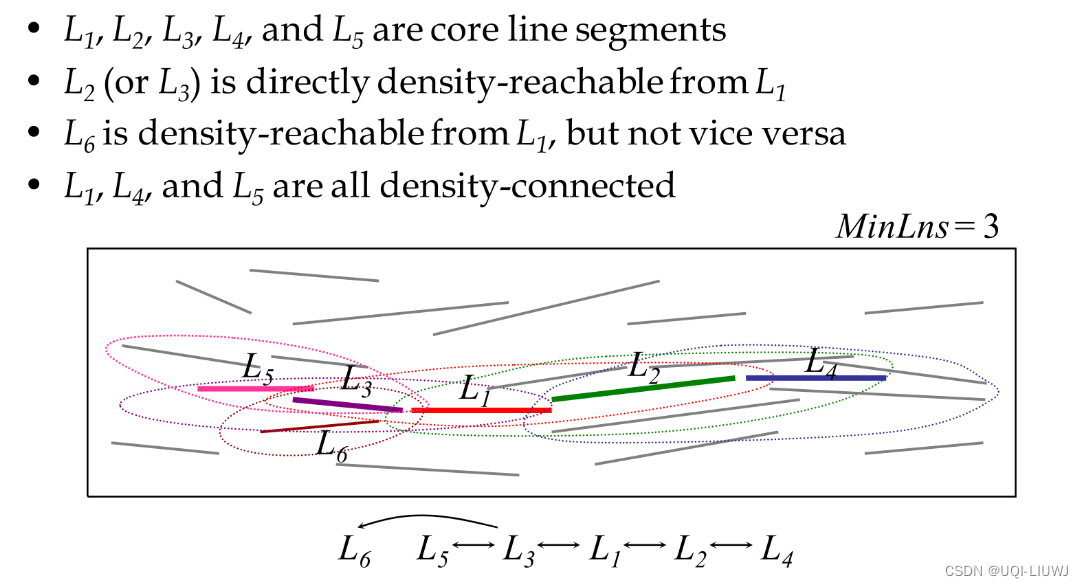
- 图中有五条轨迹,在矩形中有一个共同的行为,用粗箭头表示。
- 如果我们将这些轨迹作为一个整体来聚类,我们就无法发现共同的行为,因为它们最终向完全不同的方向移动
- ——》作为一个整体来聚类会错过很多有价值的信息。
1.2 本文的思路
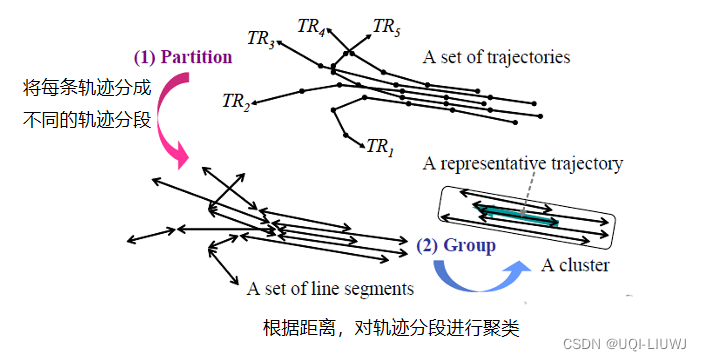
- 本文提出TRACLUS算法,先将轨迹分段成线段,然后再对线段进行聚类,可以更准确地发现子轨迹。
- 算法步骤分为分段(partitioning)和归组(grouping)
- 分段利用最小描述长度(minimum description length MDL)原理实现轨迹分段,将每一条轨迹最优的分为一组线段,这些线段输入到下一阶段。
- 归组利用基于密度的线段聚类算法实现相似线段聚类。设计了一个距离函数来定义线段的密度。
- ——>基于密度的聚类方法是最适合用于线段的,因为它们可以发现任意形状的聚类,并可以滤波出噪声。可以很容易地看到,线段簇通常是任意形状的,而轨迹数据库通常包含大量的噪声
2 问题定义
- 输入一组轨迹
- 一条轨迹是一组点的集合
,其中每一个点pj是一个d维的点(坐标),leni是这条轨迹的长度(点的数量)
- 轨迹TRi的一条子轨迹是
- 一条轨迹是一组点的集合
- 输出:一组线段聚类
和每个线段聚类Ci的代表性轨迹
- 一个cluster中是一组轨迹分段
- 一个轨迹分段是一条线段
,其中pi和pj都是从同一条轨迹中选择的点
- 一个轨迹分段是一条线段
- 一条轨迹中的轨迹分段可能属于不同的多个聚类
- 一个cluster中是一组轨迹分段
3 模型
3.1 整体模型
3.2 轨迹距离函数
- 对点集做聚类时,常用方法就是根据两点之间的欧氏距离来判断是否一类。
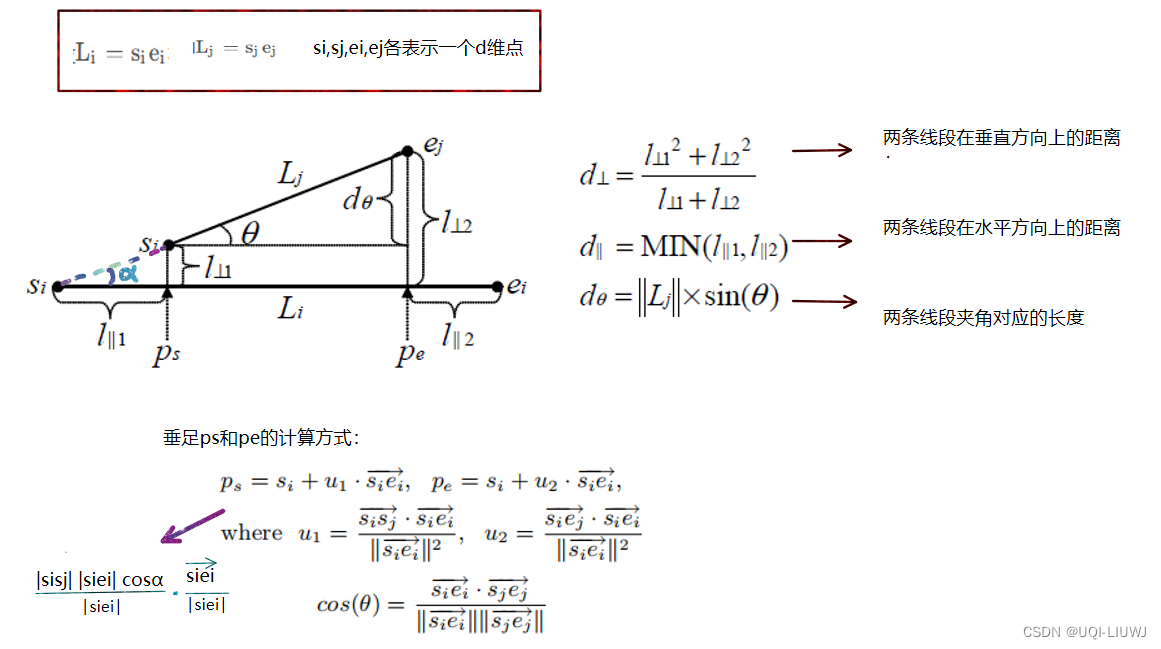
- 在线段聚类时,论文使用的距离函数是由三个部分组成
- 垂直距离
- 平行距离
- 角度距离
- 垂直距离

3.2 轨迹分段
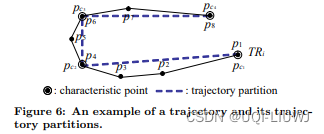
- 轨迹分段的首要目标是找到轨迹行为迅速变化的点(就是角度变化大的点),称之为特征点。
- 从轨迹
中确定了一组特征点
- 然后轨迹TRi分每个特征点分段,每个分段用两个连续特征点所连的线段表示
- ——>TRi被分成一组(pari-1)个轨迹分段
- 从轨迹
3.2.1 轨迹分段原则
- 一个轨迹的最优分段要具有两个属性:
- 准确性
- 轨迹与其一组轨迹分段之间的差异应该尽可能小
- ——>特征点不能太少。
- 轨迹与其一组轨迹分段之间的差异应该尽可能小
- 简洁性
- 轨迹分段的数量应该尽可能少
- 准确性
- 这两个属性在确定特征点数目时是相互矛盾的,这就需要调整算法以达到平衡
3.2.2 最小描述长度原则(Minimum Description Length,MDL)
- 最小描述长度( MDL) 原理是通用编码领域研究的内容。
- 基本原理是对于一组给定的数据 D ,如果要对其进行保存 ,为了节省存储空间, 一般采用某种模型对其进行编码压缩,然后再保存压缩后的数据。
- 同时, 为了以后正确恢复这些实例数据,将所用的模型也保存起来。
- ——>所以需要保存的数据长度( 比特数) 等于 数据进行编码压缩后的长度 加上 保存模型所需的数据长度,将该数据长度称为总描述长度。
- 最小描述长度( MDL) 原理就是要求选择总描述长度最小的模型
- MDL的代价有两部分L(H)和L(D|H)
- H代表压缩模型,D代表数据
- L(H)是描述压缩模型(或编码方式)所需要的长度
- L(D∣H)是描述利用压缩模型所编码的数据所需要的长度
- 类比到轨迹分段中,如下:
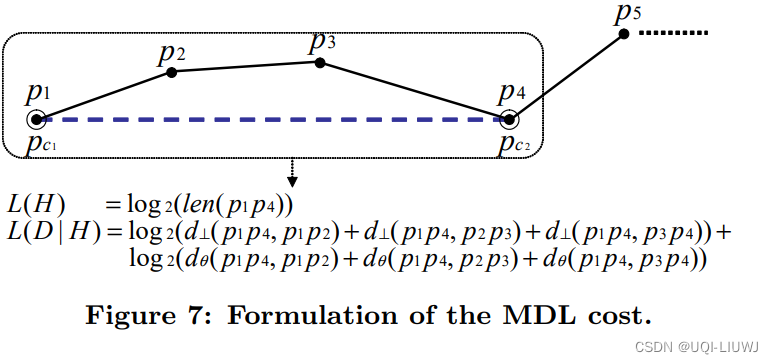
- L(D|H)只考虑角度距离和垂直距离,不考虑平行距离
-
假设一条轨迹
,一组特征点
-
L(H)表示为
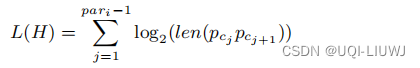
-
L(D|H)表示为:
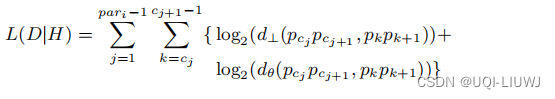
——>因此,要得到最优的分段策略,那就是要最小MDL= L(H)+L(D|H),这能够准确平衡简洁性和准确性
-
3.2.3 近似计算方法
- 但是因为要考虑到轨迹点的每一个子集,所以计算量是非常大
- 论文引入一个近似计算的方法,关键思想是将局部最优的集合视为全局最优
- 记
表示pi和pj是 路径分段pipj之间仅有特征点时(也就是pipj之间的子线段都划归到pipj线段上了),pipj二者之间轨迹的MDL
- 记
表示pi和pj之间没有特征点时的MDL
- 此时pipj之间就是原始轨迹,所以只有L(H),没有L(D|H)
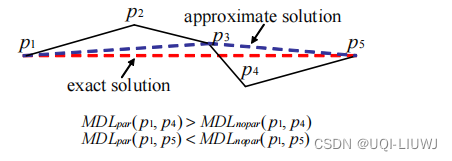
- 局部最优解是:当满足对于任意i<k≤j的k,都有
时的最长pipj
- 不等式的意思是:pi~pk的点,视作pipk轨迹分段对应的MDL,比pipk的点保持为原始轨迹对应的MDL小
- 也就是说pipk是一个最优分段
- 换句话说就是pk作为特征点的MDL比不作为特征点的代价小,那么pk可以成为一个特征点
- 局部最优解找的就是距离i最远的、可以作为特征点的点j
- 不等式的意思是:pi~pk的点,视作pipk轨迹分段对应的MDL,比pipk的点保持为原始轨迹对应的MDL小
算法如下
所以此时p4就是局部最优解
3.3 聚类
3.3.1 基于密度聚类的概念
将DBSCAN中关于点的聚类扩展到关于线段的聚类
- 几个notation:
- D是所有线段的集合
- epsilon是两个线段距离的一个阈值
- MinLns是聚类集合的最小线段数量
| 线段 |
|
| 核心线段 |
核心线段就是,和线段Li相距小于ε的线段数量 大于MinLns条
|
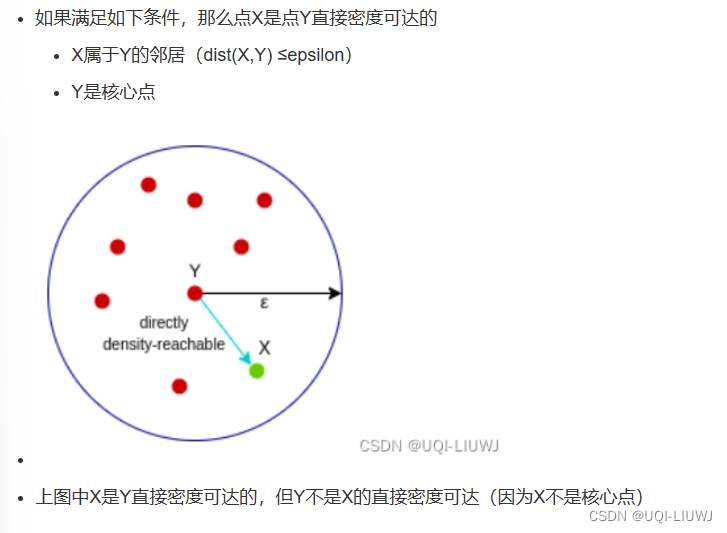
| 直接密度可达 | Lj是核心线段+Li在Lj的ε邻域内——>Li直接密度可达Lj
|
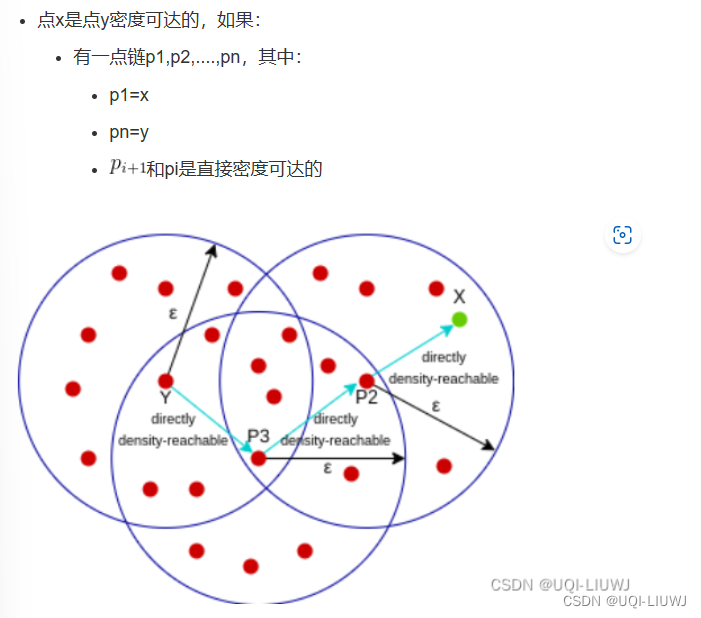
| 密度可达 | 存在一组线段 其中Lk直接密度可达 那么Li密度可达Lj
|
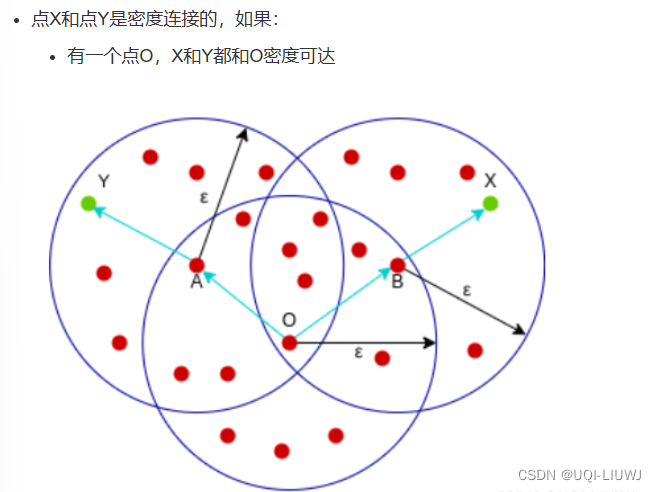
| 密度连接 | 当存在一个核心点Lk,使得线段Li和线段Lj都密度可达Lk 那么Li 密度连接Lj
|
3.3.2 密度连接集

3.3.3 线段聚类方法
- 有别于DBSCAN的就是14~16行,即并非所有的密度连接集都是一个线段聚类
- 需要考虑这一簇的线段是从几条轨迹中得来的,如果小于阈值,那么这一簇线段不能被视为一个聚类
- 举一个极端情况,一个簇中所有的线段都是从一个轨迹中提取出来的
- ——>14~16行就是校验一个簇中轨迹的基数
- 需要考虑这一簇的线段是从几条轨迹中得来的,如果小于阈值,那么这一簇线段不能被视为一个聚类
3.3.4 聚类算法的扩展
- 每条线段可以有自己的权重
- ——>此时可以修改 确定ε邻域基数
的方法,不再是简单地计算线段数量,而是计算线段的加权数量
- ——>此时可以修改 确定ε邻域基数
参考内容:
GPS轨迹聚类算法TRACLUS介绍(一)_NieBP的博客-CSDN博客
GPS轨迹聚类算法TRACLUS介绍(二)_traclus-master_NieBP的博客-CSDN博客
GPS轨迹聚类算法TRACLUS介绍(三)_NieBP的博客-CSDN博客
GPS轨迹聚类算法TRACLUS介绍(四)_NieBP的博客-CSDN博客

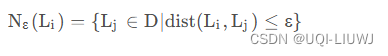
 ,mn
,mn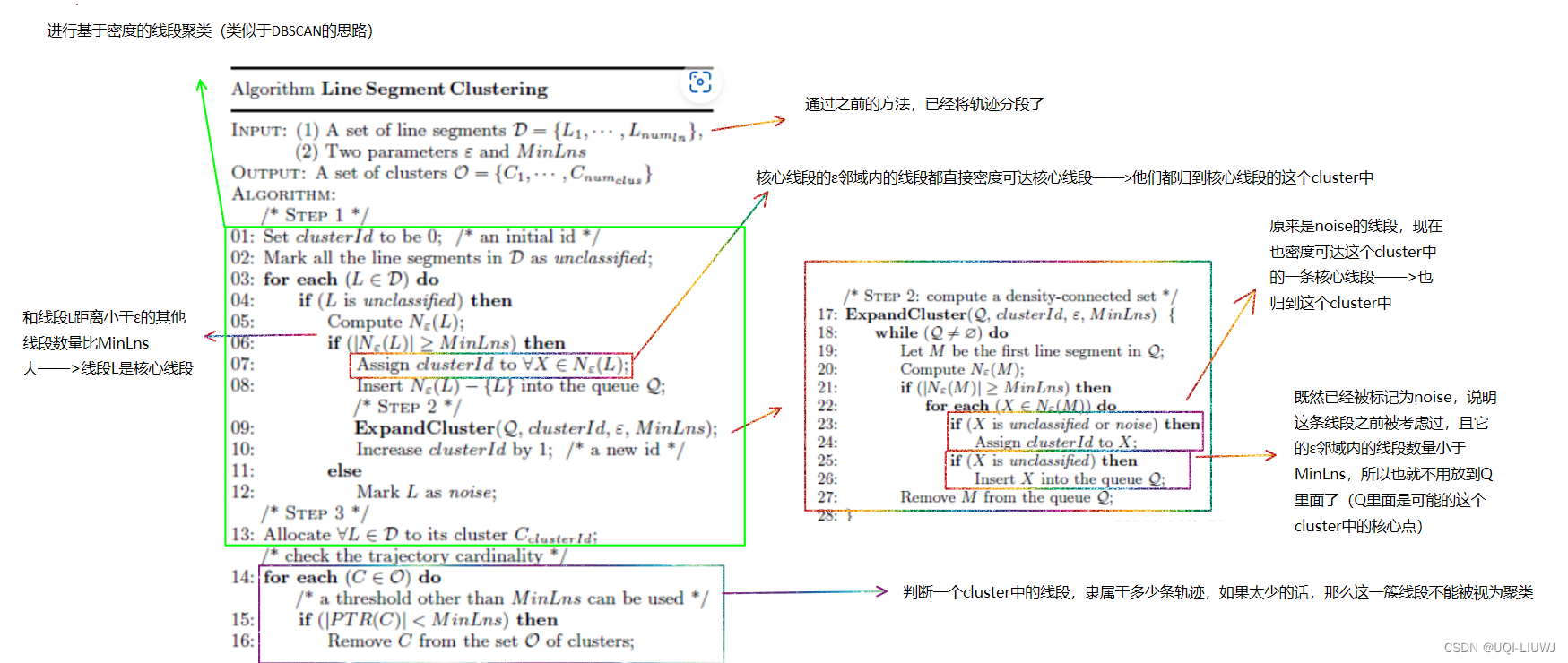








![[PCIE733]基于PCI Express总线架构的2路160MSPS AD采集、12路LVDS图像数据采集卡](https://img-blog.csdnimg.cn/202e0ece6fb44da891231c90eb4a014f.png)
![【dfs序+线段树】P3178 [HAOI2015]树上操作](https://img-blog.csdnimg.cn/320dc6c5e426487da59967c53466e949.png)