题目描述

法一）二分查找

与搜索二维矩阵——力扣74不同，本题没有保证「每行的第一个整数大于前一行的最后一个整数」，因此无法采取「两次二分」的做法

• 退而求之，遍历行/列，然后再对列/行进行二分。

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m=matrix.size(), n=matrix[0].size();
        for(int i=0;i<m;i++){
            int l=0, r=n-1;
            while(l<r){
                int mid=(l+r+1) >> 1;
                if(matrix[i][mid] <= target) l=mid;
                else r=mid-1;
            }
            if(matrix[i][r] == target) return true;
        }
        return false;
    }
};

//另一种写法
class Solution{
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target){
        int n=matrix[0].size();
        for (const auto& row : matrix){   //const auto& 表示只读取matrix中的元素，不修改
            int l=0, r=n-1;
            while(l<r){
                int mid=(l+r+1) >> 1;
                if(row[mid]<=target) l=mid;
                else r=mid-1;
            }
            if(row[r]==target) return true;
        }
        return false;
    }
};

复杂度

• 时间复杂度O(mlog n) 或O(nlog m)
• 空间复杂度O(1)

法二）抽象二叉搜索树BST

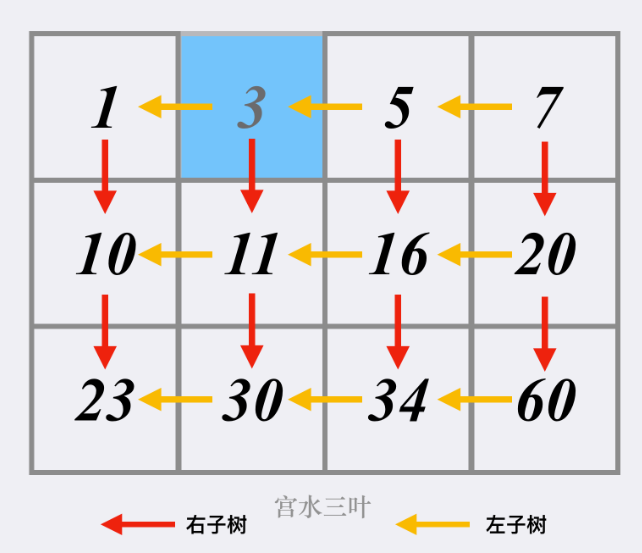
同搜索二维矩阵——力扣74中的法三）完全一致，将二维矩阵抽象成「以右上角为根的 BST」：

那么可以从右上角开始搜索，若当前值不等于目标值，按照树的搜索顺序进行：
若当前值「大于」目标值，则搜索当前节点的「左子树」，即j–；
若当前值「小于」目标值，则搜索当前节点的「右子树」，即i++；

class Solution{
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target){
        int m=matrix.size(), n=matrix[0].size();
        for (int i=0, j=n-1;i<m & j>=0;){
            if(matrix[i][j]==target) return true;
            else if(matrix[i][j]>target) j--;
            else i++;
        }
        return false;
    }
};

复杂度

• 时间复杂度O(m+n)
• 空间复杂度O(1)

法三）直接查找

直接遍历整个矩阵matrix，判断target是否出现

class Solution{
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target){
        for (const auto& row : matrix){
            for (int col : row){
                if(col == target) return true;
            }
        }
        return false;
    }
};

复杂度

• 时间复杂度O(m*n)
• 空间复杂度O(1)